基于全调节RBF神经网络的引信噪声对消研究
2012-12-03李国林路翠华
李 静, 李国林, 路翠华
(海军航空工程学院战略导弹工程系,山东 烟台264001)
0 引言
在严重的电子干扰和环境背景干扰条件下,从被噪声污染的回波信号中提取真实的目标信号是引信信号处理领域中一个重要的问题。通常的方法是采用自适应噪声抵消器来实现[1-4]。它利用与噪声相关的信号来调整滤波参数,实现对噪声的抑制,其算法很多,如最小均方(least mean square,LMS)算法、牛顿算法等。但由于引信对干扰源特征未知,干扰噪声的传递路径不断变化,回波信号中包含的干扰噪声具有非线性的变化规律,因此实现对干扰噪声的最优滤波需要采用非线性的自适应算法。由于全调节RBF神经网络具有处理非线性参数的不确定性,提高了神经网络的在线逼近能力。因此,本文针对引信噪声问题,采用全调节RBF神经网络构建非线性滤波器,自适应抵消回波信号中包含的干扰噪声。通过仿真对比,说明了该方法对引信回波噪声消除有较好的效果。
1 自适应干扰噪声的基本原理
自适应干扰对消器原理,如图1所示。
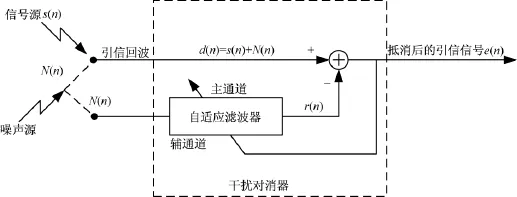
图1 自适应干扰对消器原理框图
图1中包括两个通道:主通道和辅通道。主通道要接收从信号源发来的信号s(n),但是受到干扰源的干扰。这时的主通道不仅收到信号s(n),也收到干扰N(n);辅通道的作用就在于检测干扰,并通过自适应滤波调整其输出r(n),使r(n)在某种算法下最接近主通道干扰N(n),即将噪声干扰N(n)对消掉。
辅通道收到的信号为干扰N(n),先假设信号源与噪声源相互无关,即s(n)和N(n)无关。在图1中,主通道的输入信号s(n)+N(n)成为自适应滤波器的需要信号d(n)。系统输出则取自误差信号:
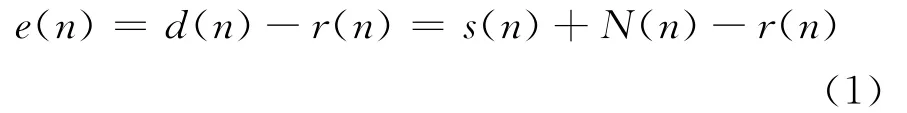
均方误差亦即输出的均方值

因为s(n)和 N(n)、r(n)无关,则E{s(N-r)}=0。
式(2)变为

自适应滤波器要调整其加权矢量,使E {e2}最小。因信号源s(n)不在自适应滤波器通道内,所以这种最小化可表示为
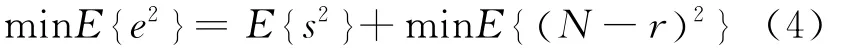
自适应调整的结果,使r(n)在均方误差最小的意义下,最接近主通道噪声分量N(n),因而使系统输出中的噪声大大降低。由式(1)可得
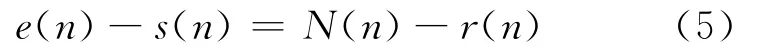
所以
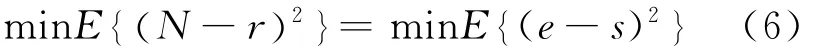
式(6)说明,在最小均方误差意义下,r(n)最接近N(n)等效于系统输出e(n)最接近s(n)。所以,在噪声对消器的输出端大大地提高了信号噪声比。
2 基于全调节RBF神经网络自适应噪声对消方法
首先介绍自适应滤波器中用到的全调节RBF神经网络。RBF神经网络是一种比较典型的局部逼近网络。本文中新颖的方面,就是采用与一般设计不同的全调节RBF神经网络,处理了非线性参数的不确定性,提高了神经网络的在线逼近能力[5]。所谓全调节RBF神经网络就是不仅调节RBF神经网络的权值,并且同时调节中心点值和影响范围,这样全调节RBF神经网络具有比一般RBF神经网络更强的在线逼近能力,其结构图如图2所示。
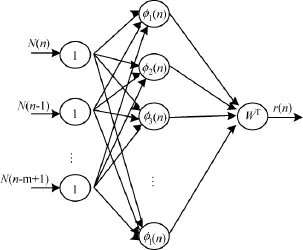
图2 全调节RBF神经网络结构图
根据图2可知
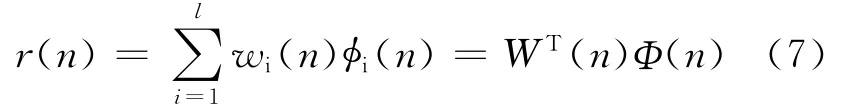
其中:
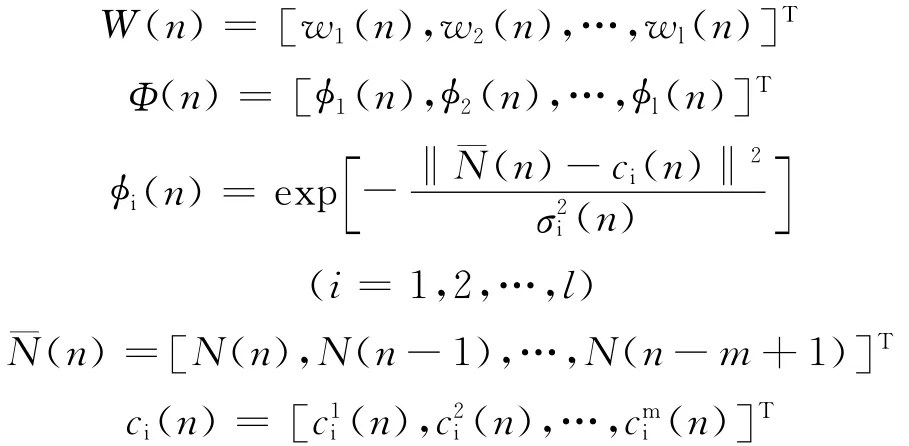
定义信号e(n)=d(n)-r(n)=d(n)-WT(n)Φ(n),性能函数ξ(n)=e2(n)。根据梯度下降法,神经网络的权值wi(n)、中心值ci(n)和影响范围σi(n)的变化律分别如下:

式中:φ′i(n)表示φi(n)的导数,μw、μc和μσ为设计参数。
3 仿真分析
引信回波信号检测的目的是消除背景噪声的影响,尽可能地获取目标的真实回波信号。为了评价本文方法的设计效果,将与文献[1]的方法进行对比分析。一般情况下,假设引信干扰为高斯白噪声信号,对一段标注引信发射信号和高斯白噪声进行仿真。
假设为连续波多普勒引信,生成的引信发射信号如图3所示。运用Matlab函数生成均匀分布的高斯白噪声,其信噪比为16 dB,与引信回波信号合成后的信号形式如图4所示。根据图1所示的噪声自适应对消系统和本文提出的基于全调节RBF神经网络滤波器,选取合理的设计参数,对图4的引信回波信号进行去噪,得到的仿真结果如图5所示。运用文献[1]的方法得到的仿真结果如图6所示。对比图5和图6的结果可知,运用本文方法获得的引信回波去噪后信号明显优于文献[1]的结果。
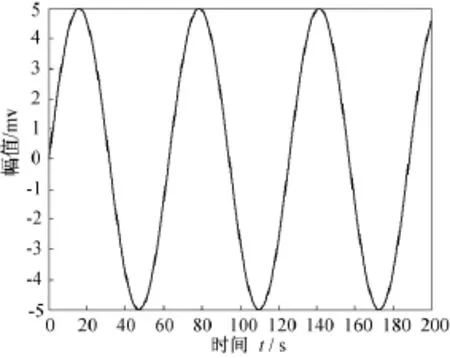
图3 引信发射信号
为了更好地说明基于全调节RBF神经网络滤波方法的效果,同时还采用了不同信噪比的噪声。当信噪比分别为12 d B和10 d B时,运用本文方法得到的去噪后波形分别如图7和图8所示。
对比图5、图7和图8可知,信噪比越高,系统的滤波效果越好。此外,全调节RBF神经网络参数的学习因子μw、μc、和μσ越大,信号的收敛速度越快,但是太大的学习因子取值,也会导致系统的不稳定。
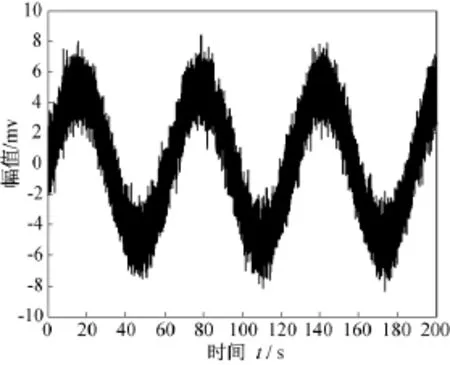
图4 带有噪声的引信回波信号
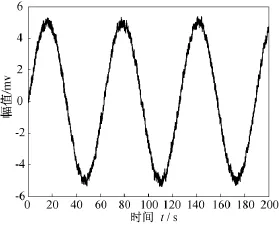
图5 运用本文方法的去噪后仿真结果
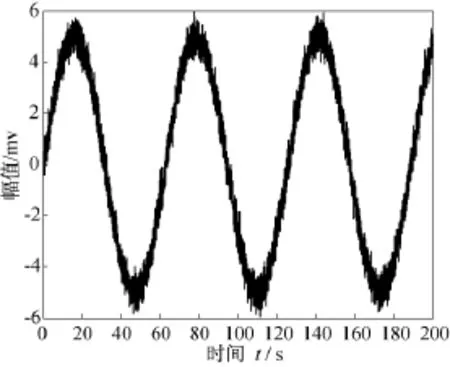
图6 自适应消噪方法去噪后仿真结果
4 结论
为了尽可能地消除引信回波中的噪声信号,本文提出了一种全调节RBF神经网络滤波器,并利用该滤波器设计出噪声自适应对消系统。通过对比不同信噪比情况下引信回波的去噪效果,说明了本文方法的有效性和优越性,并为引信噪声
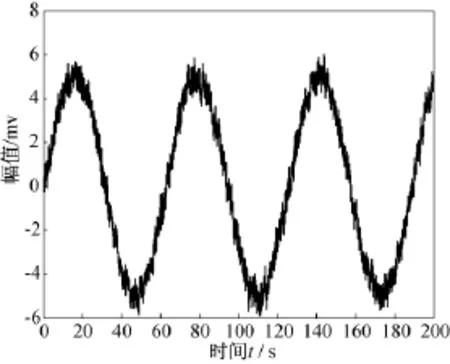
图7 信噪比为12 dB时本文方法得到的去噪后仿真结果
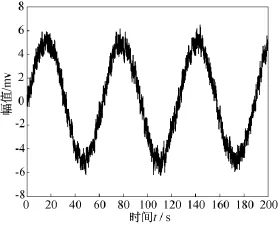
图8 信噪比为10 dB时本文方法得到的去噪后仿真结果
自适应对消系统的工程应用提供了很好的原理设计。
[1] 胡江波,王文刚,楼旭俊.BP网络自适应消噪方法在无线电引信中的应用[J].探测与控制学报,2008,30(5):45-47.
[2] 尹熙鹏,樊养余,段哲民,程伟.基于自适应小波神经网络实现鱼雷超声引信信号消噪[J].鱼雷技术,2009,17(5):19-22.
[3] 蒋静群,简金蕾,任宏滨.基于自适应神经网络滤波的引信去噪声研究[J].现代防御技术,2008,36(6):76-80.
[4] 简金蕾,乔健,任宏滨.基于神经网络的引信干扰信号对消[J].探测与控制学报,2005,27(3):23-25.
[5] 李静,左斌,胡云安.基于全调节RBF神经网络的远程网络控制器设计[J].控制与决策,2009,24(3):408-412.
