一种精简化的球杆系统控制器建模方法
2012-12-01钟秉翔高国芳
钟秉翔 高国芳
(重庆科技学院电气与信息工程学院,重庆 401331)
0 引言
在实际生活或工程实践中,一个熟练的操作人员凭借丰富的生活经验或实践经验,可以非常娴熟、巧妙地控制一个复杂过程,并得到满意的控制效果。能否采用自动控制的机器来代替人的行为,以及如何通过功能模拟实现这些有效的控制行为等关于人的控制行为功能模拟的智能控制器设计问题,均属于智能系统辨识或建模问题。众所周知,实现专家控制系统的前提是必须要有有效的专家经验知识;而模糊控制的设计必须依据人类直接控制被控对象的成功经验,没有这类经验,模糊规则将无法设计。
理论研究表明,基于神经网络、自适应模糊系统的控制系统具有一定的学习能力,能够更好地适应环境和系统特性的变化,适合不确定复杂系统的建模与控制。然而,随着问题复杂性的增加,计算机控制系统在执行数值运算时需要的时间呈指数增长,计算量呈指数增长,易出现维度灾难[1-3]。分析国内外关于模糊系统、神经控制器和支持向量机模型精简化研究的现状发现,这些系统都局限于模型内部结构的优化[4-6]。
本文针对控制器变量众多、易出现维度灾难、系统复杂性增加等问题,以球杆系统作为研究对象,设计了精简化的球杆系统控制器模型。通过寻找输入空间的主要特征变量,剔除次要因素,精简输入空间维数,减少控制系统数学模型复杂性;同时采用核函数方法和虚假最近邻点法,实施智能控制器模型的非线性回归建模,实现球杆系统的自动控制。
1 理论基础
本文从输入空间维数的精简和优化角度考虑,运用虚假最近邻点法(faulse nearest neighbor point algorithm,FNN)确定输入向量嵌入维数,再通过核主元分析法(kernel principal component analysis,KPCA)提取特征值,实现了对非线性辅助变量空间的特征提取。
1.1 虚假邻点法
虚假邻点法的基本思想是当维数从m变成(m+1)时,考察轨线x的邻点中的真实邻点和虚假邻点[7]。当没有虚假的邻点时,可以认为吸引子的几何结构被完全展开。设xβ(n)为xn的最近邻点,它们之间的距离为‖xβ(n)-xn‖(m),当维数增加到 m+1时,它们之间的距离为‖xβ(n)- xn‖(m+1)。若‖xβ(n)- xn‖(m+1)比‖xβ(n)-xn‖(m)大很多,可以认为这样的邻点是虚假的。因此,若式(1)成立,则称xβ(n)为xn的虚假邻点,其中,Rt为阈值。
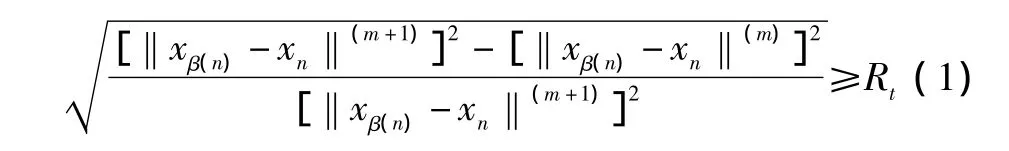
试验证明,Rt可在[10,50]之间选取。对于无限长的精确数据,采用上述标准可获得较好的结果。对于有限长具有噪声的数据,则补充以下标准,若:
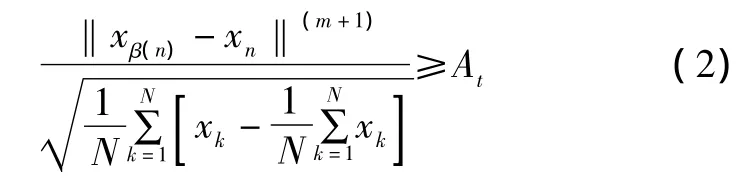
则称 xβ(n)为xn的虚假邻点,At为阈值。文献[8]建议取At=2。
对实测时间序列,m从2开始,计算虚假最近邻点的比例,直到虚假最近邻点的比例小于5%。当虚假最近邻点不再随着m的增加而减少时,可认为吸引子的几何结构完全打开,此时的m即为嵌入维数。
1.2 核函数主元分析的基本原理
核主成分分析(KPCA)法利用核映射的原理,将原始空间的数据映射到高维特征空间,在特征空间中再对数据进行线性主元分析(principal component analysis,PCA)分析(对应于原始空间的非线性运算)[8-11]。因此,它实现了样本空间的非线性特征提取,具体的算法实现过程如下。
设X为原始空间Rn×l中的样本数据,n为变量维数,l为样本数。对其进行非线性变换Φ(X)后,将其映射到高维特征空间H中。Φ(X)的协方差矩阵C的表达式为:
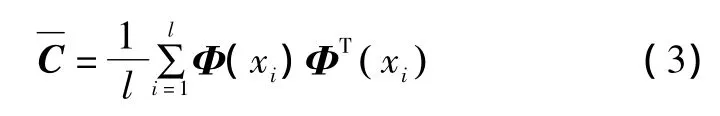
特征向量v为原始样本空间x在特征空间Φ(X)上的主元方向,其满足:

将每个样本 xj(j=1,2,…,l)变换为 Φ(xj)后,与式(4)进行内积运算,可得:
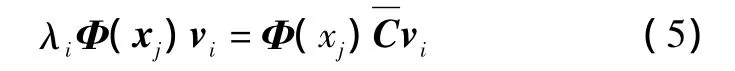
由于vi是Φ(xi)的线性组合,于是存在αi(i=1,2,…,l)满足:
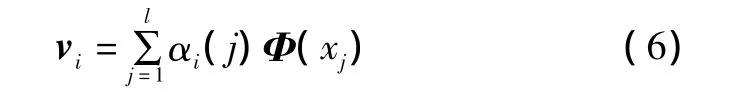
式中:j=1,2,…,l;αi(j)为向量 αi的第 j个元素。
将式(3)、式(6)代入式(5),可得:
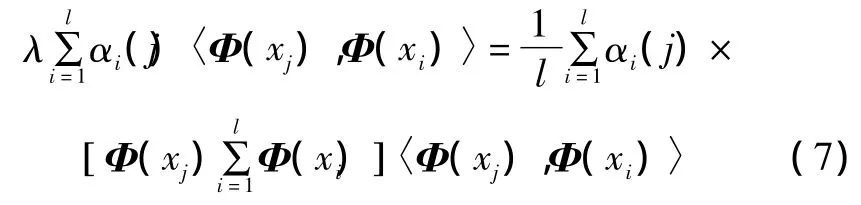
式中:i=1,2,…,l;特征值 λi≥0。
在再生核希尔伯特空间(reproducing kernel Hilbert space,RKHS)中,满足Mercer定理的核函数对应非线性函数的内积运算,即:
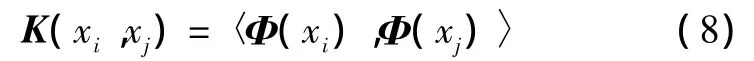
这里,核矩阵要经过中心化处理。利用式(8),可将式(7)变为:

式中:α 为特征向量,且 α=[α1,…,αl]。
在特征空间中,特征向量 α=[α1,…,αl]经过PCA特征提取后,将得到满足主元贡献率的前k个主元向量α=[α1,…,αk]以及相应的主元特征向量v=[v1,…,vk]。在此基础上,原始空间X的主元向量=(x1,x2,…,xk)可通过Φ(X)在主元方向v上的投影得到,即:

式中:p=1,2,…,k;αp(i)为特征向量 αp中的第 i个元素;vp为v的第p个特征向量;K( xi,x)为核函数。
通过以上步骤,不但实现了矩阵从X∈Rl×n到~X∈Rl×k的非线性特征提取,同时也实现了非线性辅助变量空间的特征提取。
2 球杆系统结构
为模拟人工操纵小球在横杆的某一指定位置,采用固高科技有限公司的球杆系统GBB1004,通过自动控制电机的转动,使小球稳定在横杆上的某一平衡位置。球杆系统主要由机械部分和智能伺服驱动和控制计算机等部分组成。其中机械部分包括底座、小球、横杆、减速皮带轮、支撑部分、马达等,球杆系统机械部分结构如图1所示。
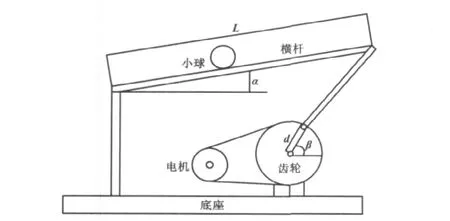
图1 球杆系统机械部分结构Fig.1 Partial structure of the mechanical part of the cue system
小球可以在横杆上自由滚动,横杆的一端通过转轴固定,另一端由一连杆与齿轮相连,可以上下转动。通过控制直流伺服电机的位置,带动皮带轮转动,再通过传动机构就可以控制横杆的倾斜角α。直流伺服电机带有增量式编码器,可以检测电机的实际位置β。在横杆上的凹槽内,有一线性的传感器用于检测小球的实际位置。α和β两个实际位置的信号都被传送给控制系统,构成一个闭环反馈系统。当皮带轮转动角度为β、横杆的转动角度为α、连杆和齿轮的连接点与齿轮中心的距离为d、横杆的长度为L时,横杆的倾斜角α和β之间存在以下数学关系:

电机的运动通过IPM100智能伺服驱动器进行控制,IPM100是一个智能的高精度、全数字的控制器,内嵌100 W的驱动电路。基于反馈控制原理,在得到传感器信号后对信号进行处理,然后给电机绕组施加适当的PWM电压信号,这样,相应的转矩作用于电机轴,使电机开始运动。
3 球杆系统控制方案
球杆系统是一个典型的非线性系统,球杆系统中小球位置的控制不仅与横杆的实际位置和小球的实际位置有关,还与以前的横杆和小球的位置有关。因此,小球位置可以表示为关于小球的时间序列和横杆位置的时间序列非线性方程。小球系统的非线性方程可以表示为:

式中:x1(k),x1(k-1),…,x1(k-m1),x2(k),x2(k-1),…,x2(k- m2)为原始变量组;x1(k),x1(k-1),…,x1(k-m1)为小球位置的时间序列;x2(k),x2(k-1)…,x2(k-m2)为横杆转角的时间序列;m1、m2分别为时间序列的嵌入维数。
在处理非线性输入变量选择问题时,可合理地提取特征和减少维度。为此,建立的球杆系统控制器数学模型如图2所示。

图2 球杆系统控制器数学模型Fig.2 The mathematical model of the cue system controller
由于模型的阶数和信息融合结构均未知,如考虑所有的输入时延信息,将大大降低其实时性能。因此,可采用本文的方法进行输入相空间的特征提取和信息融合相空间结构的确定。
由于球杆系统控制器的输入相空间由小球位置信号和横杆转动角度及其时间延时组成,而球杆系统是一个模型阶数、结构均未知的复杂系统。因此,首先要选择小球位置信号和横杆转动角度及其时间序列,通过虚假邻点法计算输入样本的嵌入维数,从而确定作为球杆控制器模型的初始输入相空间。
建立球杆系统所需的原始样本数据经过采集卡采集至计算机,共采集500组数据。本文通过异常点剔除和归一化处理后,把剩下的488个数据分成两组,其中400个数据用来建模和交叉检验,另外88个作为测试数据集。
4 试验结果
样本数据经标准化后,利用虚假邻点法计算输入样本的嵌入维数,所得虚假最近邻点比例与嵌入维数关系如表1所示。
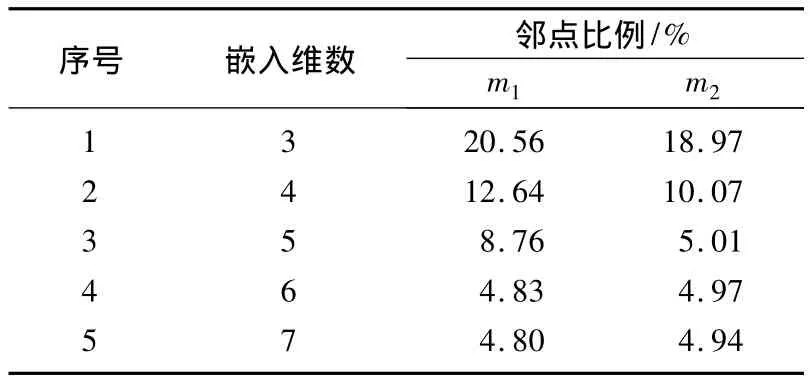
表1 邻点比例与嵌入维数关系Tab.1 Relationship between proportion of neighbor point and embedded dimensionality
从表1可以看出,m1增加到6,m2增加到5,虚假最近邻点不再减少,所以嵌入维数取m1为6,m2为5。
根据KPCA原理,可以计算出经KPCA提取出的主成分、与主成分对应的各方差贡献率以及总方差贡献率,主元分析结果如表2所示。
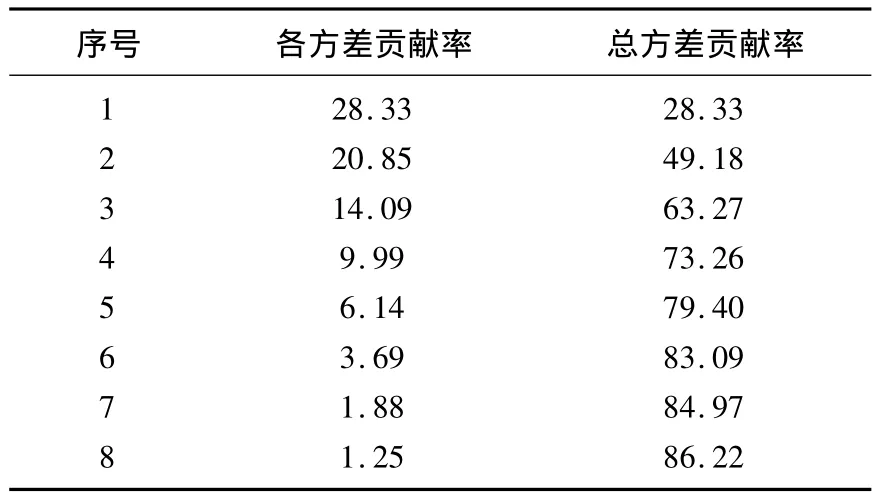
表2 主元分析结果Tab.2 Result of principal component analysis%
表2中,前8个主元的总累计方差贡献率已经达到了86.22%。文献[10]提出当前k个主元所累积的方差贡献率足够大时(一般大于85%),就可以只取前k个主元作为新特征向量,即可以很好地反映过程信息而滤去冗余信息。因此,可认为前8个主成分已无相关性,且包括了原始数据的绝大部分信息,则选择上述8个主元分量建立模型,利用最小二乘法即可建立数学模型。
不同模式下的控制效果比较曲线如图3所示。
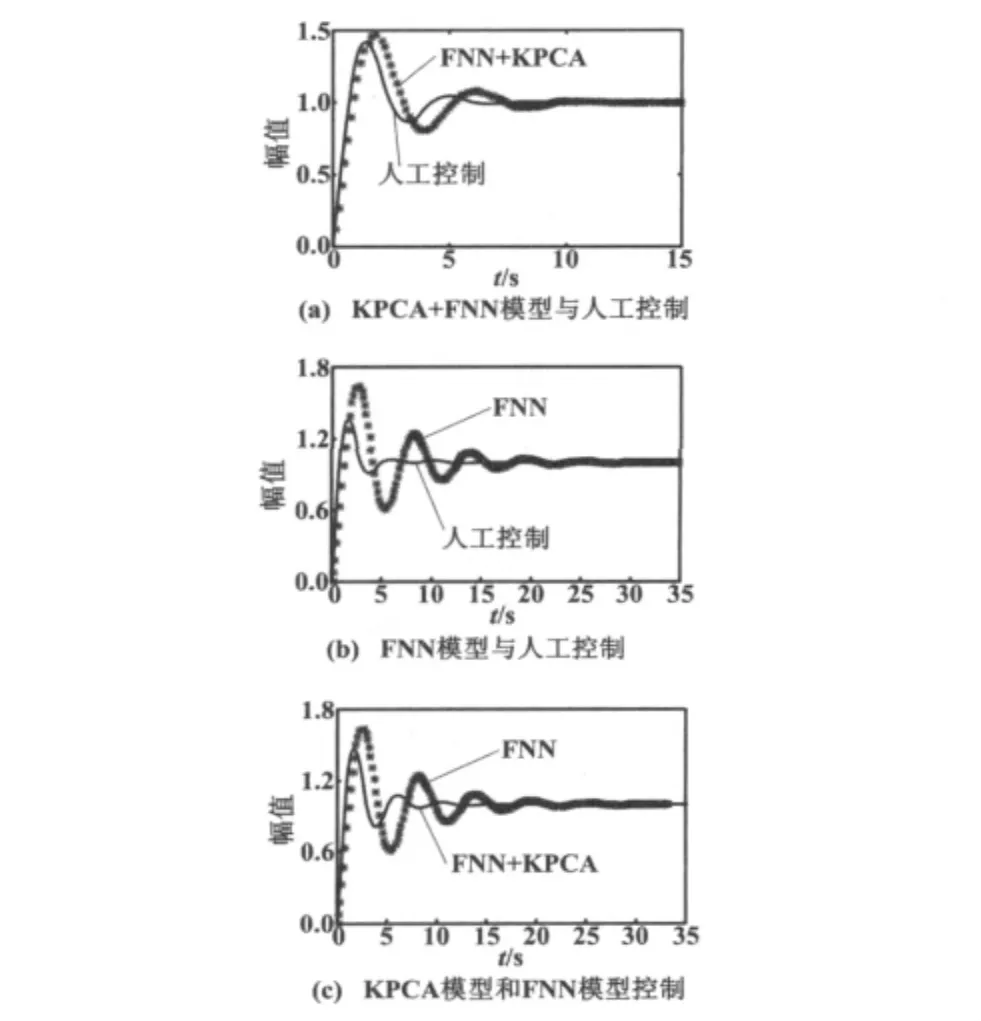
图3 控制效果比较曲线Fig.3 Comparison curves of control effects
模型的训练精度和泛化能力可以用均方根误差(root mean square percentage error,RMSPE)表示,其可定义为:
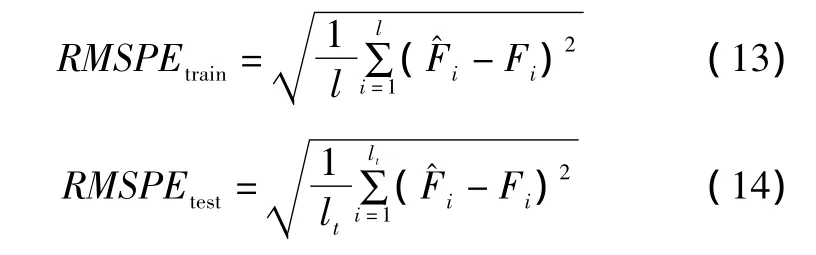
根据样本数据和测试数据,计算其训练误差和测试误差,计算结果如表3所示。

表3 两种建模方法的精度比较Tab.3 Precision comparison of two modeling methods
从仿真试验结果可知,2种模型都能达到预期效果;但从模型检验来看,KPCA+FNN模型具有较好的泛化能力。综合考虑模型的复杂性、控制精度和泛化能力,KPCA+NN的建模方法更适合用于功能模拟智能控制器模型设计。
5 结束语
本文设计的球杆系统控制器利用虚假最近邻点法确定球杆系统的输入向量维数[12];采用核主元分析方法提取输入特征向量,精简输入空间的维数;利用最小二乘法进行线性回归,建立球杆控制系统的数学模型。试验结果表明,基于虚假最近邻点法和核主元分析法的球杆系统控制器能较好地模拟人的控制行为且有较好的泛化性能。该建模方法有利于提高球杆控制系统的稳定性和控制精度,减少输入变量嵌入维数,避免维度灾难,从而为解决复杂控制系统中易出现的的维度灾难和精简化建模等问题提供了一定思路。
[1]Bengio S,Bengi Y.Taking on the curse of dimensionality in joint distributions using neural networks[J].IEEE Transactions on Neural Networks,2000,11(3):550 -557.
[2]Paul M.Class-specific classifier:avoiding the curse of dimensionality[J].IEEE A & E Systems Magazine,2004,19(1):37 -52.
[3]Guven M K,Passino K V.Avoiding exponential parameter growth in fuzzy systems[J].IEEE Transactions on Fuzzy Systems,2004,19(1):194 -199.
[4]Li T F,Su Y Y,Zhong B X.Remodeling for fuzzy PID controller based on neural networks[C]//2007 Advance in Soft Computing,Springer-Verlag,2007:714 -725.
[5]Li C S,Lee C Y.Self-organizing neuro-fuzzy system for control of unknown plants[J].IEEE Transactions on Fuzzy Systems,2003,11(1):135-150.
[6]陈永义,俞小鼎,高学浩,等.处理非线性分类和回归问题的一种新方法(I)——支持向量机方法简介[J].应用气象学报,2004,15(3):345 -354.
[7]王海燕,卢山.非线性时间序列分析和应用[M].北京:科学出版社,2006.
[8]Kennel M B,Brown R,Abarbanel H D.Determining embedding dimension for phase space reconstruction using a geometrical construction[J].Phisical Review,1992,45(6):3403 -3411.
[9]Sun Z L,Huang D S,Cheung Y M.Extracting nonlinear features for multispectral images by FCMC and KPCA[J].Digital Signal Processing,2005,15(4):331 -344.
[10]Lee J M,Chang K Y,Sang W C.Nonlinear process monitoring using kernel function principalcomponentanalysis[J].Chemical Engineering Science,2004,59(1):223 -234.
[11]王华忠,俞金寿.核函数方法及其在过程控制中的应用[J].石油化工自动化,2005(1):25-30.
[12]王秋红.ITCC压缩机控制系统在乙烯装置中的应用[J].石油化工自动化,2006,39(3):39 -41.
