多轴数控机床转台几何误差辨识新方法

冯 刚，付国强，孙 磊，傅建中

（1.浙江工业职业技术学院 浙江 绍兴312000；2.浙江大学 机械工程学院 浙江 杭州310027）

随着制造业的快速发展，五轴数控机床的作用越来越明显.五轴数控机床的2个旋转轴可以提高机床切削率，降低切削时间，减少工件装夹次数［1］.机床精度是机床重要参数之一，直接影响加工工件质量.影响机床精度的因素有多种，其中几何误差和热误差占60%左右［2］.机床几何误差建模与补偿成为提高机床精度的重要途径之一.

机床几何误差模型是误差补偿的基础，多体理论是进行误差建模的依据［3-5］.指数积理论可建立机床的几何误差模型［6］，直角坐标系之间的微分变换关系也是进行建模的手段之一［7］.几何误差项的辨识是误差建模的基础.旋转轴几何误差项的辨识是五轴数控机床建模与补偿的关键步骤之一，国内外学者提出了很多辨识方法［8-10］.Tsutsu等［11］采用三轴同步运动的方法保持球杆仪方向相对于测量旋转轴坐标系不变来辨识旋转轴特有的位置和角度偏差.Zargarbashi等［12］采用A 轴单独运动形式设计5个球杆仪测量路径根据得到的球杆仪读数模型来辨识得到A 轴的5项几何误差.Lee等［13］根据几何误差项性质采用参数化形式表示旋转轴误差项，提出5种测量模式来辨识相应参数.Lee等［14-15］针对每个旋转轴设计2种测量路径用球杆仪辨识垂直度误差和位置偏差，并考虑球杆仪安装误差的影响.Zhang等［16］用球杆仪和高度调节装置设计出不同水平面上的2条测量路径来辨识C 轴的五项几何误差.但是得到的五项几何误差为恒定值，与误差性质不符.Chen等［17］构建矩阵形式的辨识模型，并在3个不同测量点的球杆仪读数来辨识6 项几何误差，并通过4个特殊路径得到球杆仪在转台上的安装误差.

每个旋转轴应包含6项基本几何误差、2 项垂直度误差和2项位置误差.这些辨识方法可以得到旋转轴部分几何误差项，为进一步研究提供了依据.然而没有一种方法可得到旋转轴的全部几何误差项.大部分方法采用三轴同步运动来运行测量路径，测量过程中会引入线性轴的误差，影响辨识精度，且同步运动轴的不同步误差也会影响精度.

针对这些问题，本文针对转台（C 轴）几何误差项提出了一种系统性辨识方法.该方法只需C 轴单独旋转，能够得到C 轴的10项几何误差.首先结合球杆仪方向向量得到C 轴几何误差项与球杆仪读数关系.其次提出基于球杆仪的六步骤测量法，来辨识10项几何误差.分析了球杆仪安装误差对辨识精度的影响并采用数据拟合的方法消除其影响.接着仿真验证了六步骤测量法的正确性.最后通过实验验证该方法的有效性和正确性.

1 转台测量的球杆仪读数模型

在球杆仪测量时一端安装在主轴刀柄上，称为刀具球，另一端固定在转台上称为工件球.转台旋转时，其几何误差会使得球杆仪长度发生变化.根据转台误差齐次矩阵和球杆仪初始位置可以得到球杆仪刀具球和工件球在转台坐标系下的坐标，从而得到球杆仪读数与转台几何误差之间的关系.

转台（C 轴）的6项基本几何误差包含3项线性误差和3项转角误差，如图1 所示.δxc、δyc、δzc分别表示x、y、z方向的线性误差，εxc、εyc和εzc分别表示绕x、y、z轴的转角误差.C 轴2项垂直度误差分别为C 轴和X 轴之间的Scx和C 轴和Y 轴之间的Scy，2项位置偏差分别为x 方向的ocx和y 方向的ocy.那么转台的误差齐次矩阵可表示为［18］

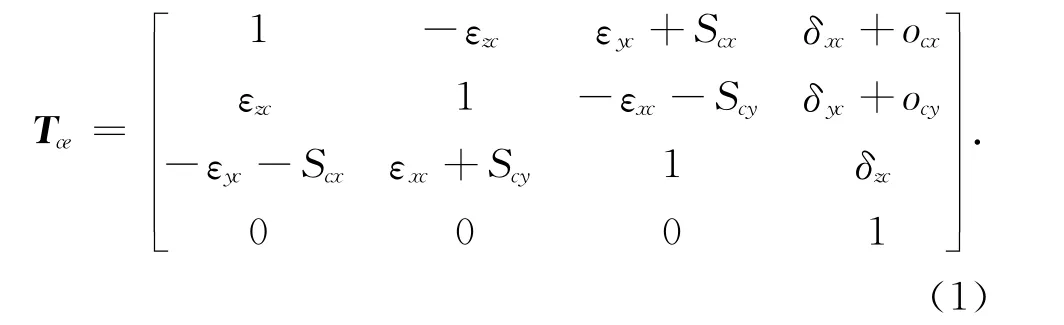
式（1）表示垂直度误差可视为为恒定值转角误差，位置偏差可作为线性误差一部分，那么根据该性质，为了方便可先不考虑垂直度误差和位置误差的影响.C 轴理想齐次转换矩阵可表示为

当转台单独旋转时，平动轴和其他旋转轴都是保持静止的，那么它们几何误差项对球杆仪读数没有影响，即平动轴和其他旋转轴的几何误差在这里忽略不计，球杆仪刀具球在转台坐标系下的齐次坐标可表示为

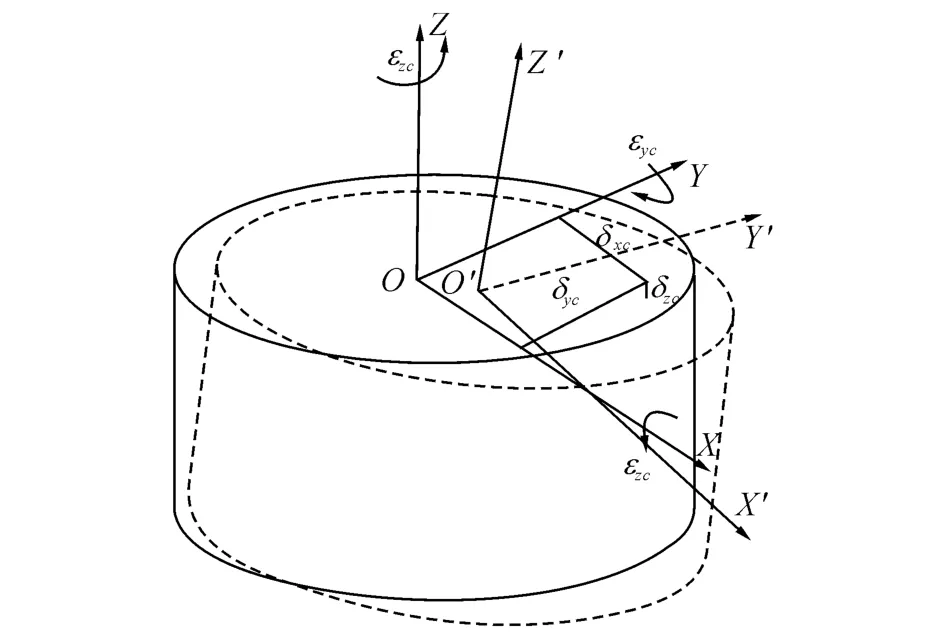
图1 转台6项基本几何误差示意图Fig.1 Six basic geometric error components of turntable

式中：x、y、z表示刀具球在机床参考系下的初始坐标值.

工件球固定在转台上，随转台一起运动，工件球的齐次坐标是保持不变的，可表示为

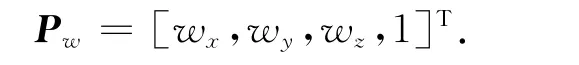
球杆仪读数与2个球坐标之间的关系可通过球杆仪方向向量建立起来，球杆仪方向向量表示在转台坐标系下，工件球指向刀具球的单位向量，代表了球杆仪可以测量该方向上的综合误差.那么球杆仪读数可表示为

式中：R 为球杆仪公称长度，ΔR 为球杆仪长度变化量，V ＝［vx，vy，vz，0］T，vx、vy、vz分别为球杆仪方向向量在x、y 和z 方向上的分量.那么球杆仪读数模型可通过式（3）表示为

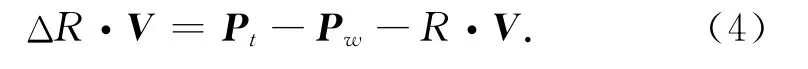
因为球杆仪方向向量为单位向量，式（4）又可以表示为

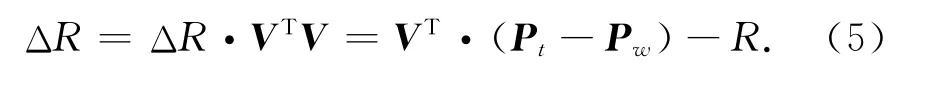
2 转台几何误差辨识

用球杆仪测量旋转轴几何误差时，球杆仪路径是圆或者圆弧.对于转台来说，它的旋转轴线可根据机床结构轻易定位得到，这样转台的单独旋转就可以完成球杆仪的测量辨识.根据转台单独运动时球杆仪读数与转台几何误差的关系，提出了六步骤测量法.如图2所示表示了六步骤测量法中每个步骤球杆仪的安装位置.这些球杆仪的安装时很简单的，其位置也没有特殊要求，可以很容易的定位得到，这样就大大的提高了测量的效率.按照六步骤测量法得到各个步骤中相应的球杆仪读数，可辨识得到转台的几何误差项.这六步骤可辨识得到转台所有的10项几何误差项.

2.1 六步骤测量法

根据每个步骤中球杆仪的方向向量和位置，结合球杆仪读数与几何误差之间的关系可得到相应几何误差项的辨识公式.为了方便，根据式（1）可先不考虑垂直度误差和位置误差的影响.下面对每个步骤进行分析以得到几何误差辨识公式.

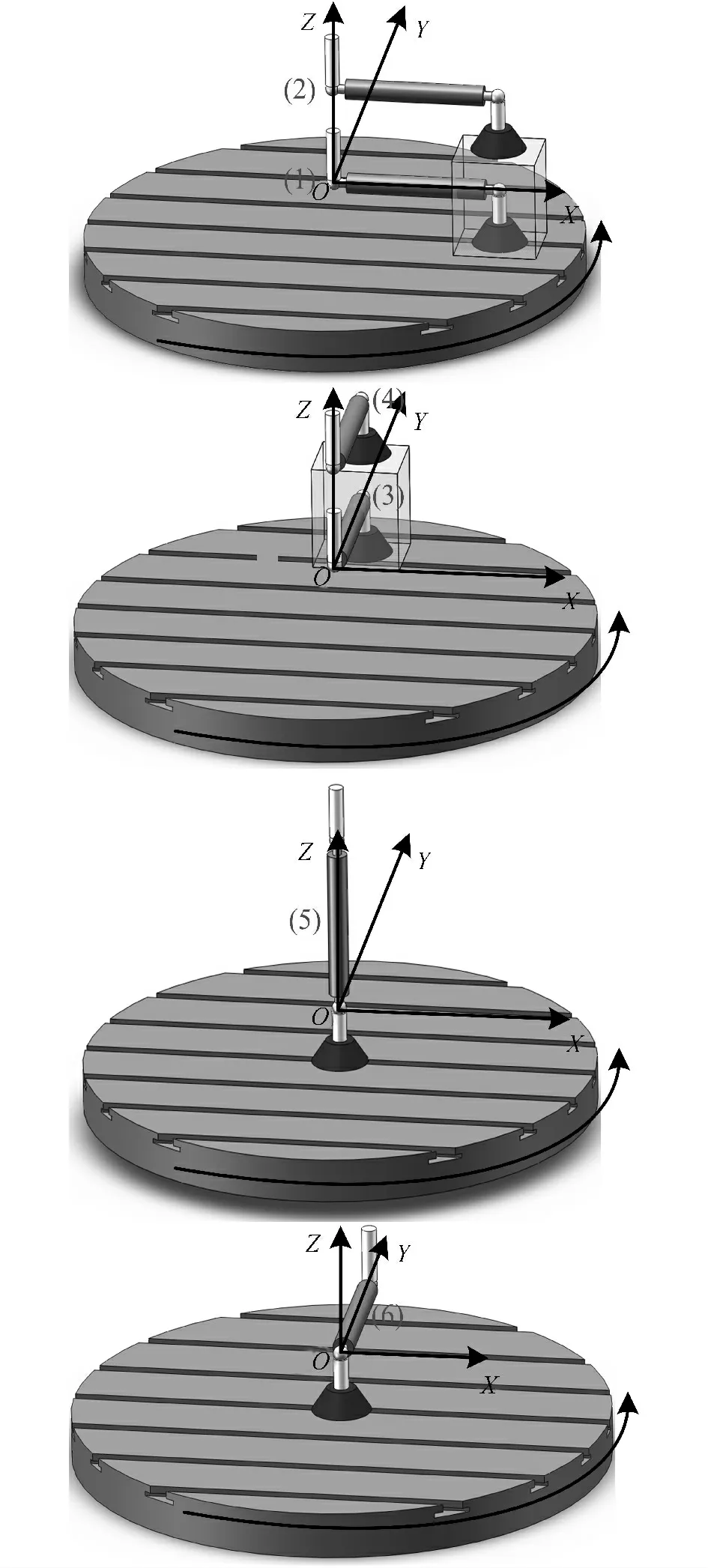
图2 六步骤测量法中球杆仪的安装位置Fig.2 Installation of ballbar in six-step measurement

如图2所示，步骤1和2的球杆仪刀具球初始位置在转台旋转轴线上，且球杆仪均位于转台坐标系的x 轴方向，但是刀具球z向高度有所区别.那么刀具球的初始位置坐标可表示为［0，0，z］.那么根据式（2）可得到球杆仪刀具球相对于转台的齐次坐标为

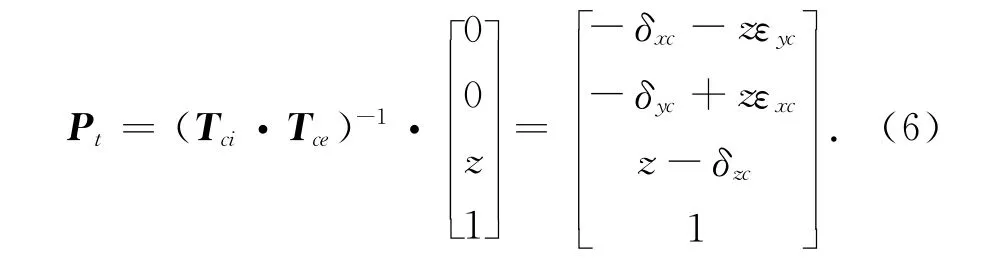
球杆仪工件球与刀具球在同一水平面上，当转台单独旋转时球杆仪随转台同步运动与转台保持相对静止，那么球杆仪在转台坐标下的方向向量保持不变，表示为V1，2＝［-1，0，0，0］T，工件球的坐标为［R，0，z］.那么根据式（5）可以得到步骤1和2中球杆仪读数与相应几何误差关系为

即

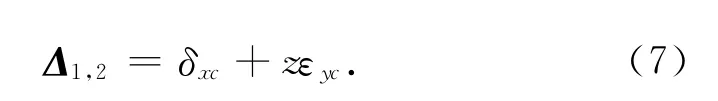
式中：Δ1，2为步骤1和步骤2球杆仪读数.为了方便辨识，步骤1中刀具球初始z 坐标为0，步骤2中z坐标为L，如图2所示，根据式（7）可以得到相应线性和转角几何误差辨识公式为

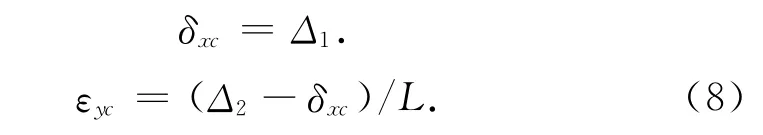
式中：Δ1为步骤1中球杆仪读数，Δ2为步骤2中球杆仪读数，

对于步骤3和4，刀具球坐标分别于步骤1和2中是一样，即步骤3中刀具球初始z坐标为0，步骤4中z坐标为L，那么式（6）也表示了这2个步骤中球杆仪刀具球在转台坐标下的坐标.不同之处为球杆仪的方向向量与转台y 轴方向平行，即V1，2＝［0，-1，0，0］T，工件球坐标为［0，R，0］，那么同样的根据式（5）可以得到球杆仪读数与相应几何误差关系为

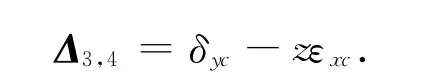
式中：Δ3，4为步骤3和步骤4球杆仪读数，那么相应的几何误差辨识公式可由球杆仪读数表示为

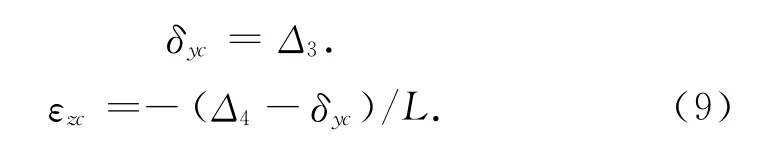
在步骤5中，刀具球和工件球都位于转台旋转轴线上，刀具球初始z坐标为R，工件球z坐标为0，球杆仪方向向量为V1，2＝［0，0，1，0］T，那么同样的根据式（5）和（6）得到

步骤6的工件球在转台旋转轴线上，其坐标为［0，0，0］，而刀具球的初始位置坐标为［0，R，0］.当转台单独旋转时，球杆仪相对于转台的方向向量是随着转台转角发生变化的.如图3所示表示了球杆仪方向与转台坐标系之间的关系.球杆仪与转台坐标系Y 轴之间的夹角为转台转角γ，那么球杆仪方向向量可表示为V6＝［sinγ，cosγ，0，0］T，根据式（2）得到刀具球在转台工件坐标系下的坐标为

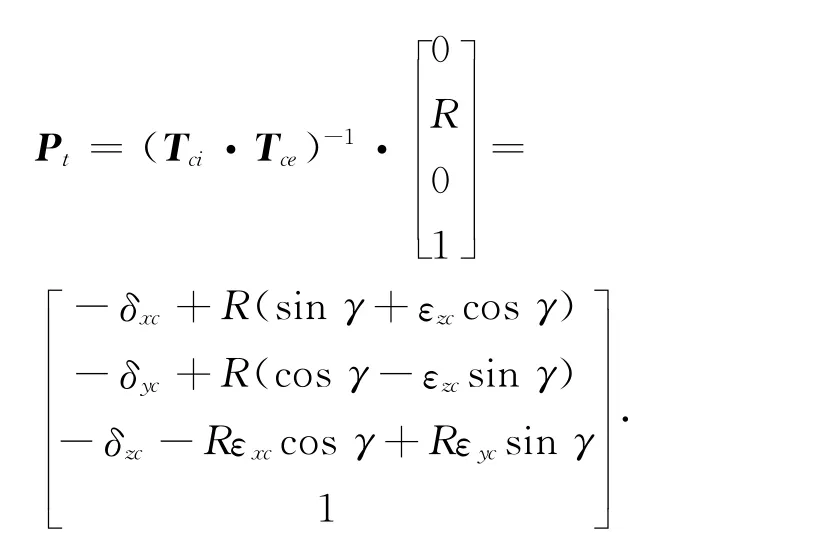
式中：γ表示转台的转角，即转台的位置.那么球杆仪读数和几何误差之间的关系可根据式（4）表示为

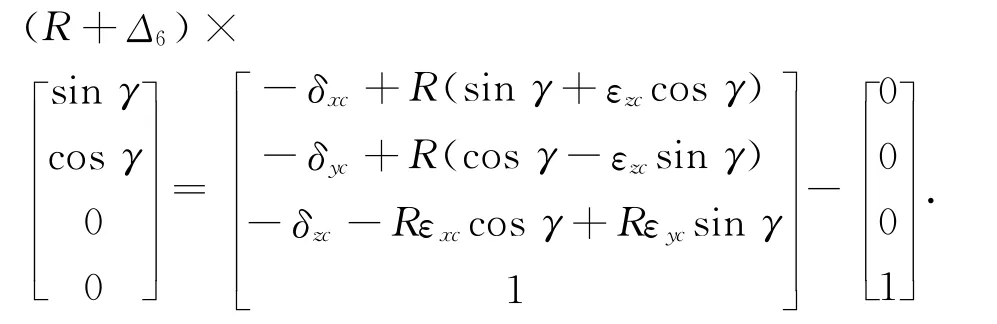
整理可以得到

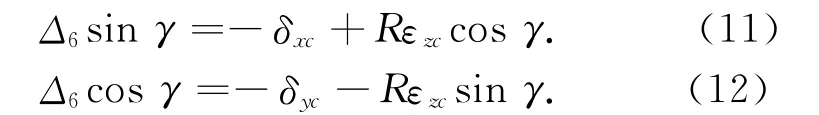
式（11）、（12）中的δxc和δyc已经辨识得到，只需对εzc进行辨识即可.根据式（11）辨识时，在γ＝0°，180°，360°这几个特殊位置处，球杆仪读数在该式子中反映不出εzc误差项，而在90°和270°处εzc对球杆仪读数无影响.同样的，用式（12）辨识时，在这几个特殊位置处，球杆仪读数无法反映该误差项，或者该误差项对球杆仪读数无影响.为了能够充分使用球杆仪读数，同时式（11）和（11）辨识误差，除了这几个特殊位置外，几何误差项可表示为

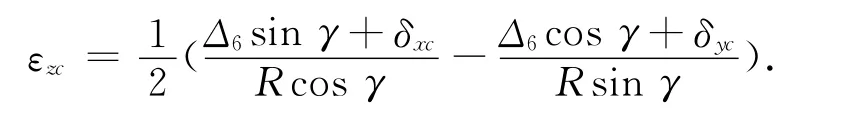
当γ＝0°和360°时，转台基本误差项数值应为零，而在γ＝90°，180，360处，εzc误差值可根据前后相邻位置点的误差值进行插值得到.因为在球杆仪测量时，数据记录间隔恒定的，那么在这3个角度处的误差数值可表示为

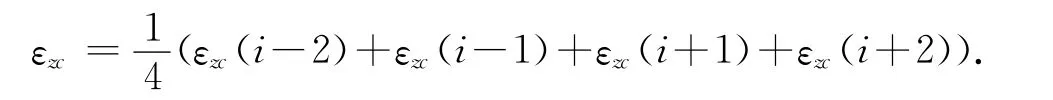
式中：i为数据采集时这3个角度相应的位置序号.那么εzc的辨识公式可表示为

那么式（8）、（9）、（10）和（13）为转台几何误差表达式.转台旋转一个角度，球杆仪就有个对应的读数，那么由这4个式子根据球杆仪读数得到的几何误差是相对于转台转角变化的值.

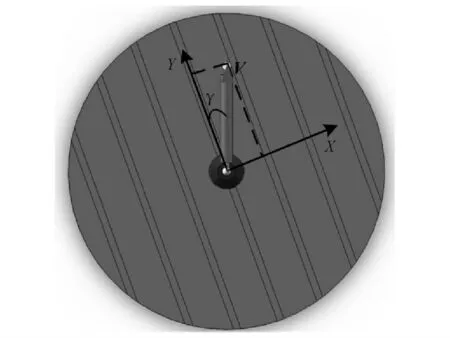
图3 球杆仪方向与转台坐标系之间的关系Fig.3 Relationship between direction of ballbar and coordinate system of turntable

2.2 垂直度误差和位置偏差辨识

前面没有考虑垂直度误差和位置误差的影响，采用的处理方法是根据式（1）将垂直度误差作为相应转角误差的一部分，位置偏差作为相应线性误差的一部分.那么就需要进一步对垂直度误差和位置误差进行辨识，同时进一步对六项基本误差项进行修正.

垂直度误差和位置误差是与位置无关的误差，即与转台旋转角度无关，是一个恒定值.六项基本误差项是随着运动轴的运动而变化的，另外在运动轴初始位置基本误差项数值为0.即根据式（8）、（9）、（10）和（13）得到的误差项是基本误差项加上相应的垂直度误差或者位置偏差的综合性误差.可以根据在转台零位置处的综合误差数值分离得到相应的垂直度误差和位置误差，同时对其他转角位置处的综合误差进行修正得到机床基本误差项数值.

式（1）中垂直度误差Sc为定值的y 方向的转角误差，Scy为x 方向的转角误差，位置误差ocx作为x方向的线性误差δxc，ocy是y 方向的线性误差δyc.在转台转角为零时，转角误差εyc和εxc为0，同时线性误差δxc和δyc为0.所以在零角度处由式（8）和（9）辨识得到的综合线性误差δxc为位置误差ocx，δyc为安装误差ocy，综合转角误差εyc为垂直度误差Scx，εxc为垂直度误差Scy，.在转台其他转角处分离出相应的垂直度误差和位置误差得到相应的基本误差项，同时对于z方向的转角误差和线性误差也需要进行同样的分离处理得到符合误差几何性质的基本误差数值.那么转台10项几何误差项表达式可表示为

式中：εkc′和δkc′表示由式（8）、（9）、（10）和（13）辨识得到的综合几何误差项.k＝x，y，z.

2.3 仿真分析

对六步骤测量法采用仿真分析来验证其正确性.首先产生转台的10项几何误差项数据，其中垂直度误差和位置误差为定值，6项基本几何误差项其随C 轴旋转角度的变化而变化，这里基本误差项数据以三次多项式的形式产生.根据基本误差项的性质，相应的三次多项式形式为

f（γ）＝aγ（γ-360）（γ-b）.不同的误差项选择不同的a 和b 值.产生的基本误差项数据见图5中仿真数据曲线所示，包括产生的线性误差和转角误差.垂直度误差和位置偏差数据设置见表1 中仿真值.仿真时球杆仪长度为100mm，步 骤2 中 球 杆 仪 工 件 球z 坐 标L ＝100 mm，同样的步骤4中工件球z坐标L＝100mm.然后根据球杆仪读数与几何误差之间的关系按照式（4）或者式（5）计算得到每个步骤中球杆仪读数，同时增加随机噪声得到相应的测量数据.如图4所示仿真得到的各个步骤中球杆仪数据.根据六步骤测量法，结合仿真产生的球杆仪数据结合式（8）、（9）、（10）、（12）和（13）辨识得到转台十项几何误差项.如表1所示为垂直度误差和位置误差的仿真结果.仿真产生和辨识得到的垂直度误差残差在1μm 以内，位置误差的残差更小.如图5所示为6项基本误差项的仿真值与计算值的比较结果.图5（a）为三项线性误差的仿真结果，图5（b）为三项转角误差的仿真结果.线性误差的计算值与仿真值非常接近，说明线性误差的辨识精度很高.而转角误差计算值与仿真值之间残差在噪声范围内.仿真结果表明了六步骤测量法是可行的.

表1 垂直度误差和位置偏差的仿真结果Tab.1 simulated results of squareness errors and offset errors

3 安装误差的影响

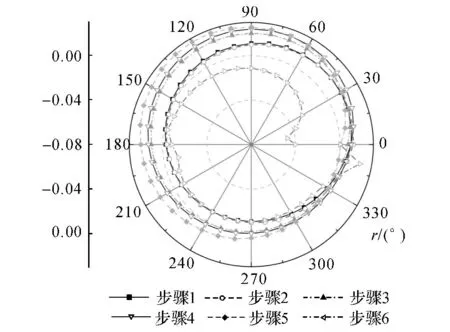
图4 各个步骤球杆仪仿真读数Fig.4 Simulated ballbar readings of each step

球杆仪在安装时不可避免的存在安装误差，安装误差对转台几何误差的辨识精度造成一定的影响.即使使用精密微调装置，球杆仪也同样的存在一定的安装误差，而球杆仪安装误差需要额外的工作量或者精密装置来测量得到［10，17］.另外同样的位置，安装一次球杆仪其安装误差就可能不同.而用六步骤测量时每个步骤都需要重新安装球杆仪，如果每安装一次球杆仪就用测量一次安装误差，这会大大增加测量的工作量.这里通过分析每个步骤中球杆仪安装误差对球杆仪读数的影响，然后采用最小二乘法根据其影响进行拟合，得到消除球杆仪安装误差后的读数，然后再进行几何误差的辨识，这样可以大大提高辨识精度，又不会增加测量的工作量.

球杆仪刀具球和工件球都存在安装误差，假设刀具球的安装误差为Δtx，Δty和Δtz，工件球的安装误差分别为Δwx，Δwy和Δwz.那么根据式（5）得到

那么根据式（15）结合各个步骤中球杆仪方向向量可以得到球杆仪安装误差对球杆仪读数的影响为

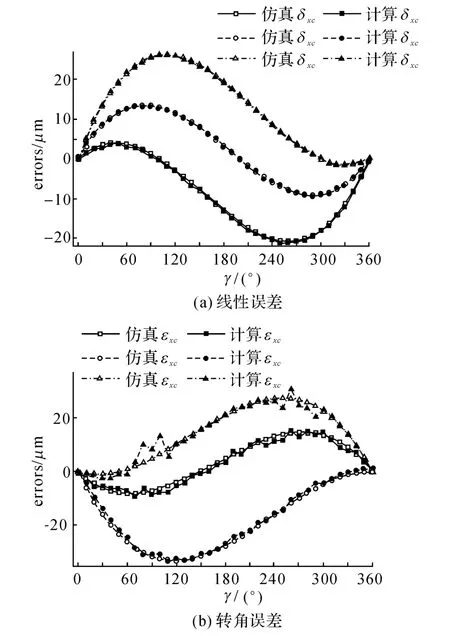
图5 转台6项基本误差项的仿真结果比较Fig.5 simulated results of six basic geometric errors

球杆仪公称长度公称长度远远大于球杆仪长度变化量，则球杆仪实际长度本身一个近似圆.对于步骤1-4，球杆仪刀具球的安装误差会造成球杆仪轨迹的偏心偏差，而工件球的安装误差主要影响球杆仪轨迹的半径.步骤5中球杆仪安装误差主要影响轨迹半径.步骤6中刀具球误差影响轨迹半径，而工件球是引起轨迹的偏心误差.如果已知球杆仪安装误差，那么从球杆仪实际读数中消除安装误差影响可表示为

式中：Δj′为第j 步骤中球杆仪实际读数.Δj为剔除球杆仪安装误差后球杆仪读数.j＝1，2…6.根据式（15）和（16）结合各个步骤中球杆仪实际读数，对球杆仪读数进行拟合.将式（15）代入（16）得到拟合形式为

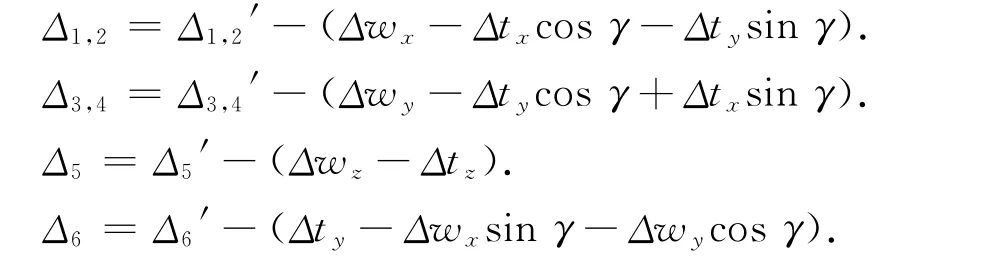
式中：Δj数值随着转角γ变化而变化，拟合式中只有球杆仪安装误差是常数项，根据最小二乘法进行拟合.球杆仪安装误差会远远大于机床的几何误差项，所以认为球杆仪长度本身近似圆的半径偏差都是由于球杆仪安装误差造成的，即最小二乘法拟合的常数项是由球杆仪安装误差造成的，从而拟合得到相应的球杆仪安装误差以及相应的剔除安装误差影响后的球杆仪数据.然后根据相应的辨识公式得到相应的10项几何误差.

这样六步骤测量法大大降低了球杆仪安装误差影响，提高了辨识精度，同时可以辨识得到转台10项几何误差.为了进一步提高辨识精度，每个步骤中安装球杆仪后进行多次测量得到多组球杆仪读数.该方法只需转台单独旋转，运动易实现，同时也消除了其他轴运动误差的耦合影响.步骤1，3和5的刀具球位置是一样的，而步骤2和4的刀具球位置是一样的，且都很容易通过机床定位得到，使得球杆仪安装很方便，提高了六圈法的测量效率，以达到快速测量的目的.

4 实 验

图6 球杆仪六步骤测量法测量转台误差Fig.6 Scenes of measurement for turntable using sixstep measurement with ballbar

将六步骤测量法应用到北京精雕SmartCNC500五轴机床上采用雷尼绍公司的QW20球杆仪测量辨识转台C 轴的几何误差.如图6所示为相应的六步骤测量转台误差示.图6（k）即为按照步骤k进行的测量.其中k＝1，2…6.步骤2和4中球杆仪刀具球z向高度L＝22mm.球杆仪安装方便.测量时只需转台单独旋转，机床很容易实现.转台旋转5°采集一次球杆仪数据，每个步骤安装球杆仪后进行5次测量，其平均值作为该步骤球杆仪读数测量值.如图7所示为各个步骤的球杆仪测量数据.根据球杆仪安装误差对各个步骤球杆仪测量数据的影响采用最小二乘法进行拟合，得到降低安装误差影响的球杆仪读数.然后根据六步骤测量法中各个误差辨识公式得到转台10项几何误差.表2为辨识得到的转台垂直度误差和位置误差.如图8（a）所示为转台三项线性误差，图8（b）为转台三项转角误差.

图7 六步骤测量法各个步骤球杆仪读数Fig.7 Ballbar readings of each step with six-step measurement

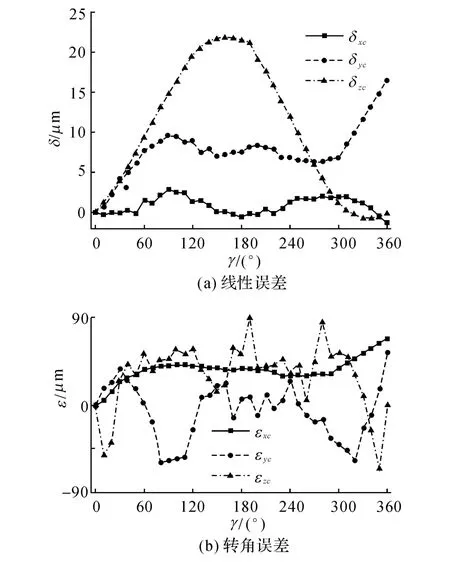
图8 辨识得到的转台6项基本误差项Fig.8 Six identified basic geometric errors of turntable

表2 转台垂直度误差和位置误差Tab.2 squareness errors and offset errors of turntable

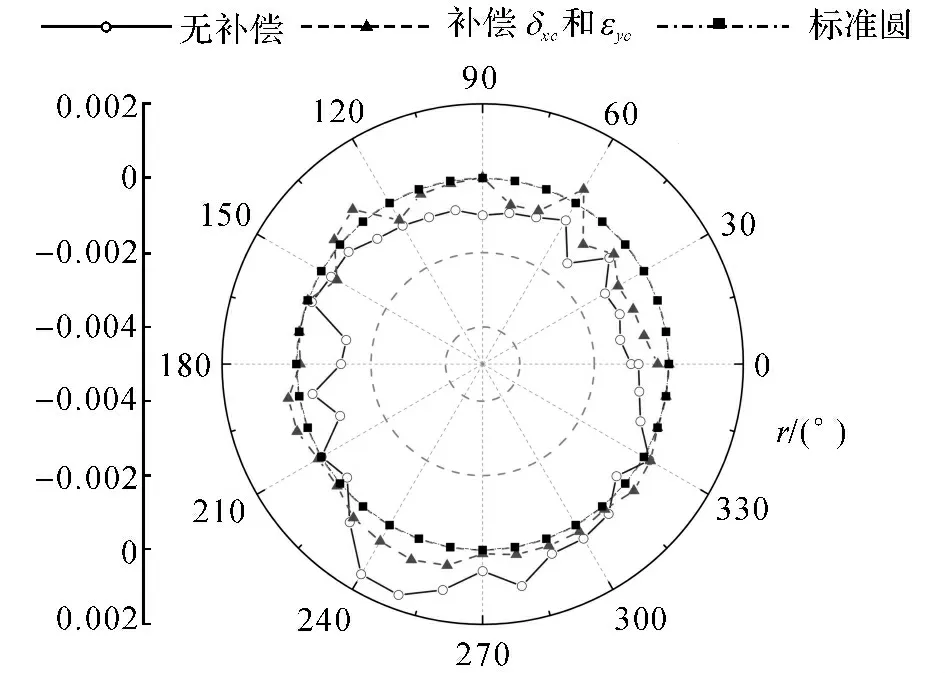
图9 步骤2中消除安装误差后球杆仪读数Fig.9 Ballbar readings of second step without set-up errors

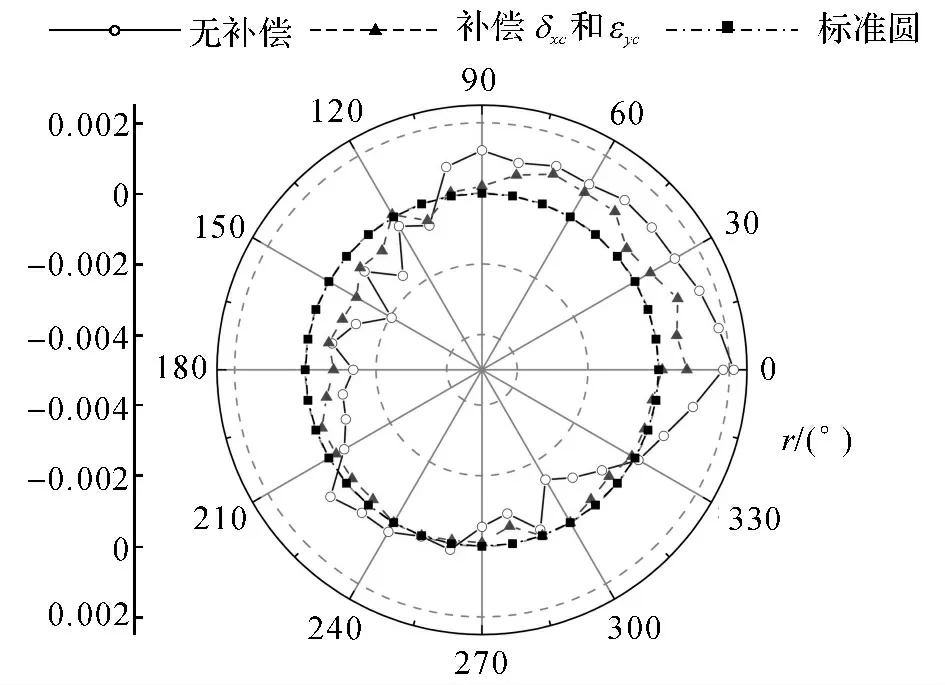
图10 步骤4中消除安装误差后球杆仪读数Fig.10 Ballbar readings of the fourth step without set-up errors

辨识得到的转台误差进行补偿，比较补偿前后球杆仪各个步骤处球杆仪读数来验证六步骤测量法的辨识精度.转台误差值可通过相应的平动轴来进行补偿.因为该方法是转台单独旋转，补偿是只是调整刀具球的坐标，这机床补偿代码也易实现，只需根据转台几何误差对机床精度的影响计算出刀具球位置调整值即可.比如步骤2中δxc，εyc，ocx和Scx影响机床精度，则可通过调整刀具球坐标值实现补偿.步骤4中δyc和εxc影响机床精度，则可通过X 轴和Y轴来调整球杆仪刀具球坐标来实现补偿.为了能够更清楚地观察补偿效果，将补偿前后球杆仪读数进行消除安装误差处理，得到消除安装误差影响后的球杆仪读数.如图9所示为步骤2中消除安装误差后补偿转台误差前后球杆仪读数比较图.如图10所示为步骤4中补偿转台相应误差前后球杆仪读数比较图.其中第3组数据为理想的标准圆轨迹读数，即零误差轨迹.消除安装误差后，步骤2 中误差从±1.6μm 减少到±0.7μm，补偿后误差值减少了56%，而且补偿后轨迹圆度大大提高.步骤4中误差从±2.1μm 减少到±0.8μm，精度提高了61.9%，补偿效果明显.那么进一步验证了六步骤测量法的辨识精度高.

5 结 论

旋转轴几何误差是影响五轴数控机床的主要因素之一，本文针对转台旋转轴提出了基于球杆仪的六步骤测量法来系统性的辨识得到十项几何误差项.六步骤测量法只需转台单独旋转，消除了其他运动轴几何误差对辨识精度影响，同时球杆仪安装方便，运动易实现.

（1）本文运用球杆仪方向向量将球杆仪读数和转台几何误差项结合起来.根据各个步骤中球杆仪方向向量，得到基本误差项辨识公式，同时结合几何误差项的性质，辨识得到包括垂直度误差和位置误差在内的十项几何误差项，并通过仿真验证六步骤测量方法的正确性.

（2）根据球杆仪读数模型，分析了球杆安装误差对各个步骤中球杆仪读数的影响，并采用最小二乘法根据球杆仪读数与安装误差进行拟合从而消除安装误差的影响，以提高辨识精度.

（3）将六步骤测量法应用到北京精雕SmartCNC500五轴加工中心，测量辨识得到C 轴的十项几何误差项，测量方便.同时通过补偿转台的几何误差对补偿前后球杆仪读数进行比较来验证六步骤测量法的可行性与准确性.

（

）：

［1］UDDIN M S，IBARAKI S，MATSUBARA A，et al.Prediction and compensation of machining geometric errors of five-axis machining centers with kinematic errors［J］.Precision Engineering-Journal of the International Societies for Precision Engineering and Nanotechnology，2009，33（2）：194-201.

［2］SHEN H，FU J，HE Y，et al.On-line Asynchronous Compensation Methods for static／quasi-static error implemented on CNC machine tools ［J］.International Journal of Machine Tools and Manufacture，2012，60（0）：14-26.

［3］CHEN G S，MEI X S，LI H L.Geometric error modeling and compensation for large-scale grinding machine tools with multi-axes［J］.The International Journal of Advanced Manufacturing Technology，2013，69（9／12）：2583-2592.

［4］WANG J，GUO J.Research on volumetric error compensation for NC machine tool based on laser tracker measurement［J］.Science China Technological Sciences，2012.55（11）：3000-3009.

［5］ZHU S，DING G，QIN S，et al.Integrated geometric error modeling，identification and compensation of CNC machine tools ［J］.International Journal of Machine Tools and Manufacture，2012.52（1）：24-29.

［6］FU G，FU J，XU Y，et al.Product of exponential model for geometric error integration of multi-axis machine tools［J］.The International Journal of Advanced Manufacturing Technology，2014.71（9／12）：1653-1667.

［7］FU G，FU J，XU Y，et al.Accuracy enhancement of five-axis machine tool based on differential motion matrix：Geometric error modeling，identification and compensation［J］.International Journal of Machine Tools and Manufacture，2015.89（0）：170-181.

［8］ZHANG Y，FU J Z，CHEN Z C.Machining tests to identify kinematic errors of machine tool table rotation axis based on sensitive directions［J］.The International Journal of Advanced Manufacturing Technology，2013.67（1／4）：495-500.

［9］LEI W T，HSU Y Y.Accuracy test of five-axis CNC machine tool with 3Dprobe-ball.Part II：errors estimation［J］.International Journal of Machine Tools ＆ Manufacture，2002.42（10）：1163-1170.

［10］TSUTSUMI M，TONE S，KATO N，et al.Enhancement of geometric accuracy of five-axis machining centers based on identification and compensation of geometric deviations［J］.International Journal of Machine Tools ＆ Manufacture，2013.68：11-20.

［11］TSUTSUMI M，SAITO A.Identification and compen-sation of systematic deviations particular to 5-axis machining centers［J］.International Journal of Machine Tools and Manufacture，2003.43（8）：771-780.

［12］ZARGARBASHI S H H，MAYER J R R.Assessment of machine tool trunnion axis motion error，using magnetic double ball bar［J］.International Journal of Machine Tools and Manufacture，2006.46（14）：1823-1834.

［13］LEE K I，LEE D M，YANG S H.Parametric modeling and estimation of geometric errors for a rotary axis using double ball-bar［J］.International Journal of Advanced Manufacturing Technology，2012.62（5／8）：741-750.

［14］LEE K I，YANG S H.Measurement and verification of position-independent geometric errors of a five-axis machine tool using a double ball-bar［J］.International Journal of Machine Tools and Manufacture，2013.70（0）：45-52.

［15］LEE K I，YANG S H.Robust measurement method and uncertainty analysis for position-independent geometric errors of a rotary axis using a double ball-bar［J］.International Journal of Precision Engineering and Manufacturing，2013.14（2）：231-239.

［16］ZHANG Y，YANG J，ZHANG K.Geometric error measurement and compensation for the rotary table of five-axis machine tool with double ballbar［J］.International Journal of Advanced Manufacturing Technology，2013.65（1／4）：275-281.

［17］CHEN J，LIN S，HE B.Geometric error measurement and identification for rotary table of multi-axis machine tool using double ballbar［J］.International Journal of Machine Tools and Manufacture，2014.77（0）：47-55.

［18］LIN Y，SHEN Y.Modelling of five-axis machine tool metrology models using the matrix summation approach ［J］.The International Journal of Advanced Manufacturing Technology，2003，21（4）：243-248.