基于梯形函数逼近的光栅数字细分算法

李 朋 高立民 吴易明

(中国科学院西安光学精密机械研究所1，陕西 西安 710119;中国科学院研究生院2，北京 100049)

0 引言

光栅码盘是一种精密测量角度信息的传感器，测量精度历来被视作衡量光栅码盘性能的一项重要指标。提高光栅码盘测量精度的方法有很多种。其中一种方法是通过提高光栅的刻划数量来实现，但由于现有工艺刻划水平的限制以及成本的制约，这种方法不作为提高光栅码盘精度的主流方法;另一种方法是对光栅码盘输出信号进行细分，这是目前常用的方法，如幅值分割法［1］、四倍频法［2］、互补函数法［3］、电阻链法［4］以及锁相倍频细分法［5］等。虽然这些方法都可以达到细分的目的，但存在很多缺点，如四倍频法细分过程简单，但细分倍数比较低;幅值分割法细分精度高，但算法占用的存储空间大。

梯形函数逼近一般用于求解函数值，目的是简化计算过程。它用折线来拟合已知函数，可以很容易地计算出结果。计算过程无需查表，节省了存储空间，只要逼近步长选择得当，就可以达到很高的精度。

1 梯形函数逼近原理

在理想状况下，从光栅码盘输出的四路信号经差分放大后得到两路正交的正弦信号［6］，即:

现在假设用采样脉冲对两路信号进行采样，得到的光栅信号如图1所示。

图1 光栅信号Fig.1 Grating signals

上升沿触发，第i个采样脉冲所对应的幅值为Asinxi，假设在第(i+1)个上升沿到来时所走过的相位为dxi，那么第(i+1)个脉冲所对应的正弦波的幅值应为Asin( xi+dxi)。

由于采样脉冲的频率很高、dxi很小，对其采用梯形公式逼近，得到:

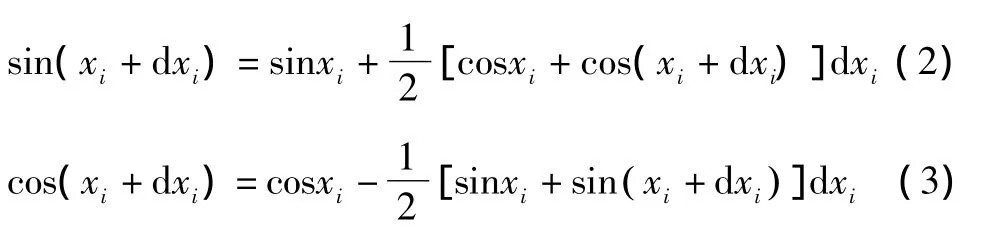
此处振幅A并不影响展开，因此不予以考虑。由于sin( xi+dxi)、sinxi、cosxi以及 cos(xi+dxi)都可以由采样得到，因此，式(2)、式(3)其实是关于dxi的一阶方程。

由式(2)、式(3)可以分别求得dxi:

每经过一个脉冲采样就会得到一个dxi值。假设经过了N个脉冲采样，则可得波形所走过的总相位为:

2 细分算法的具体实现

2.1 光栅信号频率的确定

光栅信号采样频率决定着细分算法的精度，如果采样频率太低，就会造成光栅信号信息的丢失，使细分误差较大。

不同采样频率时的细分误差如图2所示。

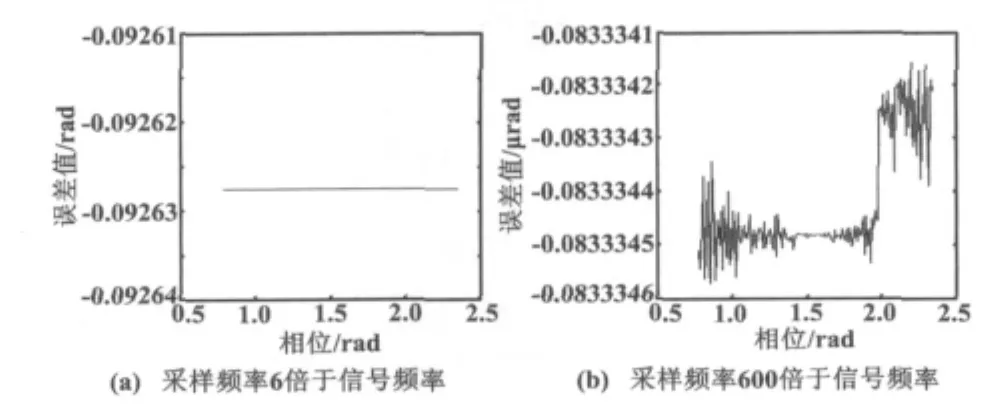
图2 不同采样频率时的细分误差Fig.2 Subdivision error under different sampling frequencies

虽然采样频率越高、光栅信号信息就越不容易丢失，但采样频率也不是越高越好。因为采样频率越高，信息量就会越大，要求的数据处理周期就会越短。

通常芯片数据处理速度都是确定的，这也决定了光栅信号频率和采样频率的上限。如采用浮点运算单元(float point unit，FPU)做一次加法或减法运算需要七个时钟周期，做一次除法运算需要35个时钟周期。如果芯片时钟频率为100 MHz，那么用此算法做一次细分运算就要使用57个时钟周期，大约0.57 μs。为了保证运算时间充足，将每次运算的时间设定为1 μs，则数据处理的频率为1 MHz。

同时，为了保证细分精度，假设对每个波形至少采样13个点，那么对应的光栅信号频率就不能超过77 kHz。如果信号频率超过77 kHz，就会出现丢数现象，这在一定程度上带来了运算误差，从而影响测量精度。

2.2 细分算法区间的划分

虽然直接利用式(4)、式(5)可以求解dxi的值，但是所得到的结果是近似值，并不是真实值，它们之间存在着一定的误差，而且在某些点还会出现小数除大数的情况，如式(4)在 π/2和3π/2处、式(5)在0和 π处，这会引起较大的细分误差。

为使除数不出现极小值，对式(4)和式(5)分以下两种区间应用:在区间(－π/4+kπ，π/4+kπ)时调用式(4)，在区间(π/4+kπ，3π/4+kπ)时调用式(5)。对于区间边界点，即当两个采样点不在同一区间时，由第二个边界点来决定。这样通过区间划分来选取对应细分公式，可以很好地提高测量精度，消除较大误差点。

2.3 数据处理

由于累加法存在误差积累的固有缺陷［7］，因此必须对数据处理作一点修正。由前文可知，当信号波形被划分为两种区间后，每种区间的相位长度为π/2 rad。因此，可将数据处理公式写成:

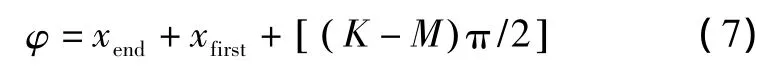
式中:前两项为精码部分，分别表示最后一个区间和第一个区间所转过的相位;第三项为粗码部分，代表转过的区间数，K为正转区间数，M为反转区间数。

在计算过程中，因为每个计算区间的相位长度为π/2 rad，所以当一个完整的计算区间计算完毕后其结果只会是π/2或－π/2。但由于外界干扰或光栅自身刻划的影响［8－9］，计算结果可能不是 π/2 或 － π/2，只是接近π/2或－π/2，所以规定计算完一个完整的计算区间后，不论这一个区间的计算结果如何，都进行强制赋值。如果此区间计算结果在π/2邻域内(对于邻域半径可以根据试验环境设定)，则强制计算结果为π/2;在计算结果在－π/2邻域内，则强制计算结果为－π/2。在计算完毕一个区间后，根据计算值来决定K和M是否加1，然后令计算值归零，开始新一轮计算。这样由叠加所引起的误差累积现象就被控制在一个计算区间内，基本可以忽略。

3 误差分析

前文已提及理想波形下算法所带来的误差，此处主要讨论波形不理想情况下所引起的误差。所谓波形不理想主要是指从光栅码盘出来的两路信号幅值不相等或相位不正交。

假设所获得到的两路信号差分放大后为:

针对式(8)，下面分两种情况进行讨论。

①当A0=A1、δ不为0时，将采集到的值代入式(4)，可得:

令 dxi=0.1 rad，δ分别取 0.1 rad、0.01 rad、0.001 rad时，可以计算得到 π/2区间内的 dxi，误差值为 ( d xi－d)。(－π/4～+π/4)区间内的细分误差如图3所示。

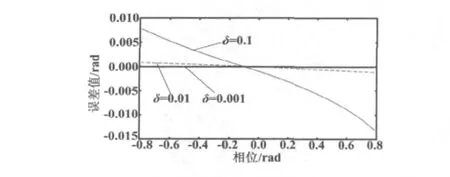
图3 信号非正交所引起的细分误差Fig.3 Subdivision error caused by non-orthogonal signals

从图3可以看出，δ越大，它引起的计算误差越大，且误差在一个计算区间内是关于区间中点近似对称的。因此，在一个完整的计算区间内，由于正负叠加，δ的影响是不断减小的，其最大误差只会出现在前半个计算区间或后半个计算区间。现在假设 δ=0.1 rad、dxi=0.1 rad，那么在π/4 rad区间内的采样点为八个，引起的计算误差大约为0.08 rad，约为两个采样点间的相位差大小。因此，对整个精度来讲并不会有多大影响。但是如果δ很大，就不能忽略其影响，此时需要有一个相位补偿电路［10］。

② 当 δ=0、A0≠A1时，式(4)、式(5)分别为:

4 试验仿真

为验证算法的精度，在Matlab平台下对算法进行仿真试验。

设采样步距角在0.02～0.20 rad之间，并每隔0.02 rad进行一次仿真，每次仿真设为100步。梯形函数逼近法细分结果如表1所示。

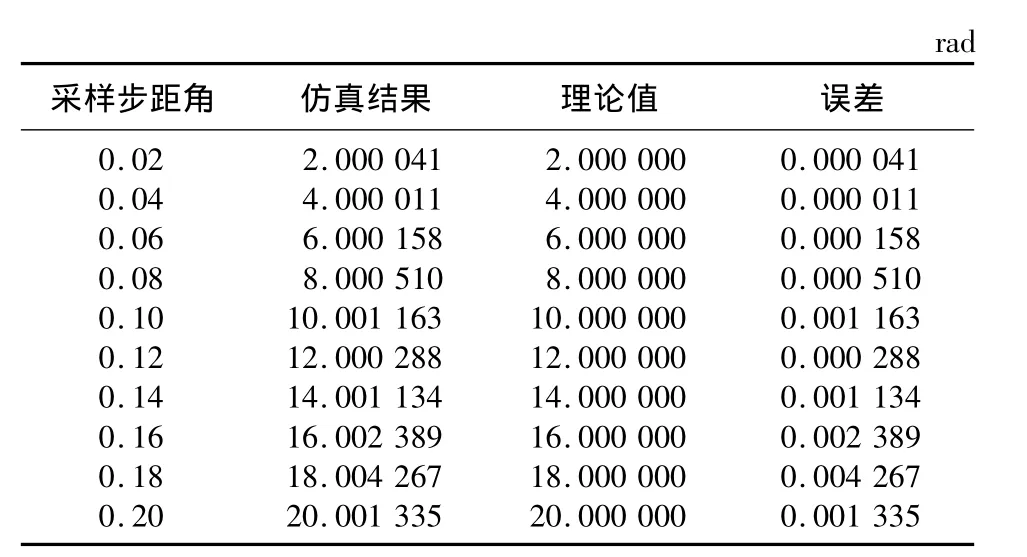
表1 细分结果Tab.1 Subdivision results

从表1可以看出，梯形拟合算法的细分精度较高。

5 结束语

综合以上分析可以看出，梯形函数逼近数字细分法计算简单，而且其精度仅与信号频率和采样频率有关，采样频率越快，精度越高。同时，梯形函数逼近数字细分法不需要辨向电路［11－13］，这大大简化了电路设计过程，并且可以在一定程度上消除由相位不正交所引起的误差，提高了测量精度。

［1］罗华，高山，李翔龙.粗光栅信号全数字化处理法实现高倍数细分［J］.光学精密工程，2007，15(2):283 －288.

［2］王度桥，刘勇，周岗，等.光电码盘脉冲信号四倍频检测方法的分析与研究［J］.航电技术，2009，29(8):14 －17.

［3］徐从裕，余晓芬.基于互补函数算式的光栅快速细分方法［J］.电子测量与仪器学报，2006，20(3):6－9.

［4］张兴华，王克逸.光栅信号电阻链高倍细分法的误差校正的研究［J］.电子测量技术，2008，31(7):35 －39.

［5］郭雨梅，崔晋玲，刘雪艳，等.锁相式莫尔条纹信号细分方法［J］.哈尔滨工业大学学报:工学版，2007，39(9):1496－1498.

［6］唐小琦，刘世峰，王平江，等.正切法莫尔条纹信号幅值分割细分的误差分析［J］.计量学报，2007，7(3):220 －223.

［7］陈赟，张红胜.光电轴角编码器的编码方式及其发展趋势［J］.中国光学与应用光学，2009，2(2):126－133.

［8］陈赟.曝光量对码盘、圆光栅均匀性误差的影响［J］.计量技术，2005(12):28－29.

［9］黄宗升，秦石乔，王省书，等.光栅角编码器误差分析及用激光陀螺标校的研究［J］.仪器仪表学报，2007，28(10):1866 －1869.

［10］吕孟军，郭琪，吕印晓.莫尔条纹信号相位误差补偿［J］.光学精密工程，2009，17(7):1694 －1700.

［11］蒋晶，蒋东方，高航.高可靠性增量式光电编码器接口电路设计［J］.测控技术，2009，28(2):1 －4.

［12］李拥军，范永坤，杨辉.光电编码器滤波技术研究［J］.自动化仪表，2008，29(7):21 －23.

［13］孙祥明，齐明侠，沈蓉.编码器换向误码输出原因探讨及鉴相电路改进［J］.石油大学学报:自然科学版，2004，29(4):91 －94.