模糊内模PID控制及应用

陆 平 赵 捷 郭 鹏

(南通大学电气工程学院1，江苏 南通 226019;中国农业大学水利与土木工程学院2，北京 100083)

0 引言

时滞现象在工业生产控制系统中普遍存在，这使得系统的控制变得非常困难［1］。多年来，不少学者对时滞系统的控制方法进行了研究，如模糊PID控制［2］、神经网络控制［3］、预测控制［4］、Smith 预估控制［5］、内模控制［6］等。这些方法已经大部分应用到工业生产过程中，并取得了一定的经济效益。对于被控对象含有非线性环节的情况，有人提出了在线辨识的方法［7］，但目前的研究大多仍停留在仿真阶段。针对非线性时滞系统，本文采用模糊内模PID控制方法进行控制，并将这种方法运用到JX-300X DCS温度系统中。运行结果证明了该方法的可行性。

1 内模控制的基本原理

内模控制在结构上与Smith预估补偿很相似，它有一个被称为内模的过程模型，控制器的设计可由过程模型直接求取。

内模控制原理如图1所示。

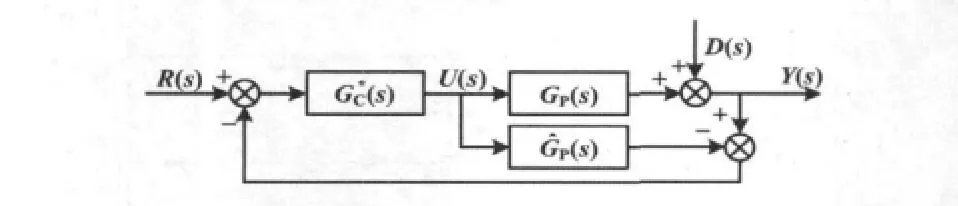
图1 内模控制原理图Fig.1 Schematic of internal model control

图1中:GP(s)为被控对象;(s)为内模(s)为内模控制器;D(s)为外界扰动;R(s)为设定值。

1.1 理想的内模控制器

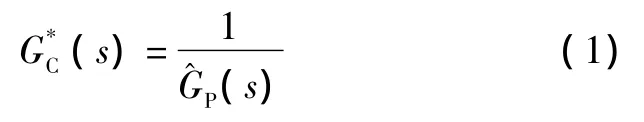
可见，当GP(s)可倒时(s)能克服外界扰动。

② 当R(s)≠0、D(s)=0时，Y(s)=R(s)。可见，(s)是Y(s)跟踪R(s)的理想控制器。

1.2 实际的内模控制器

理想的内模控制器是在“模型没有误差且可倒”的情况下得到的。在实际工作中，模型与各种不同工况下的实际过程总会存在误差，且(s)有时不可倒。因此，实际的内模控制器必须在理想控制器的基础上加以改进。

实际内模控制器的设计可分为两个步骤。

步骤1，将过程模型做因式分解:

步骤2，控制器设计:

这里的f是静态增益为1的低通滤波器，其典型形式为:

式中:Tf为内模控制器的设计参数，Tf的大小决定了控制系统的响应速度;参数r为一正整数。

2 PID参数的整定

利用内模原理整定PID参数时，可从以下两个方面入手:①将内模控制器转化为反馈控制器的形式，再将反馈控制器转化为选定的PID控制器;②整定滤波器常数Tf，使控制系统兼顾鲁棒性和控制性能。

考虑到大部分工业控制对象可近似地用一阶惯性环节来表示，假设其开环传递函数为:

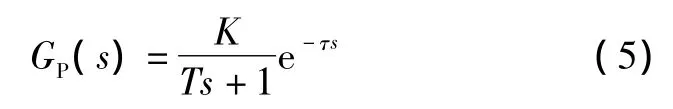
基于内模原理的PID控制器为:

式中:KC、TI、TD分别为控制器的放大倍数、积分时间和微分时间。PID参数控制器的整定公式如下。

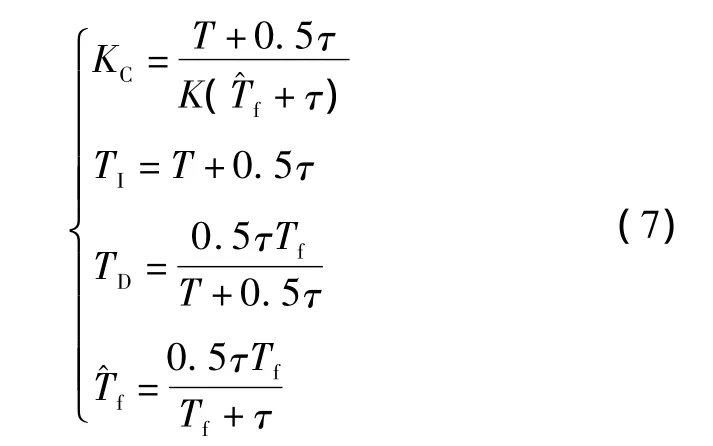
由式(7)可知，控制器的三个参数只与滤波器的时间常数Tf有关，因此，只需调整参数Tf。

3 温度系统的建模

对于任何一个控制系统，如果能事先知道系统的模型，这对控制量的计算大有好处。在工业生产过程中，系统的参数往往不断发生变化，要想实时跟踪系统的参数，就必须采取在线辨识的方法［9］。在线辨识的方法很少能运用到工业生产系统中，这是因为在线辨识得到的参数往往偏离真实参数，甚至产生发散现象。如何在避免在线辨识不精确性的同时，根据系统运行的实际情况实时地调整系统参数是值得研究的内容。

既然在线辨识比较困难，则可考虑离线辨识。以电加热炉为例，通过进一步分析可以发现，该系统的开环传递函数主要受液位高度、流量、温度初始值及设定值、液体的种类等因素的影响。如果考虑以上各种因素，则需要离线辨识大量的系统参数，工作量将会很大。为了减少离线辨识的工作量，可以考虑影响系统参数的主要因素，在此以液位高度、温度初始值及设定值为例，研究温度系统的离线辨识。

离线辨识可采用以下方法进行。假设液位高度为H、温度为t1时，用于控制加热炉电压的晶闸管开度为a%，将晶闸管开度增加到(a+Δa)%，则系统的温度会上升，设稳定后的温度为t2。根据开环响应曲线，通过作图法即可确定这种情况下的系统模型。

下面研究系统参数的变化情况。首先研究液位高度对参数的影响，假设电加热炉中液位的最高值为300 mm，可以将高度分为若干部分。若每60 mm为一段，则液位最高值可分为5段。在每一段内可将该段中点值作为建模的液位高度。假如液位在180～240 mm之间时，则以210 mm作为建模时的液位高度。对温度也做类似的处理，若初始值为常温20℃，设定值的最高值为100℃，则温度可分为以下4段:20～40℃、40～60℃、60～80℃、80～100℃。在每段建模时，也以该段中间值作为建模时的实际值。

由上文的分析可知，如果考虑液位高度以及温度初始值和设定值的影响，需要离线建立5×4=20个模型。可以推知，如果考虑更多的影响系统参数的因素，将需要离线建立更多的模型。事实上，在实际控制系统中，有些因素的变化范围事先是已知的。当有扰动时，液位高度在180～220 mm之间波动、温度在60～85℃之间波动。如果这些因素的变化范围已知，就不需要建立那么多模型，而是根据实际情况，将每段的范围减小，以提高每段参数的精度。当已知液位高度在180～220 mm变化时，为使建立的模型更加精确，可将其分为以下两段:180～200 mm、200～220 mm。当然，作为一个功能较强的控制软件，要能适应较宽范围的参数变化，事先建立较多的系统模型还是十分必要的。

系统的传递函数可由式(5)来表示，需要辨识的参数为K、T、τ。利用离线辨识，得到一系列工况下系统的传递函数后，就可利用模糊内模PID进行控制。

4 模糊内模PID原理

已知每一种情况下的系统开环传递函数，由式(7)可求得控制器中的每一个变量。假设液位的高度为h，温度为t，可借助基于T-S的模糊控制器来确定液位高度、温度设定值与中的每一个变量之间的关系［10］。以KC为例，当h1＜h＜h2、t1＜t＜t2时，根据离线辨识得到的系统参数以及式(7)计算得到PID控制器的比例系数为K'C，则可得到如下的模糊规则:

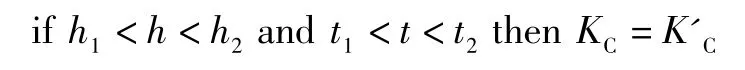
同理，根据式(7)可得到液位的高度h、温度t与TI、TD之间的关系。求得每一种情况下的KC、TI、TD后，可将它们代入式(6)，得到这种情况下PID控制器的表达式。实际运行时，系统根据测得的温度t以及液位高度h，实时地调用相应的PID控制器，对温度系统进行控制。基于模糊内模PID控制的温度系统的原理图如图2所示。

图2 模糊内模PID温度系统原理图Fig.2 Schematic of temperature system based on fuzzy internal model PID

图2中:t为锅炉液体的温度;h为液位的高度。

5 应用举例

JX-300X是浙大中控生产的DCS系统，它可对液位、温度、流量等进行研究。它的基本组成包括工程师站(ES)、操作站(OS)、控制站(CS)和通信网络 SCnet II.。该系统非常接近于工业生产实际系统。在编程前，先对系统流程进行组态，并定义控制变量。

JX-300X系统提供了一套被称为SCX语言的编程软件，其中包含一些模块指令，如一阶滞后模块、纯滞后模块、PID控制模块和多路切换模块等，这些模块指令降低了编程的难度。如当参数已知时，只需调用PID模块和一阶滞后模块，就能实现的功能。

通过观察JX-300X DCS系统运行后的监控画面可以发现，当温度设定值和液位高度发生变化时，由于能够及时调整系统开环传递函数并修正PID参数，电加热炉的温度能迅速地跟踪设定温度且几乎没有超调，取得了较好的控制效果。

6 结束语

在流程工业中，工业控制对象或多或少地存在时滞环节、非线性环节，常规控制方法很难满足控制要求。内模PID控制能较好地克服时滞环节对系统控制的影响，但系统参数变化较大时，控制效果将会下降。在线辨识是研究得较多的系统参数辨识方法，但这种技术很少能够应用到实际工程中。文章提出了离线辨识系统参数，采用模糊内模PID控制的方法，以适应系统参数的变化。将这种控制方法运用到DCS温度系统中，取得了令人满意的控制效果。

［1］王树青.工业过程控制工程［M］.北京:化学工业出版社，2007.

［2］张莉.混合模糊PID控制器在伺服控制系统中的应用［J］.自动化仪表，2010，31(6):61 －63.

［3］谢光辉，喇凯英，王留运.液压机械补偿功率回收模型参考模糊神经网络控制［J］.机床与液压，2009，37(2):114 －116.

［4］孙优贤.工业过程控制技术［M］.北京:化学工业出版社，2006:48－107.

［5］夏晴，夏扬，郑伟建.基于Smith预估的自抗扰控制系统［J］.计算机仿真，2009，26(7):168 －171.

［6］尚继良，王晓燕，于玮.内模控制在锅炉燃烧系统中的应用研究［J］.微计算机信息，2007，23(12－1):41－42.

［7］李耀凯，王建，任永平.空调系统的温度控制和在线辨识［J］.装备指挥技术学院学报，2011，22(1):104－106.

［8］黄岩.多变量内模-PID控制［D］.北京:北京化工大学，2008.

［9］周远平，孙亚萍.定子参数在线辨识技术的研究［J］.微特电机，2010(8):18－21.

［10］赵宏伟，齐一名，臧雪柏，等.基于系统辨识与T-S模糊神经网络的磨矿分级控制［J］.吉林大学学报:工学版，2011，41(1):171 －175.