相干干扰下无源测向系统方位测量误差模型
2012-12-01杨军佳毕大平张国利
杨军佳,毕大平,2,张国利
(1.解放军电子工程学院,安徽 合肥 230037;2.安徽省电子制约技术重点实验室,安徽 合肥 230037)
0 引言
凭借信号方位角测量的隐蔽性和精确性,无源测向系统已成为当今必不可缺的军事侦察手段,为此,对该系统干扰技术以及干扰效果评估的研究具有一定的军事意义。对无源测向系统进行相干干扰是使干扰源与辐射源发射相同(或参数相似性很高)的信号同时进入无源测向系统以达到降低该系统效能的目的。目前关于提高无源测向系统的测向精度[1-2]以及影响无源测向系统测向精度因素[3-5]的研究比较多,而对无源测向系统进行主动干扰以及干扰效果评估的研究几乎还没有。为了定量评估相干干扰对无源测向系统产生的干扰效果,本文推导了在相干干扰下两种典型的无源测向系统对信号方位的测量误差。
1 无源测向原理
无源测向技术包括幅度法和相位法两种,其中幅度法测向又可分为搜索法测向和比幅法测向,而相位法测向主要是相位干涉仪测向。
1.1 比幅法测向的原理
比幅法测向原理是用多个独立、主瓣波束毗邻的天线覆盖特定的方位,对同一辐射源信号来说,总有一对相邻波束分别输出最强和次强信号,通过比较这对相邻波束输出信号包络幅度的大小,来确定信号的方向[6]。该测向系统的相邻天线方向图可用图1表示。
为了讨论方便,假设辐射源和天线阵在一个平面内,且与各天线相连的各接收通道性能完全一致。若有一平面电磁波从天线等增益轴夹角θ方向到达两相邻天线1和2,且两相邻天线波束最大增益方向夹角为Θ,则信号经过相应接收机通道的射频放大、检波及对数放大后的信号幅度差ΔU为:
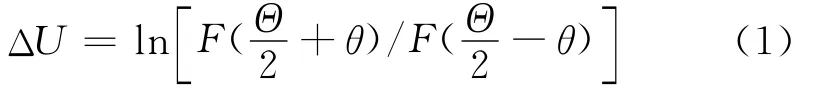
而单元天线的方向图函数可用高斯函数近似[5-7],即
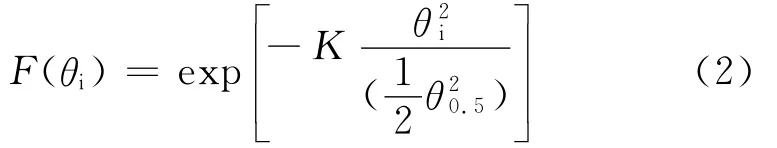
式(2)中,θi为来波信号与天线波束最大增益方向的夹角,θ0.5为天线半功率波束宽度,K为比例常数。
由式(1)、式(2)可得辐射源信号的到达方向θ为:
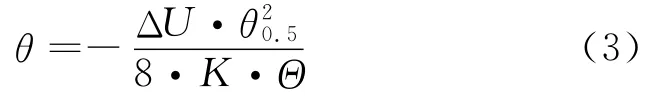
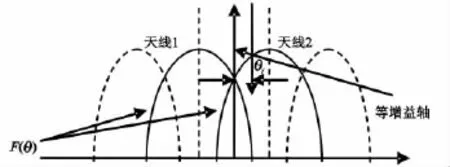
图1 比幅测向天线方向图示意图Fig.1 The schematic diagram of amplitude-comparison direction finding antenna
1.2 比相法测向的原理
最简单的单基线相位干涉仪由两个信道组成,如图2所示。

图2 一维单基线干涉仪原理图Fig.2 The schematic diagram of one-dimensional and single-baseline interferometer
为了讨论方便,假设辐射源和天线阵在一个平面内。若有一平面电磁波从天线视轴夹角θ方向到达天线1和2,则天线接收到的信号相位差φ为:

式(4)中,λ为信号波长,d为两天线间距。
若两信道的相位响应完全一致,接收机输出的信号相位差仍然为φ,经鉴相器取出的相位差信息,再进行角度变换,求得辐射源信号的到达方向θ:

1.3 相干干扰机理
干扰设备发射与雷达辐射源信号有相同的载频和脉冲参数的干扰信号,通过与被保护辐射源的协同达到同时工作,保证干扰信号和辐射源信号同时进入无源测向系统。无源测向系统依据测向原理对两相干信号进行处理,从而得出虚假的辐射源方位信息。各设备配置可用图3表示。

图3 干扰设备与辐射源配置示意图Fig.3 The diagrammatic sketch of the location of jamming equipment and radiation source
图3中,干扰信号入射方向与比幅测向系统天线等增益轴(比相测向系统干涉仪法线)夹角为θj,辐射源信号与比幅测向系统天线等增益轴(比相测向系统干涉仪法线)夹角为θs,干扰信号与辐射源信号到达测向天线距离分别为Ra、Rb(即两信号到达无源测向系统的相位差Δφ=2π(Ra-Rb)/λ),无源测向系统测得的辐射源信号与比幅测向系统天线等增益轴(比相测向系统干涉仪法线)夹角为θi。
2 相干干扰下无源测向系统方位测量误差模型
为研究方便,假设辐射源信号与干扰信号均为正弦信号,干扰信号与辐射源信号初始相位差为φo,干扰信号与辐射源信号的幅度分别为Aj和As,忽略信号传输损耗、极化损耗等。各设备配置如图3所示。
2.1 相干干扰下比幅法测向系统方位测量误差模型
假设比幅测向系统中各天线的方向图及接收通道性能一致,则依据比幅法测向原理可得两相邻天线接收到的信号为:

式(6)中,S(t)、S′(t)分别为两相邻天线接收到的辐射源信号与干扰信号的和信号,其余参数同上。
由比幅法测向原理及式(1)可得:

由式(3)、式(7)可得,在相干干扰情况下比幅法测向系统测得的信号方位角为:

式(8)中,η=Aj/As,其余参数同上。于是可得相干干扰下比幅法测向系统方位测量误差为:

由式(9)可看出,比幅法测向系统测得的信号方位测量误差与测向系统接收到的干信比及干扰信号入射角(θj)有关。
2.2 相干干扰下比相法测向系统方位测量误差模型
假设干涉仪为最简单的单基线相位干涉仪,其两天线之间的基线长度为d。依据相干信号之间矢量合成的原理,当两相干信号同时进入干涉仪两天线时,其示意图如图4所示。图中,实线箭头是雷达信号方位,长虚线箭头是干扰信号方位,而点虚线箭头是雷达信号与干扰信号进行矢量合成后的虚假辐射源信号方位(即干涉仪测得的假信号方位)。
为方便进行矢量合成分析,我们把正弦信号用矢量形式来表示,则相应的辐射源信号Ss与干扰信号Sj分别为:
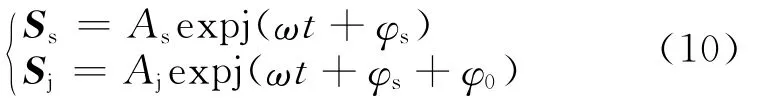
则两信号到达两接收机1、2输出端的和信号S1、S2分别为:
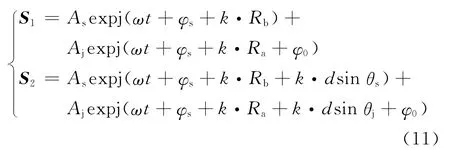
式(11)中,k=2π/λ,其余参数同上。
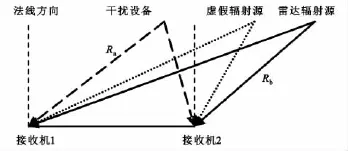
图4 干涉仪接收两相干信号示意图Fig.4 The diagrammatic sketch of interferometer receiving two coherent signals
由式(11)可得两接收机输出端和信号的相位差Δφ为:

式(12)中,φ1=k(Ra-Rb)+φ0,φ2=φ1+kdsinθj-kdsinθs,η=Aj/As。
由式(5)、式(12)可得,在相干干扰情况下比相法测向系统测得辐射源信号方位角为:
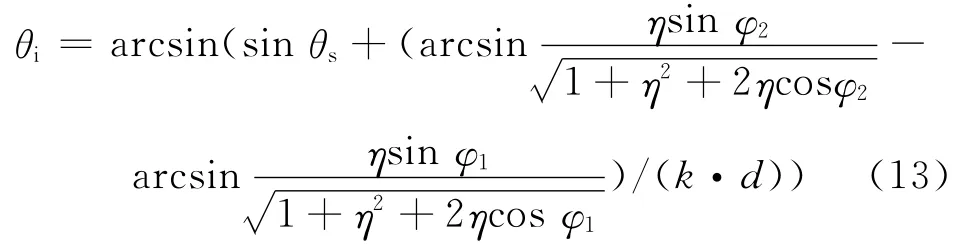
于是可得相干干扰下比相法测向系统方位测量误差为:

式(14)中,各参数同上。
由式(14)可知,比相法测向系统方位测量误差与测向系统接收到的干信比以及干扰信号入射角有关。
3 方位测量误差仿真分析
为了便于讨论且不失一般性,本文考虑8元天线阵全向比幅测向系统(Θ=45°)以及单基线干涉仪测向系统(两基线间隔d=0.1m)。天线方向图函数中K=0.693,半功率角θ0.5=60°,辐射源信号与干扰信号波长都是0.2m,雷达信号入射角θs=10°,辐射源信号与干扰信号初始相位差φo=0°。仿真过程中,忽略信号的传输损耗、极化损耗以及系统本身的测量误差。根据上述分析对相干干扰下无源测向系统方位测量误差仿真如图5、图6所示。
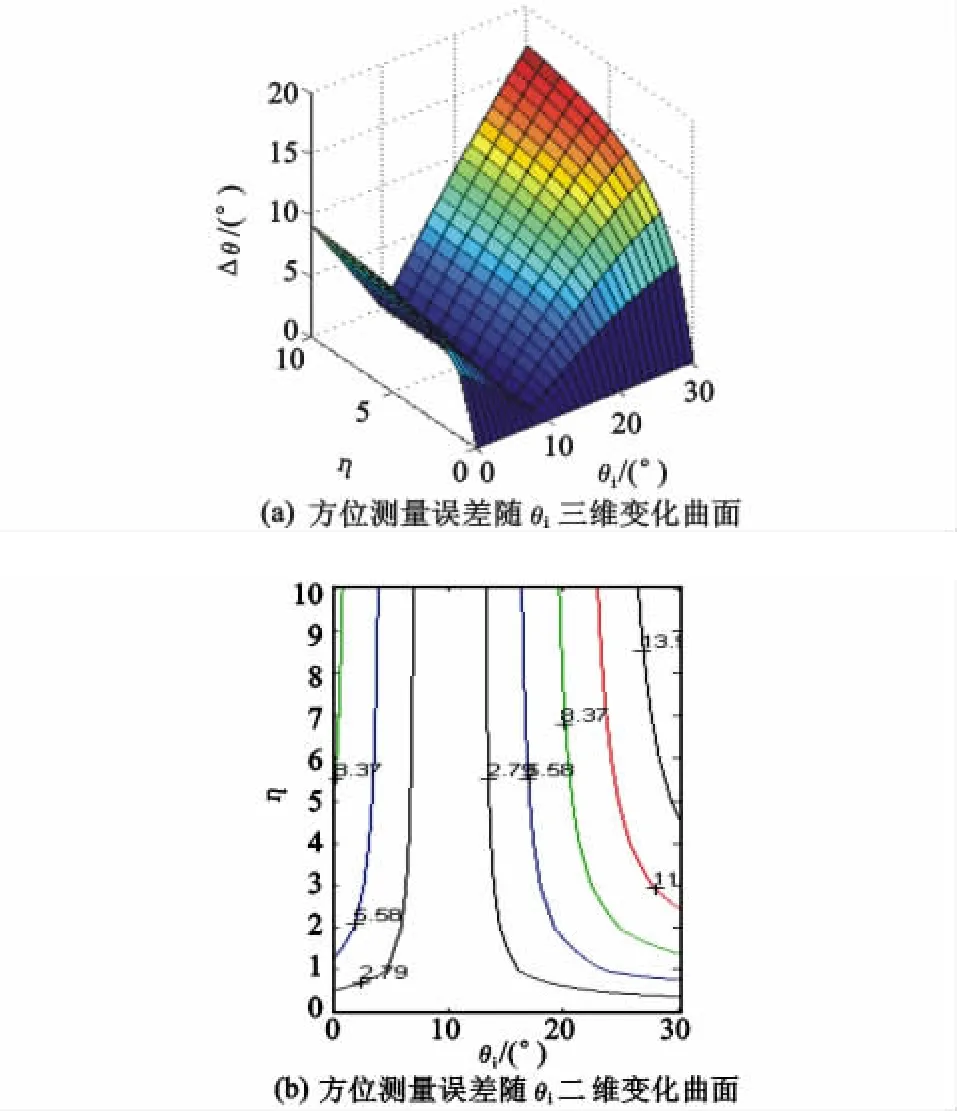
图5 比幅法测向系统方位测量误差变化曲线Fig.5 The changing curve of direction-finding error of amplitude-comparison direction finding system

图6 比相法测向系统方位测量误差变化曲线Fig.6 The changing curve of direction-finding error of phase direction finding system
由图5和图6可知:
1)相干干扰下,两种典型的无源测向系统方位测量误差的变化趋势是一致的,且方位测量误差都是来自于两个方面:测向系统接收到的干信比以及干扰信号、辐射源信号与测向系统所交汇成的夹角。当测向系统接收到的干信比一定的情况下,方位测量误差随着干扰信号、辐射源信号与测向系统所交汇成的夹角的增大而增大;当干扰信号入射角以及辐射源信号入射角一定的情况下,无源测向系统的方位测量误差随着接收到的干信比的增大而增大。
2)当无源测向系统接收到的干信比为零时,方位测量误差为零;当干扰信号入射角与辐射源入射角相同时,方位测量误差为零。
上述方位测量误差变化趋势的仿真分析与常理是相符的:
1)针对比幅测向系统,当干扰信号功率为零或者干扰信号入射角与辐射源信号入射角相同时,无源测向系统的方位测量误差为零,这是显然的;当干扰信号入射角、辐射源信号入射角一定的情况下,干信比越大,比幅测向系统测得的方位角越偏向于干扰源,例如,当干信比远远大于1时,测向系统测得的方位角为干扰信号入射角,当干信比远远小于1时,测向系统测得的方位角为真实的辐射源信号入射角;当测向系统接收到的干信比一定的情况下,干扰信号、辐射源信号与测向系统的夹角越大,比幅测向系统测得的方位角越偏离辐射源入射角,例如,当干扰信号入射角与辐射源信号入射角关于等增益轴对称时,测向系统测得的方位角为零,当干扰信号入射角与辐射源信号入射角相同时,测向系统测得的方位角为真实辐射源信号入射角。
2)针对比相测向系统,两相干信号进行矢量合成,如图7所示。

图7 两矢量合成示意图Fig.7 The diagrammatic sketch of two vectors composing
当其中一个矢量的模为零或者两矢量之间的夹角为零时,其和矢量与另一个矢量同向,这是显然的;当其中的一个矢量固定之后,和矢量随着两个矢量之间夹角的增大而偏向于另外一个矢量;和矢量随着另一个矢量模的增大与固定的矢量之间的夹角也是越来越大的。
4 结论
本文推导了无源测向系统在相干干扰下的方位测量误差公式,该公式首次描述了相干干扰对无源测向系统方位测量的影响。依据文中的分析,相干干扰下无源测向系统的方位测量误差的变化趋势与常理是相符的,从而说明了该模型的有效性。文中推导的相干干扰下无源测向系统的方位测量误差模型没有考虑测向系统本身的测向误差以及随机测量误差等因素,且该误差模型没有经过实际数据的验证,下一步将对该误差模型进行完善和实验验证。
[1]赵勇慧.提高相位干涉仪测向精度与改善测角范围的探讨[J].火控雷达技术,2002(2):34-37.ZHAO Yonghui.Discussion on increase of direction accuracy and angle range of phase interferometer[J].Fire Control Radar Technology,2002(2):34-37.
[2]翟庆伟,王玉,宫兵.波束比幅法测向技术研究[J].无线电通信技术,2007,33(6):55-56.ZHAI Qingwei,WANG Yu,GONG Bing.Research on the technology of the beam amplitude comparison direction finding[J].Radio Communications Technology,2007,33(6):55-56.
[3]谢飞,张忠臣,张鹏.多径效应对测向误差的影响[J].电子测量技术,2010,33(1):29-31.XIE Fei,ZHANG Zhongchen,ZHANG Peng.Influence on direction finding error by multipath effect[J].Electronic Measurement Technology,2010,33(1):29-31.
[4]毛虎,杨建波,邱宏坤.多径效应对信号接收及方向测量的影响[J].电讯技术,2010(10):63-68.MAO Hu,YANG Jianbo,QIU Hongkun.Influence of multipath effect on signal receiving and direction finding[J].Telecommunication Engineering,2010(10):63-68.
[5]李鹏,武胜波.比幅法测向及其误差分析[J].电子元器件应用,2009,11(10):89-92.
[6]罗景青.雷达对抗原理[M].北京:解放军出版社,2003.
[7]王有朝.比幅测向动态范围的分析与测试[J].现代雷达,2006,28(8):50-53.WANG Youzhao.Analysis and measurement of dynamic range of amplitude-comparison df equipment[J].Modern Radar,2006,28(8):50-53.
