弹丸侵彻混凝土目标减加速度信号的处理原则

范锦彪，祖 静，徐 鹏，王 燕

（1.电子测试技术重点实验室，山西 太原 030051；2.仪器科学与动态测试教育部重点实验室，山西 太原 030051；3.中北大学信息与通信工程学院，山西 太原 030051）

0 引言

对弹体侵彻的研究可追溯到19世纪90年代，20世纪60年代美国进行的系列性航弹大地侵彻试验开始了真正意义上的侵彻试验研究［1］。在侵彻研究过程中，侵彻的目标逐步扩展到沙石、混凝土、铝靶、钢板等，并获得了大量的侵彻试验数据。美国Sandia国家实验室利用自行研制的小型侵彻过载加速度记录仪成功获取了弹丸侵彻混凝土目标的全弹道加速度测试曲线［2］。Forrestal等详细研究了弹丸侵彻混凝土目标的加速度测试方法，给出弹丸以不同速度侵彻不同强度目标的模型预测曲线和实弹测试曲线［3］。美国西北太平洋国家实验室的Booker等在研究片状混凝土目标对弹体的冲击响应过程中对实测数据进行了归零校正［4］。瑞士武器系统与弹药试验中心利用自行设计的高g值弹道飞行数据记录器FDR（flight data recorder），成功测得最大峰值90 000 g、脉宽200μs的侵彻加速度信号［5］。

国内，刘小虎等最早利用试验的方法获得了半球形头部钢弹垂直侵彻素混凝土目标的减加速度曲线［6］。景鹏等人则从测试的角度对弹丸侵彻硬目标的过程进行了试验研究，其研制的小型化弹载测试装置成功地获得了子弹侵彻不同目标的减加速度数据曲线［7－9］。

在上述已经公开报道的文献中，所有加速度曲线都被进行了处理，但具体的处理方法文中并未公开。为此，本文在对大量侵彻实测数据研究的基础上，提出了侵彻加速度信号零点漂移的修正原则和滤波截止频率的选择原则。

1 侵彻混凝土目标加速度信号的特征

射弹侵彻混凝土目标的过程是一个非常复杂的物理过程，通常分为开坑阶段和成孔阶段（即稳定侵彻阶段），开坑阶段由于弹体存在强烈的冲击振荡，加速度信号在时域曲线中表现为信号前沿存在高幅值的窄脉冲加速度。对于抗压强度较低的混凝土类目标，若弹体能够侵入或穿透目标，其成孔阶段的加速度信号表现为恒定值，如图1—图3所示，其中图3为瑞士武器系统与弹药试验中心报道的测试曲线；对于抗压强度较高的混凝土类目标，当弹体的侵彻速度不足以使其侵入目标内部时，在成孔阶段由于靶板表面的崩裂而没有形成稳定的侵彻过程，加速度信号在时域曲线中表现为信号呈现逐渐衰减的趋势，如图4—图5所示，其中图5为美国Sandia国家实验室报道的测试曲线。

图2 射弹垂直侵彻钢筋混凝土靶的加速度曲线Fig.2 Deceleration－time history for the reinforced concrete

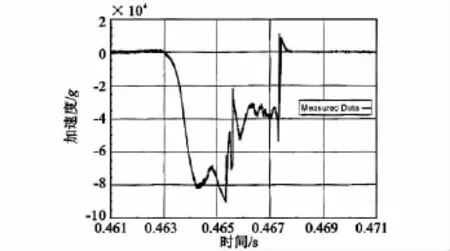
图3 瑞士的FDR记录的加速度曲线Fig.3 Axial acceleration data of FDR

图4 射弹垂直侵彻高强度素混凝土靶的加速度曲线Fig.4 Deceleration－time history for the concrete with high compressive strength

图5 Sandia国家实验室测得的轴向加速度曲线Fig.5 Axial acceleration data of Sandia’s recorder

通常，在撞击的瞬间会产生很强的应力波，弹体内各点的加速度实际上是应力波在弹体内传播的综合表现。在撞击初期，应力波将导致弹体各点加速度的第一个峰值；而在侵彻过程中的影响主要是对加速度曲线的振荡。因此，高g值加速度传感器的输出信号实际上包含了弹体的质心加速度、被测点相对于弹体质心的各阶振动加速度、安装结构相对于测试点的加速度响应以及加速度计对主激励信号的余响应。对于加速度传感器，由于其固有频率是有限的，通常很难真实响应弹体内由应力波所导致的第一个加速度峰值。应力波在撞击初期在弹体内的多个回合的往返，已导致弹体各点的加速度基本均匀，所以弹体的质心加速度可以认为是弹体各点加速度的平均值。

对图1、图2、图4的信号进行频谱分析，射弹侵彻混凝土目标的加速度信号的频谱主瓣宽度为2 kHz，也就是说，弹体的质心（刚体）加速度的频谱分量主要集中在2kHz以内，主瓣后的第一个频谱峰值对应于弹体的一阶振动（轴向振动），该频率分量主要取决于弹体的长度。

综上所述，对于混凝土类目标，侵彻加速度信号基本特征：时域曲线表现为单峰性，且微秒级的高幅值脉冲之后是毫秒级的低幅值持续加速度（小于50 000 g），弹体的刚体加速度频谱分量主要集中在2kHz以内，结构响应的频率分量主要集中在2～10 kHz。

2 侵彻加速度信号的处理原则

基于上述对侵彻混凝土目标加速度信号的特征分析，结合在侵彻混凝土目标测试中所获得的大量实测数据，以高g值加速度传感器在应用环境下的气体炮实验和Hopkinson杆冲击校准实验为基础，研究了侵彻加速度信号数据处理的相关原则。

2.1 零点漂移修正原则

原则1：依据冲击前后高g值加速度传感器输出零点的漂移量，对实测加速度信号从峰值点之后开始进行归零校正，然后根据传感器所获得的绝对速度对峰值点之后的加速度传感器灵敏度进行修正。

在侵彻测试数据的处理时经常发现，加速度信号在侵彻过程结束后没有回到其初始的零线，即存在“零漂”，导致加速度信号的一次积分和二次积分分别与侵彻速度和侵彻深度不一致。参考文献［10—11］研究了高冲击测量过程中所应考虑的具体问题，指出零漂是高冲击测量过程中普遍存在的现象，与压电传感器相比，压阻加速度传感器在其损坏或退变之前几乎不存在零漂。参考文献［12—13］详细研究了压电加速度传感器零漂产生的原因，包括传感器敏感元件的过应力、传感器各部件的物理错动、基座应变等，其中由于过应力引起的敏感元件晶畴改变是压电传感器零漂的主要原因，且多晶体的铁电陶瓷比单晶体的石英在高冲击下更容易产生零漂。

ISO 5347－10指出，当加速度信号中存在零漂时，可在冲击前的零点和冲击后的漂移零点之间画一条直线作为确定加速度量值的新的基线［14］。这种计算方法的前提是假设从加速度信号一开始就产生了零漂，且这种漂移是按线性规律变化的，显然这种假设与压电传感器的零漂机理是不一致的。参考文献［15］通过对压电加速度传感器的气体炮和Hopkinson杆校准实验研究，结合参考文献［16］对压电材料的本质分析，发现高g值加速度传感器的零漂发生在峰值加速度之后。根据实验结果，总结出关于加速度信号零点漂移的修正原则1。

2.2 滤波截止频率选择原则

原则2：在参照弹体结构响应的第一阶模态频率的基础上，结合实测加速度信号的第一频谱峰值，保证滤波前后加速度信号的积分速度不变或在一定的误差范围内。

在侵彻撞击的初始时刻，由于高幅值窄冲击脉冲的作用，弹体的高阶模态被激发，在加速度信号中表现为信号包含有较高的频率分量。而在研究侵彻弹体强度、侵彻引信和反侵彻防护时，更关心的是弹体的刚体加速度。要获得弹体的刚体加速度，必须对减加速度实测数据进行处理，而处理的关键是如何确定数字滤波器的截止频率。

对实测的侵彻减加速度信号进行频谱分析发现，信号的频谱分量存在许多频谱峰值点，理论上讲这些峰值点应该和弹体与轴向振动相关的模态频率相对应。但由于实弹侵彻过程对弹体的约束条件比有限元模拟施加的边界约束更复杂，所以实际的频谱峰值点与各阶模态频率有一定的偏差。

通过对大量实测数据的分析，以实测侵彻速度和侵彻深度作为比对标准，总结出了侵彻加速度信号滤波截止频率的选择原则2。根据原则2确定的滤波器截止频率通常称为临界截止频率，按此频率滤波得到的加速度称为弹体的刚体加速度。

3 实测加速度信号的数据处理

图6所示曲线为988型高g值压电加速度传感器测得的70mm射弹以556m／s的速度侵彻高强度（抗压强度48MPa）素混凝土圆筒靶的侵彻加速度曲线，包括膛内发射、自由飞行和撞击混凝土的全过程的加速度。自由飞行阶段的时间为179.2ms，飞行距离101.4m，弹丸平均速度为566m／s，而通断靶测得的平均速度为556m／s，两者相差1.8%，因此可以取代目前常用的通断靶。

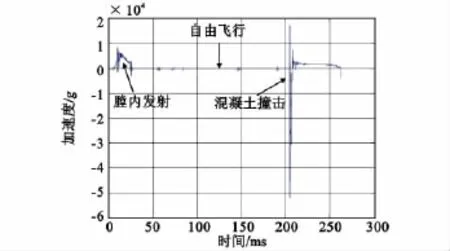
图6 弹体侵彻混凝土靶的全弹道加速度曲线Fig.6 Measured acceleration of projectile

图7为图6所示曲线混凝土撞击部分的展开图。从图中可以清楚地看出，加速度曲线在侵彻过程结束后存在一定的零点漂移。依据原则1对图7所示的曲线进行了修正，修正后的减加速度曲线如图8所示。

图7 混凝土侵彻减加速度曲线Fig.7 Measured deceleration－time history

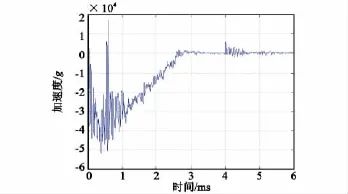
图8 侵彻减加速度修正曲线Fig.8 Corrected deceleration－time history

图9为图8所示减加速度曲线的频谱。从图中可以看出，加速度信号包含有较高的频率分量，频谱曲线在20kHz附近有谐振峰。

图9 减加速度数据频谱图Fig.9 Frequency spectrum of deceleration

为了获得弹体的模态频率，建立了测试弹（包括测试装置在内）的有限元模型，并取整个结构的进行分析。表1中第二行给出了分析结果，第三行给出了侵彻减加速度的频谱曲线中各阶峰值频谱数据。

从表1中可以看出，实测信号频谱峰值所对应的各阶频率都小于弹体的各阶模态频率，这主要是由于侵彻过程中混凝土靶对弹体施加的约束较强，从而降低了弹体的结构响应。信号的第1阶频率为3.2kHz，对应的振型为轴向振动，对轴向加速度信号影响较大。为了获得弹体的刚体加速度，可对测试信号以截止频率2.5kHz进行滤波，该频率为频谱曲线的主瓣宽度，见图9，滤波后的加速度曲线如图10所示。对测试信号以截止频率17kHz进行滤波后的曲线如图11所示，曲线含有一定的高频分量，其中主要是一阶模态振型（弹体的轴向振动）的影响，而二阶模态（弹体空腔部分的径向振动）及其以上振型对轴向加速度的影响很小。

经数值计算可知，对于数据处理过程中所选择的无相位失真滤波器filtfilt，其截止频率选择在2.5 kHz时不影响积分速度，当截止频率小于2.5kHz时，积分速度会随着截止频率的降低而减小。另外需要注意的是，对于不同的滤波器，在保证滤波前后加速度信号的积分速度不变的条件下，其所对应的截止频率是不同的。

综合以上分析，按照原则2，对图8所示加速度信号进行滤波可得到弹体的刚体加速度，加速度曲线经一次积分和二次积分得到的速度曲线和位移曲线如图12所示。积分速度为566m／s，积分位移为0.563m，与 实 测 得 到 侵 彻 深 度0.601m 相 差6.3%。

表1 弹体结构模态与频谱峰值对照表Tab.1 Comparison structural model of projectile and frequency spectrum of signal

图10 2.5kHz滤波后的加速度曲线Fig.10 Deceleration data filtered at 2.5 kHz with a digital low－pass filter

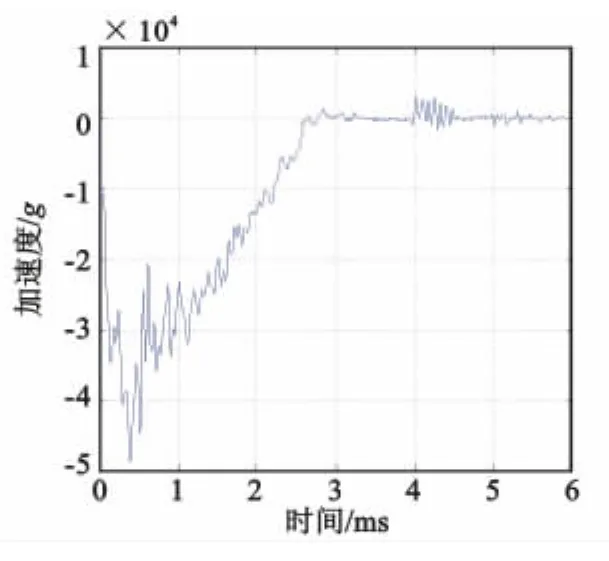
图11 17kHz滤波后的加速度曲线Fig.11 Deceleration data filtered at 17kHz

图12 积分速度和位移曲线Fig.12 Integral velocity and displacement data

4 结论

本文提出了针对存在“零漂”的侵彻加速度信号的数据处理的两条原则。零点漂移修正原则：依据冲击前后高g值加速度传感器输出零点的漂移量，对实测加速度信号从峰值点之后开始进行归零校正，然后根据传感器所获得的绝对速度对峰值点之后的加速度传感器的灵敏度进行修正。滤波截止频率选择原则：在参照弹体结构响应的第一阶模态频率的基础上，结合实测加速度信号的第一频谱峰值，保证滤波前后加速度信号的积分速度不变或在一定的误差范围内。数据处理结果表明：这两条原则对于实弹侵彻测试过程中获取的加速度信号是有效的，经处理后得到的刚体加速度完整地反映了弹丸侵彻混凝土目标过程中加速度的变化规律，弹体刚体加速度的一次积分与二次积分分别与实测的撞击速度和侵彻深度保持了较好的一致性，相对误差小于10%，能够满足侵彻测试的工程要求。

［1］Forrestal M J，Luk V K.Penetration into soil targets［J］.Int J Impact Eng，1992（12）：427－444.

［2］Franco R J，Platzbecker M R.Miniature penetrator（MIN－PEN）acceleration recorder development test［R］.USA：Sandia national laboratories，1998.

［3］Forrestal M J，Frew D J，Hickerson J P，et al.Penetration of concrete targets with deceleration－time［J］.Int J Impact Eng，2003（28）：479－497.

［4］Booker P M，Cargile J D，Kistler B L，et al.Investigation on the response of segmented concrete targets to projectile impacts［J］.International Journal of Impact Engineering，2009，36（7）：926－939.

［5］Rothacher T，Giger B.High g ballistic flight data recorder［C］／／18thinternational symposium on ballistic.San Antonio：IBS，1999：379－386.

［6］刘小虎，刘吉.弹丸低速垂直侵彻无钢筋混凝土的实验研究［J］.爆炸与冲击，1999，19（4）：323－329.LIU Xiaohu，LIU Ji.Experimental studies on the projectile penetrating normally into a plain concrete［J］.Explosion and Shock Wave，1999，19（4）：323－329.

［7］景鹏.高g值冲击测试关键技术研究［D］.太原：中北大学，2009.

［8］ZHANG W D，CHEN L J，XIONG J J，et al.Ultra－high g deceleration－time measurement for the penetration into steel target［J］.International Journal of Impact Engineering，2007（34）：436－447.

［9］FAN J B，ZU J，WANG Y，et al.Triaxial acceleration measurement for Oblique penetration of a rigid projectile into concrete target［C］／／Proceeding 25th IEEE Inter－national Conference Instrumentation and Measurement Technology.USA：IEEE，2008：196－199.

［10］Chu A.Problems in high－shock measurement［C］／／58th Shock and Vibration Symposium.USA：SAVIAC，1988.

［11］Patterson J D.Measurement considerations in pyroshock measurements ［C］／／Proceedings of the 44th International Instrumentation Symposium.USA：IEEE，1998：364－372.

［12］Chu A.Zeroshift of piezoelectric accelerometers in pyroshock measurement［C］／／Bulletin of the 57th Shock and Vibration.USA：SAVIAC，1987：71－80.

［13］Plumlee R.Zeroshift in piezoelectric accelerometers［R］.USA：Sandia Corporation Report，1971.

［14］ISO 5347－10－1993.Methods for the calibration of vibration and shock pick－ups：Part 10［S］／／Primary calibration by high impact shocks.Geneva，Switzerland：IX－ISO，1993.

［15］范锦彪.高g值加速度溯源性校准理论及高冲击测试技术研究［D］.太原：中北大学，2010.

［16］杨大智.智能材料与智能系统［M］.天津：天津大学出版社，2000.