基于几何光学近似模型的大气泡粒子散射光场分布计算

吕且妮 ，徐 畅 ，靳文华

(1. 天津大学精密仪器与光电子工程学院，天津300072；2. 天津大学光电信息技术教育部重点实验室，天津300072)

在基于粒子光散射理论的各种检测方法中，粒子散射光特性分析是其主要研究内容之一．散射光强计算常用的理论模型有 Mie理论[1-2]、Debye级数展开模型[3-4]、几何光学近似模型(geometrical optics approximation model，GOM)[2,4-13]．GOM 是基于光线理论计算每一束光线对散射场的贡献，并可以给出每一束光线的物理意义．在 GOM 模型中，由于散射角通常是入射角的多值函数，因此，利用 GOM 计算粒子散射光强分布，就必须求解出每个散射角所对应的入射角，也就是说，基于 GOM 模型的数值计算首先是要求解散射角所对应的所有入射角，这是基于GOM 理论计算散射光场分布必须首先要解决的问题．其方法之一是利用三角函数关系构建一个方程，求解该方程的解得到满足条件的入射角，如 Zhou等[11]利用cos(·)函数构造了散射角与入射角的多项式，采用牛顿迭代法和分段法相结合的方法求解多项式方程得到入射角，并开发了相对折射率大于1的大颗粒的 GOM 计算程序．文献[4]和文献[12]利用sin(·/2)函数构造了散射角与入射角的多项式，基于MATLAB语言编写了相对折射率小于1的大气泡的GOM 计算程序．吕且妮等[13]已经提出利用sin(·/2)和 MATLAB中的 fzero(·)函数的遍历取值的求解方法．本文分析了基于不同三角函数方程，利用MATLAB 中的 fsolve(·)函数/fzero(·)函数，采用遍历取值求解入射角的准确性和难度，给出了一种简便和准确的求解方法，计算了球形粒子的散射光强分布和散射相位分布，与 Mie理论计算进行了比对，并与文献[8]和文献[10]给出的计算结果进行了比较，结果吻合很好．

1 GOM理论模型

1.1 散射光强函数

图 1中，设波长为λ的平面平行光Ei入射于半径为a的球形粒子，散射光场分布包括反射光E0、折射光E1、E2、…、Ep( p=0,1,2,… ,为弦数)和衍射光?，其复振幅分布为

衍射光场Ediff的平行和垂直分量的复振幅分布分别为

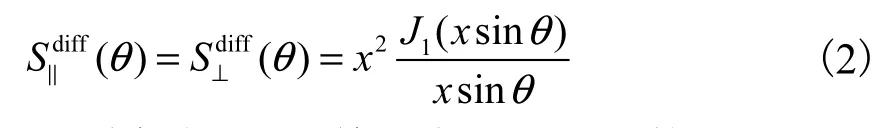
式中：θ为散射角；J1为第一类Bessel函数；x为粒子尺寸的无因次参数，

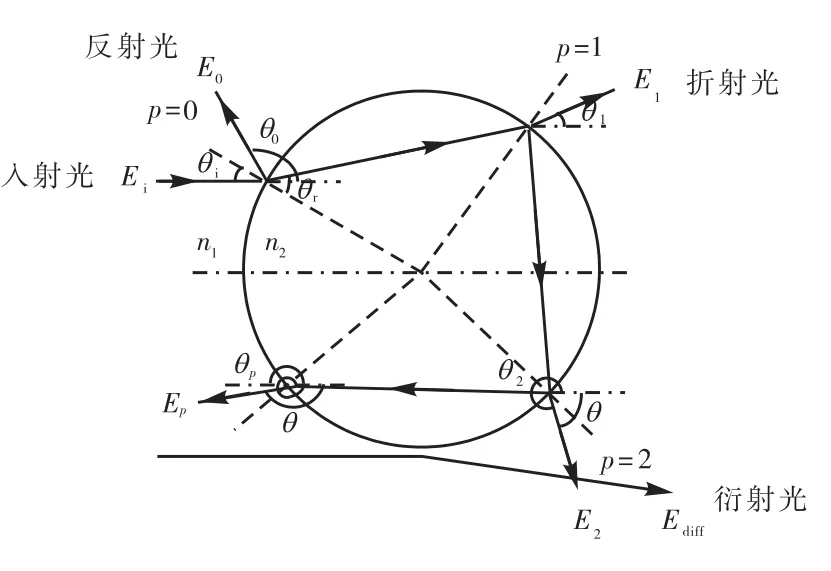
图1 GOM理论模型Fig.1 GOM theoretical model

反射光场E0和折射光场Ep的平行和垂直分量的复振幅[2]分别为

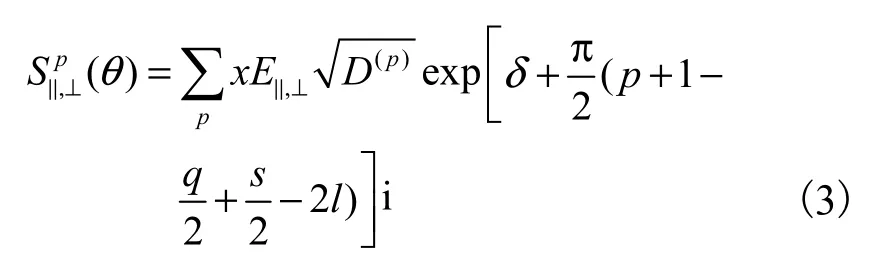
式中：p=0时为反射光，即E0；p=1时表示入射光折射进入粒子后再直接折射(透射)出粒子，即E1；p＞ 1表示入射光折射入粒子后，在粒子中发生(p−1)次反射，再折射(透射)出粒子．经粒子后的出射光Ep由入射角θi和弦数p唯一决定，其偏向角θp为

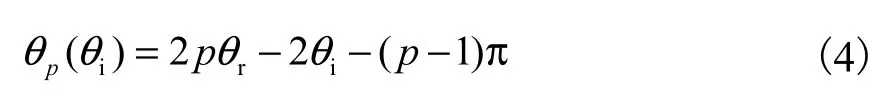
式中：s inθi=msinθr，θr为折射角，m=n2n1为粒子相对于介质的折射率；偏向角θp与散射角θ关系可表示为

式中q=±1，分别表示入射光从光轴的上半方和下半方入射．如图2所示，

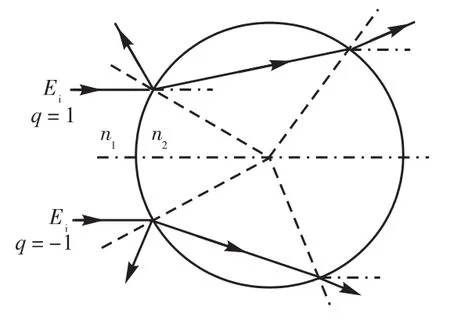
图2 q=±1时入射光的入射位置Fig.2 Incident ray position for q=±1

波前扩展因子为

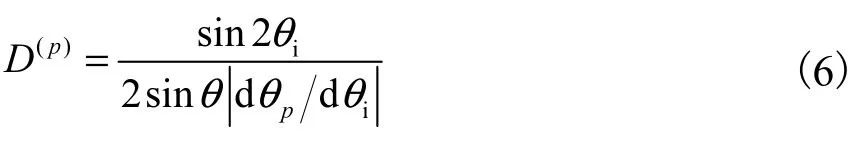
式中

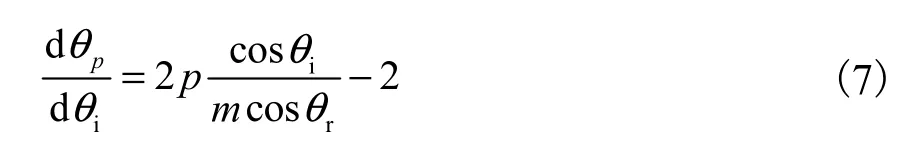
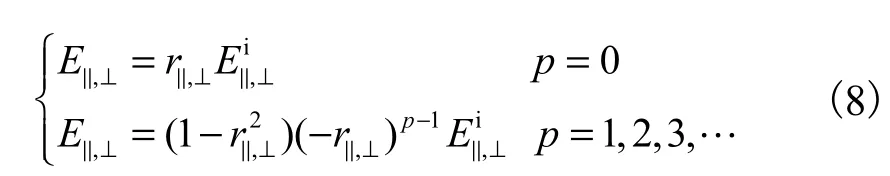
式中：Ei为入射光振幅；r⊥和r‖为费涅耳反射系数[14]，分别为

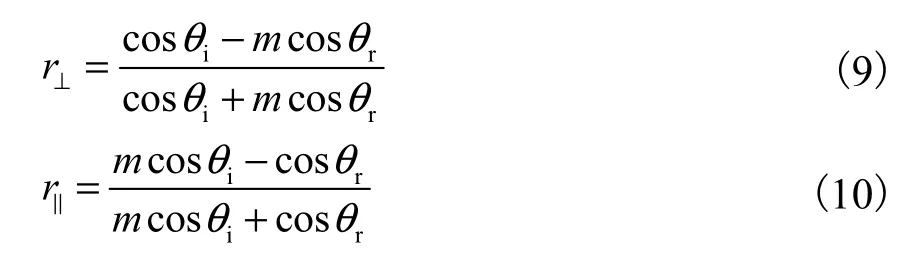
对m＜1，当入射角θi＞θC=arcsinm (临界角)时产生全反射，这时没有光入射到粒子内部．全反射引入的相位变化[14]为

E‖和 E⊥分别为

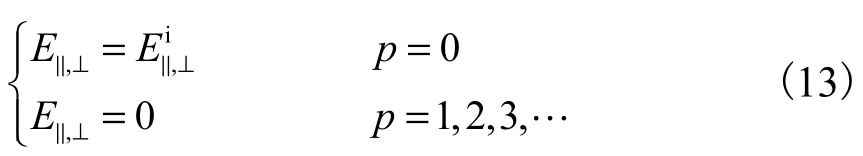
散射光场总的相位分布[8]为

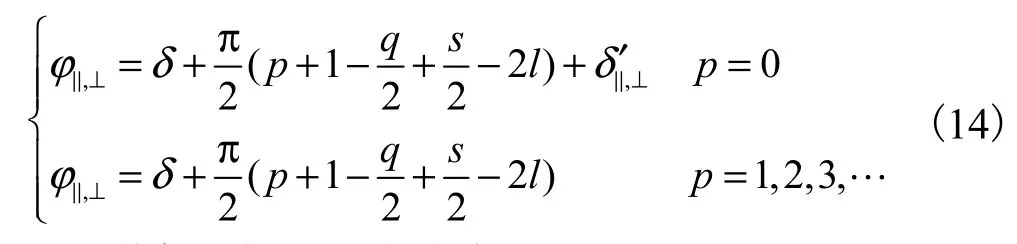
散射光场的强度分布

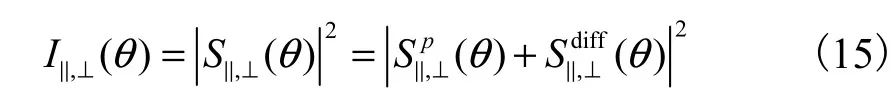
则非偏振光的散射光强分布为

1.2 散射相位函数

散射光能量分布的另一种描述是散射光的相位函数，它决定了光散射能量的角分布．非偏振光的散射光相位函数[9-11]为

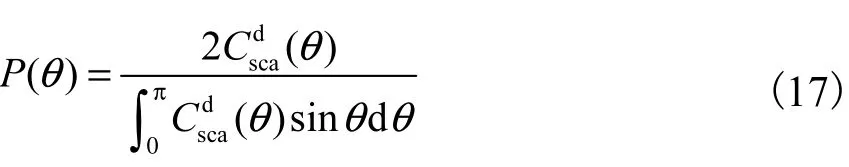
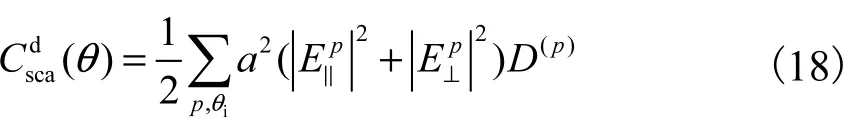
则其相位函数P()θ为

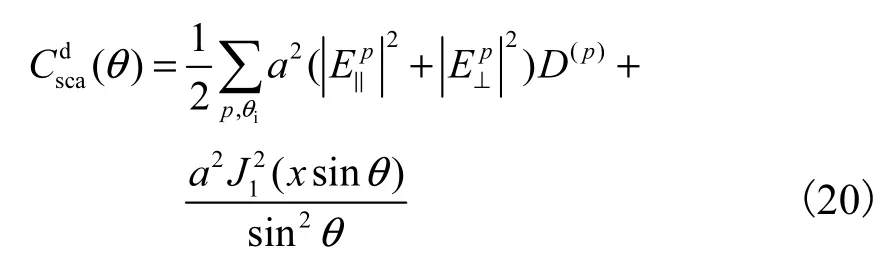
相位函数P()θ为

2 入射角-散射角的数值求解

由式(15)∼式(21)可知，散射光强I()θ和散射相位P()θ是散射角θ的函数，由式(4)和式(5)可知，散射角θ是入射角θi的函数，且是入射角θi的多值函数．对一散射角θ，其散射光强分布可能是由不同入射角的光线所共同作用的结果，因此，基于 GOM 模型的数值计算关键是已知弦数p和散射角θ，求满足式(4)和式(5)的所有入射角θi．分析式(4)可知，根据三角函数的特性，采用不同的函数将有不同形式的求解方法．

2.1 函数的构造

2.1.1 tan(θp/2)函数

根据正切函数特性，对式(4)有

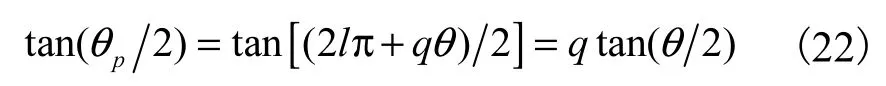
设

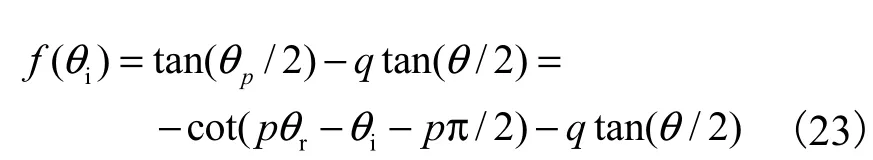
2.1.2 sin(θp/2)函数

根据正弦函数的特性，由式(4)得

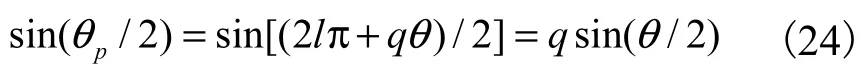
设

求解方程f(θi)=0的根，即可得到入射角θi．

2.1.3 sinpθ函数

对式(4)，不再对偏向角pθ取半角，直接采用周期为2π的sinpθ函数求解，即有

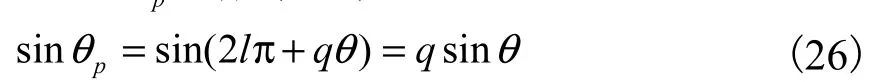
设

同样，求解方程 f(θi)=0的根，即可得到相应的入射角θi．

2.2 多项式方程的求解

构造多项式之后，将式(22)、(24)和(26)中的角度求解转化为求方程 f(θi)根的问题．本文采用MATLAB 中 fsolve(·)函数/fzero(·)函数求解方程其步骤为：对一给定的散射角θ和 p，设作为 fsolve(·)函数的求解估计值，其中Δθi为所设定的入射角取值间隔，n为正整数．对q=±1时，遍历所有估计值，返回求出的入射角θi，再将θ、p、q=±1以及求出的入射角θi代入式(5)，判断l是否为整数，若l为整数，保存入射角θi，否则说明给定的散射角θ无解．当遍历的较小时，通过 fsolve(·)函数可准确地求出每一个入射角θi．这种求解方法与文献[11]相比，不需要预判拐点．

2.3 结果及分析

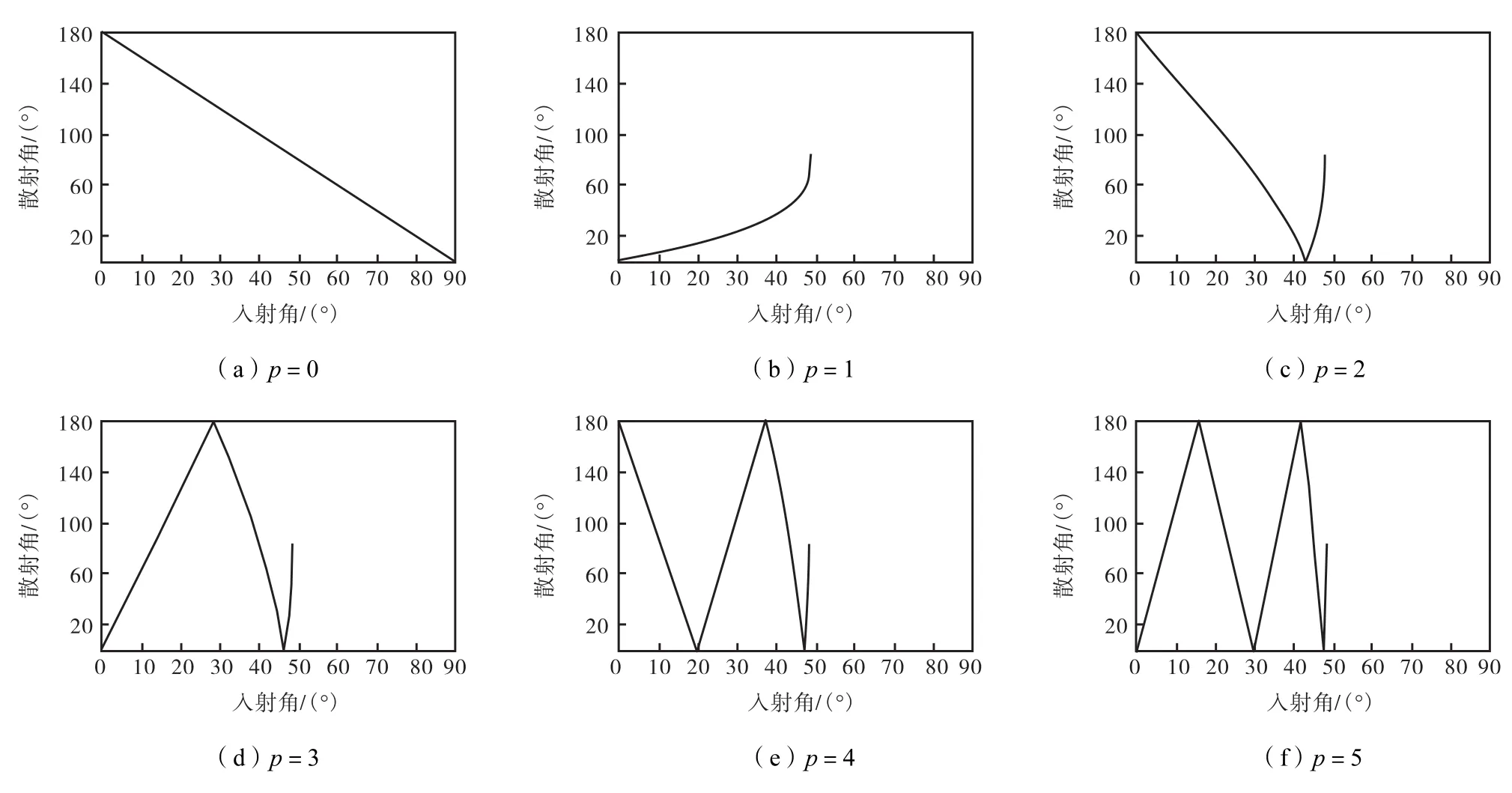
图3 m＝0.75时散射角与入射角关系Fig.3 Relationship between scattering angle and incidence angle for m = 0.75

分析式(24)可知，当l为偶数时，sin( 2)pθ=当l为奇数时，，因此，式(24)可表示为．由于则式(24)为．数学上，l的奇偶性并不影响式(24)，利用该函数同样可得到正确的入射角θi．对m＝0.75，其散射角所对应的入射角如图3所示，但所求出的入射角θi对应的q值将可能不正确．如对散射角θ=53°，求解得到的时，l=−1．此时，应取q=1，才能满足l为整数，进而得到正确的散射光强分布和散射相位分布．因此，在利用求解时，需要根据l的值，对q值进行修正．

对式(24)，l的奇偶性影响了 q的求解，但不影响入射角θi．为了避免l对q的求解影响，利用sinθp函数进行求解．图 4(a)为对m=0.75，利用该求解算法得到的 p＝4阶的入射角与散射角关系图．与图3(e)相比，在图4(a)中，一个入射角θi对应两个散射角θ′和这显然不对．对散射角θ′和π−θ′，由式(5)，则有

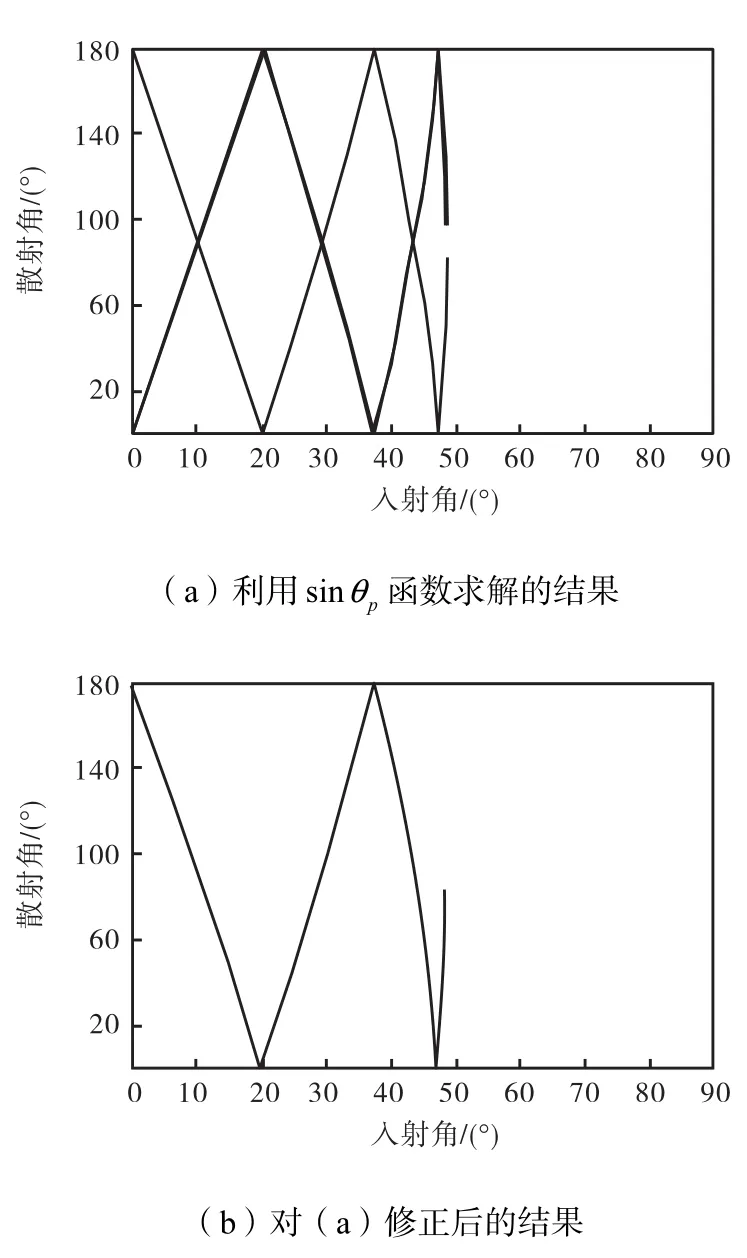
图4 m＝0.75、p＝4时散射角与入射角关系Fig.4 Relationship between scattering angle and incidence angle for m＝0.75,and p＝4

若设正确的散射角为θ′，则而将再不满足整数的限制条件，故散射角 π−θ′将不正确，应予以剔除．修正后的入射角与散射角关系如图 4(b)所示，与图 3(e)相同．

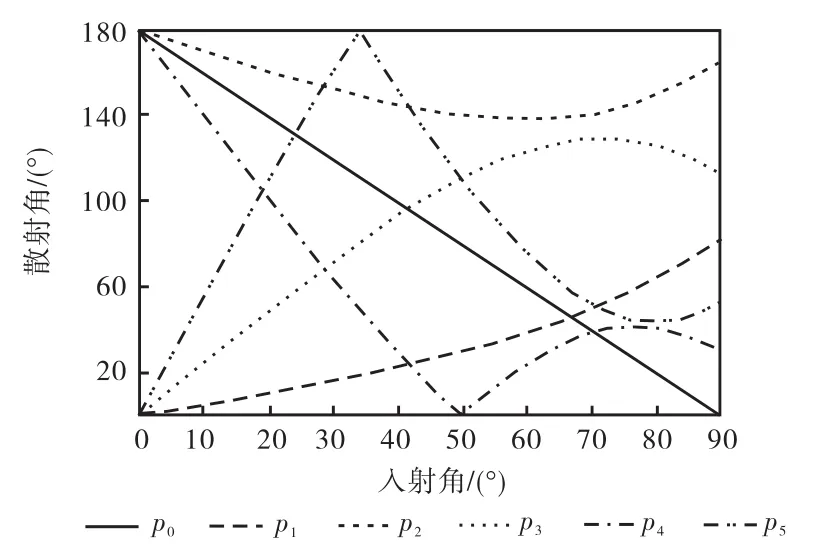
图5 m＝1.333时不同阶数p的散射角与入射角关系Fig.5 Relationship between scattering angle and incidence angle of various components p for m＝1.333

对上述 3种函数，采用 fzero(·)函数也可得到正确的θi和q值．文献[13]采用sin(θp2)函数和fzero(·)函数求解得到了相应的入射角．但对p≥4，散射角θ≈180°时，出现了入射角θi的缺值现象，主要原因是：fzero(·)函数是采用二分法或分割法等算法进行零点的求解，文献[13]在利用 fzero(·)函数计算时，将中间值作为估计值代入 fzero(·)函数进行求解，将区间值作为输入值即可．MATLAB中的fzero(·)函数和fsolve(·)函数都可求解给定初值附近的零值点，但fzero(·)函数的运算速度稍快，而 fsolve(·)函数可减小由估计值选择不当引起的缺值现象．

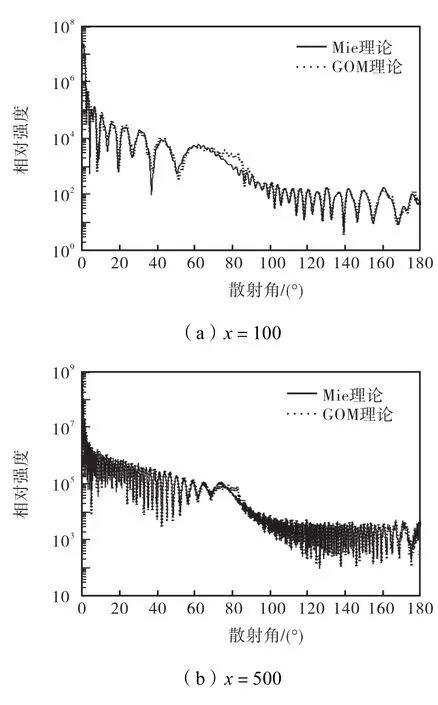
图6 m＝0.75时GOM和Mie理论计算的总散射光强比较Fig.6 Comparison of total scattering intensity calculated by GOM and Mie theories for m＝0.75

3 散射光场分布计算

利用上述的入射角-散射角求解方法以及式(15)～式(21)，分别计算了不同尺寸和不同折射率的球形粒子散射光强和散射相位函数分布．图6给出了m＝0.75、x取不同值时，基于 GOM 和 Mie理论计算的不同粒径的总散射光强分布，其中，截止阶数，基于GOM计算光强时，已计算了由全反射引入的相移量，图 6与文献[8]中的图 3完全吻合．图7为m＝1.333时，基于GOM和Mie理论计算的 x＝100、500的总散射光强分布，同样pmax=10.图6和图7中，随着粒子直径d的增大即x的增大，GOM 与 Mie计算的散射光强分布吻合越好．对图6，在θ=80°区域，GOM与Mie计算的散射光强分布有差异，是因为当θi=θC时，p=1阶的散射光剧烈减少，I→0．根据几何光学理论，当θ=π−2θC=82.82°时，没有光线进入到粒子内部产生高阶数的散射光，也就说散射角θ≤82.82°，即散射临界角θC=π−2θC=82.82°(可参看文献[13]中的图 6(b)).对图 7，在θ=130°区域，GOM 理论计算的光强分布出现了尖峰，该角度位置为光学彩虹角位置，此时扩散因子 D(p)(p, m,θi)→∞ ．图 8(a)所示为m＝0.75、m＝1.333时，基于 GOM 理论计算的球形粒子近场散射相位分布．由式(19)可知，近场散射相位分布与粒子尺寸和波长无关，图 8(a)与文献[10]中的图 2.7完全吻合．图 8(b)给出了m＝0.75和m＝1.333，基于 GOM 理论计算的不同粒径的球形粒子的远场相位图，其中截止阶数pmax=10．由图 8(b)可以看出，随着粒径的增大，散射相位函数分布趋于一致．这是因为当粒子尺寸不断增大时，夫琅和费衍射光场Ediff的贡献将逐渐减小，J1( x sinθ)→0．图 9(a)和图9(b)分别为波长λ＝0.55,µm，粒子半径a＝15,µm时，m＝0.75和m＝1.333的球形粒子远场相位分布，并与 Mie理论计算的非均匀粒子体系的散射相位分布进行了对比，其中对于 Mie理论，非均匀粒子分布服从半宽系数µ＝6的伽马分布、粒子有效半径a＝15,µm，图9与文献[10]中的图2.6相同．计算结果验证了该算法的正确性．

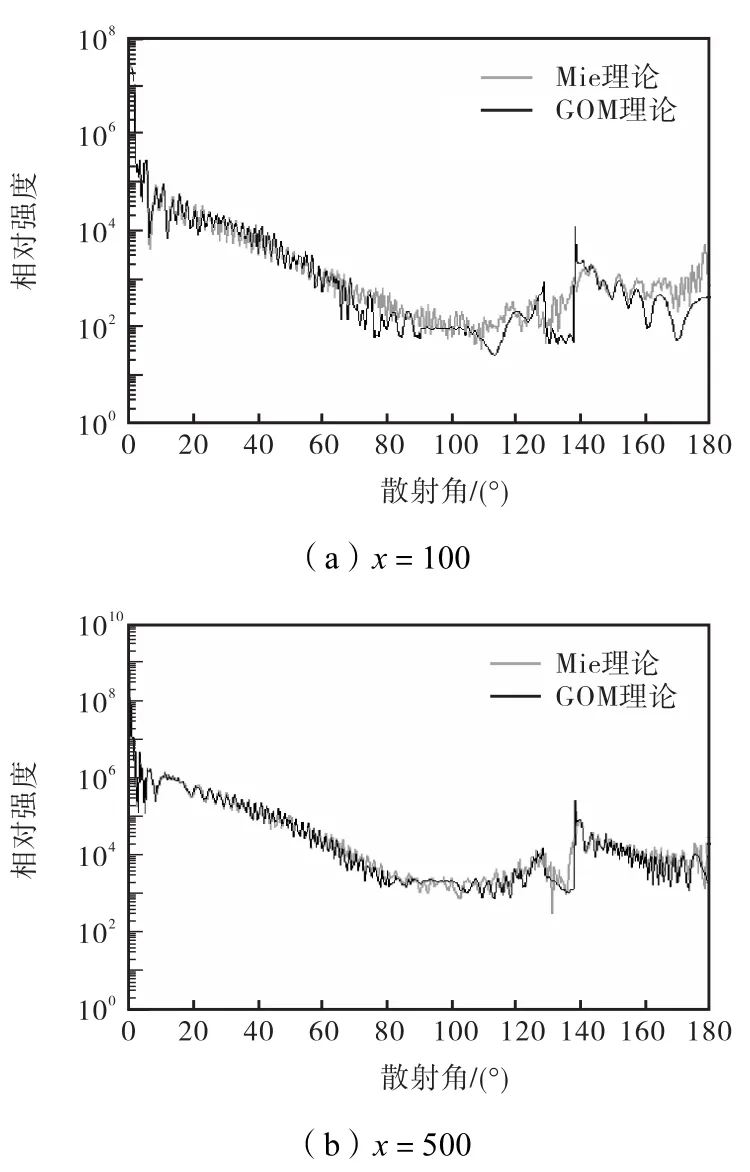
图7 m＝1.333时GOM和Mie理论计算的总散射光强比较Fig.7 Comparison of total scattering intensity computed by GOM and Mie theories for m＝1.333

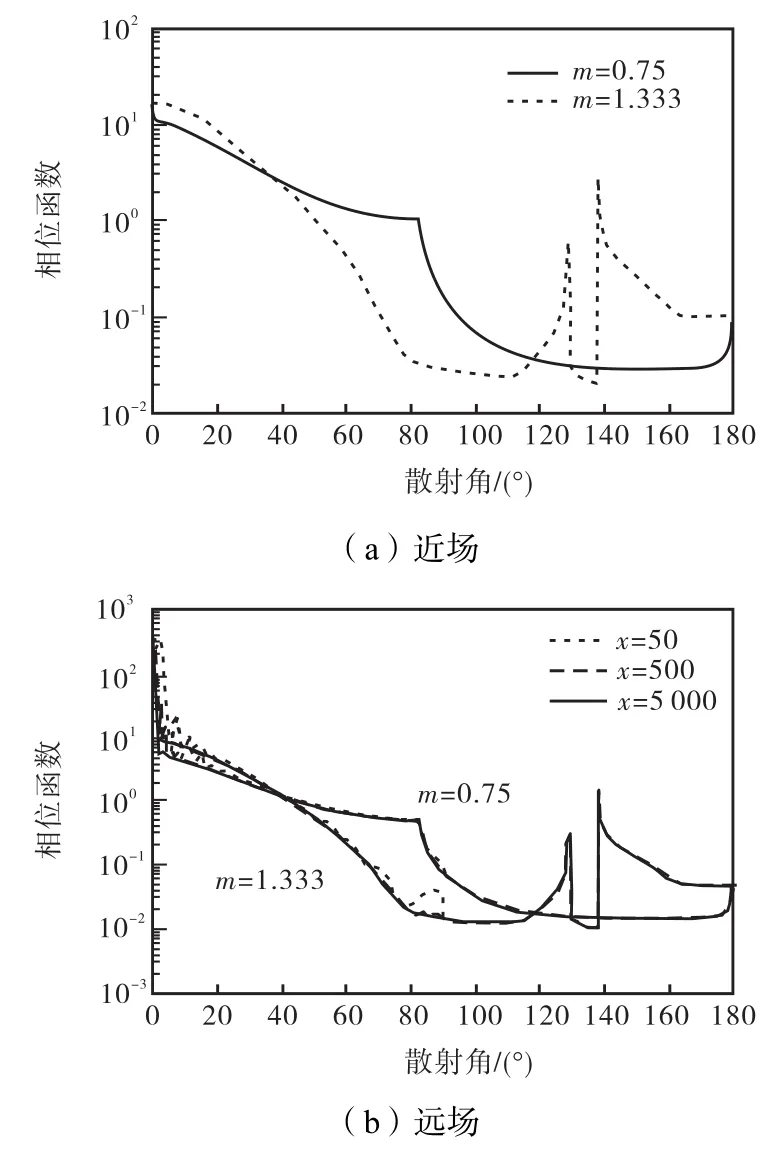
图8 GOM理论计算的相位函数分布Fig.8 Scattering phase function computed by GOM theory

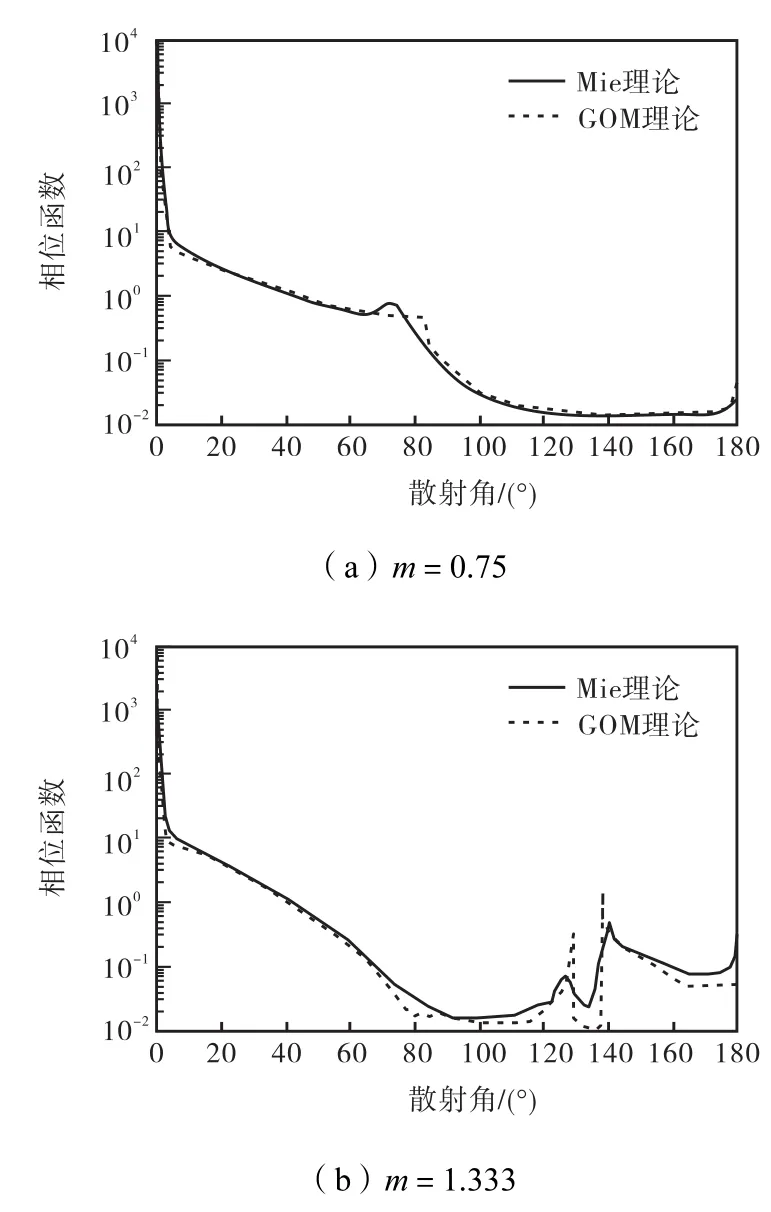
图9 GOM和Mie理论计算的散射相位函数分布Fig.9 Calculations of scattering phase function computed by GOM and Mie theories

4 结 语

本文对 GOM 基本理论进行了研究，并对 GOM中的入射角与散射角关系进行了分析，对比了不同三角函数的求解方法．sin(θp2)函数和sinθp函数两种方法均由于l的影响，使计算得到的 q值或入射角与散射角关系有所偏差．tan(θp/2)函数，由于其π的周期，无论l取何值时，式(22)将始终成立．相比前两种方法，无需加入任何约束条件以验证入射角θi和q值的求解是否正确，改善了程序的复杂度和运算量．利用本文所提出的多值散射角求解方法，计算了球形大气泡粒子和水粒子的总散射光强和散射相位分布，并与 Mie理论计算进行了比较，计算结果与 Mie理论计算结果吻合很好，验证了本算法的可行性和正确性.

［1］ Gogoi A，Choudhury A，Ahmed G A. Mie scattering computation of spherical particles with very large size parameters using an improved program with variable speed and accuracy[J].JMod Opt，2010，57(10)：2192-2202.

［2］ Van de Hulst H C.Light Scattering by Small Parti-cles[M]. New York：Wiley，1957.

［3］ Shen Jianqi，Wang Huarui. Calculation of Debye series expansion of light scattering [J].Appl Opt，2010，49(13)：2422-2428.

［4］ Wu L，Yang H R，Li X D，et al. Scattering by large bubbles：Comparisons between geometrical-optics theory and Debye series [J].J Quant Spectrosc Radiat Transf，2007，108(1)：54-64.

［5］ Xu F，Cai X S，Ren K F. Geometrical-optics approximation of forward scattering by coated particles [J].Appl Opt，2004，43(9)：1870-1879.

［6］ Li X Z，Han X E，Li R X，et al. Geometrical-optics approximation of forward scattering by gradient-index spheres [J].Appl Opt，2007，46(22)：5241-5247.

［7］ Li W，Yang K C，Xia M，et al. Computation of the scattering intensity distribution for natural light scattered by an air bubble in water [J].J Opt A：Pure Appl Opt，2006，8(1)：93-99.

［8］ Yu H T，Shen J Q，Wei Y H. Geometrical optics approximation of light scattering by large air bubble [J].Particuology，2008，6(5)：340-346.

［9］ Kokhanovsky A A. Optical properties of bubbles [J].J Opt A：Pure Appl Opt，2003，5(1)：47-52.

［10］ Kokhanovsky A A.Light Scattering Media Optics：Problems and Solutions[M]. Praxis，Chichester，UK：Springer，2004.

［11］ Zhou X B，Li S S，Stamnes K. Geometrical-optics code for computing the optical properties of large dielectric spheres [J].Appl Opt，2003，42(21)：4295-4306.

［12］ 李旭东，杨鸿儒，张 郁，等. 大气泡散射的几何物理模型数值计算[J]. 应用光学，2006，27(6)：539-542.Li Xudong，Yang Hongru，Zhang Yu，et al. Numerical calculation of light scattering caused by large spherical bubbles with geometrical-physical model[J].J Appl Opt，2006，27(6)：539-542(in Chinese).

［13］ 吕且妮，靳文华，葛宝臻，等. 粒子散射的几何光学模型中的多值散射角函数计算[J]. 光电子·激光，2010，21(11)：1677-1682.Lü Qieni，Jin Wenhua，Ge Baozhen，et al. Calculation of the multi-value scattering angle function in geometrical optics model for particle scattering[J].J Opt·Laser，2010，21(11)：1677-1682(in Chinese).

［14］ Born M，Wolf E. 光学原理[M]. 杨霞荪，译. 北京：电子工业出版社，2009.Born M，Wolf E.Principles of Optics[M]. Yang Xiasun，Trans. Beijing：Publishing House of Electronics Industry，2009(in Chinese).