电动汽车快速充电站需求分析与设备优化方法

刘文霞，仇国兵，张建华，杨 威

(1. 华北电力大学新能源电力系统国家重点实验室，北京 102206；2. 中国电力科学研究院，北京 100192)

电动汽车(electric vehicle，EV)充电系统的建设是电动汽车产业的重要支撑系统，也是电动汽车商业化、产业化过程中的重要环节．虽然目前电动汽车还处于示范运营阶段，但在其广泛的应用前景下，如何科学、合理地规划电动汽车充电站问题已经成为许多科技工作者关注的焦点．文献[1]重点分析了影响充电站规划的因素，提出了充电站规划中的技术原则；文献[2]针对居民电动汽车充电负荷进行预测，并以总费用为目标函数建立了充电站选址定容的最优费用模型；文献[3]提出了纯电动公交客车充电站电力负荷预测模型和计算方法，并分析了充电站配电容量的影响因素；文献[4]建立了电动汽车功率需求的统计模型，给出了电动汽车总体功率需求的计算方法；文献[5]提出了对混合型电动汽车和纯电动汽车充电站的优化设计，以尽量减少电动汽车充电时对电网造成的压力．以上文献针对不同种类的电动汽车进行了充电负荷预测，并建立充电站的个数和位置的优化规划模型，研究未涉及站内设备优化问题．

本文在对电动汽车种类、充电方式分析的基础上[6-9]，首先研究了电动汽车快速充电站的总量需求预测方法，分析了电动汽车快速充电站服务系统车辆达到状况和充电时间特性，建立了快速充电站的排队论数学模型，并利用愿望模型对充电站设备进行优化，得出充电机的最优配置数量，从而使得充电站的综合性能最佳，为合理规划电动汽车快速充电站提供了可靠的理论依据．

1 电动汽车快速充电站的需求分析

1.1 电动汽车充电方式

根据电动汽车动力电池组的技术和使用特性，电动汽车常用的充电方式[10]包括常规充电、快速充电和电池组快速更换．

不同种类的电动汽车根据自身的连续行驶能力和充电时间要求的不同，选择不同的充电方式．电动公交车可以利用夜间低谷时段进行常规充电，紧急时可选择快速充电或电池组快速更换；电动出租车在营运时段，可通过快速充电或电池组快速更换完成电能补给．

1.2 快速充电站的需求分析模型

电动汽车快速充电站的建站需求与某一地区的电动汽车快速充电电量的日需求总量有着密切关系．经分析可得电动汽车快速充电电量的日需求总量[11]为

式中：W∑为该地区电动汽车快速充电电量的日需求总量；i为电动汽车类型，包括电动小轿车、电动出租车、电动公交车等；βi为该地区i类型的电动汽车所需快速充电的比例；Ci为该地区i类型的电动汽车的保有量；Wi为i类型的电动汽车平均百公里耗电量；Li为i类型的电动汽车日平均行驶里程．

1.2.1 电动汽车保有量

根据相关资料分析，城市电动汽车保有量Ci与城市该类汽车保有量ki相关，而汽车的保有量与城市经济发展水平(GDP)、城市人口P及城市规模V等因素密切相关，一般采用多元回归分析方法，计算公式为

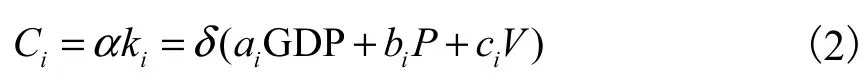
式中：ai、bi、ci为相关系数；δ为电动汽车渗透比例．

1.2.2 平均百公里耗电量

式中：kx为车辆行驶状况的修正系数；kr为道路状况的修正系数，视车道宽度、坡度大小及坡长而定(一般而言，单条车道越窄，道路纵坡越大，坡长越长，其值越大)；kq为气象修正系数，主要考虑雨雪、大雾、低温、高热等不良气象条件对耗电量的影响；kw为车辆荷载修正系数；wi为空驶条件下百公里耗电量．

1.2.3 日平均行驶里程

每车日平均行驶里程Li由电动汽车的使用特性和出行者的出行特性等因素共同决定，可以通过对电动汽车的行驶里程进行统计分析得出每车日平均行驶里程Li．

根据电动汽车快速充电电量的日需求总量和充电站日额定充电能力，推算出所需充电机数量，进而推算出所需充电站总量为

式中：N为充电站需求总量；Ni表示小、中、大型充电站的数量；WNi为各类快速充电站的日额定充电能力.

通过式(4)估算出充电站的基本数量，可以采用优化方法，结合地理和交通状况确定每个充电站的服务范围和服务车辆数，最后进行每个充电站的设备优化．

2 基于排队论的快速充电站的设备优化

2.1 快速充电站的排队模型

由于电动汽车到达充电站过程及其充电时间都是随机的，因此电动汽车快速充电站是一个典型的随机服务系统，故可利用排队论的方法对其进行优化设计．快速充电站的服务对象是各种不同类型的电动汽车，服务机构是充电机，称为服务台．对于一个电动汽车充电站来说，在某一时刻接受充电服务的电动汽车数量是有限的．电动汽车之间相互独立、随机到达，一般都希望到达后能在短时间内得到服务，但到达的电动汽车数量超过了充电站的容量时，顾客就必须排队等候．根据图 1所示，快速充电站排队系统可分为输入系统、输出系统、服务规则、排队模型、服务机构5部分，分析如下．

1) 输入系统

电动汽车到达快速充电站的过程是相互独立的，满足下述特点：在某一段时间内，电动汽车到达充电站的数量n的概率与这段时间的起始时刻无关，只与这段时间间隔的长短有关；在不相交的时间间隔内到达充电站的电动汽车数量是相互独立的；在充分小的时间Δt内同时到达 2辆及以上电动汽车的情况不存在或概率非常小，即满足平稳性、无后效性及普通性的特点．因此，可以用泊松流来表示电动汽车到达充电站的规律[12]，从而可得电动汽车到达快速充电站的时间间隔服从负指数分布．

2) 输出系统

每辆电动汽车到达充电站时电池所剩的载荷量是不同的，故不同电动汽车所需的充电时间是相异的且无记忆性，即先前电动汽车的充电时间对后来的电动汽车所需的充电时间无影响．因此，可用负指数分布来描述充电时间[12]．

3) 服务规则

每个充电机只能为一辆电动汽车充电，充电机无空闲时，后到达的车辆需排队等候，哪个充电机有空就到哪个充电机进行充电．

4) 排队模型

充电站的排队采用单通道、等待制、先到先服务的规则．

5) 服务机构

充电站对多台电动汽车同时进行服务，属于多服务台，且每辆电动汽车的充电时间相互独立．

由上述分析可以确定电动汽车快速充电站的排队模型是一个标准的M/M/s(输入过程为泊松输入/服务时间服从负指数分布/s个服务台)模型．

图1 排队系统结构示意Fig.1 Structure scheme of queuing system

为了问题的描述，定义以下符号：s为服务台数量，即可为s辆电动汽车同时充电；λ为顾客到达率，即电动汽车到达充电站的平均到达率，辆/h；μ为平均服务率，即平均服务能力，辆/h．

电动汽车快速充电站排队系统特征的基本参数是系统的状态，设充电站在时刻t有n辆电动汽车，称系统的状态为n，同时，记充电站在时刻t状态为n的概率为Pn(t)，它决定了电动汽车充电站排队系统的运行特征．当系统运行一定时间达到平稳状态后，对任一个状态n来说，单位时间内进入该状态的平均次数和单位时间内离开该状态的平均次数应相等，即系统在统计平衡下“流入＝流出”．

据此，可得电动汽车快速充电站排队系统任一状态下的平衡方程[13]为

在含有s个充电机的快速充电站服务系统中，当0≤n≤s时，系统中有n辆电动汽车正在接受充电服务，其余s-n个充电机处于空闲状态，此时系统平均服务率μn为nμ；当n＞s时，系统中s个充电机都在进行充电服务，其余n-s辆电动汽车排队等候充电，此时系统平均服务率μn为sμ．系统在任意时刻的电动汽车平均到达率都相等，即λn＝λ．故有下式成立，即

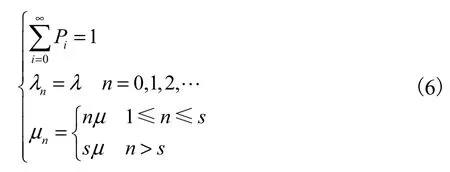
由式(5)和式(6)可得

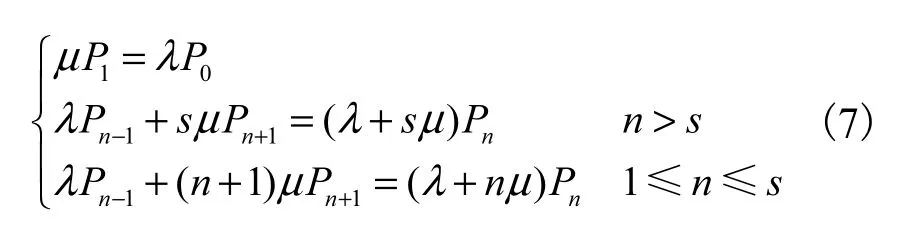
用递推法求解上述差分方程，可求得状态概率

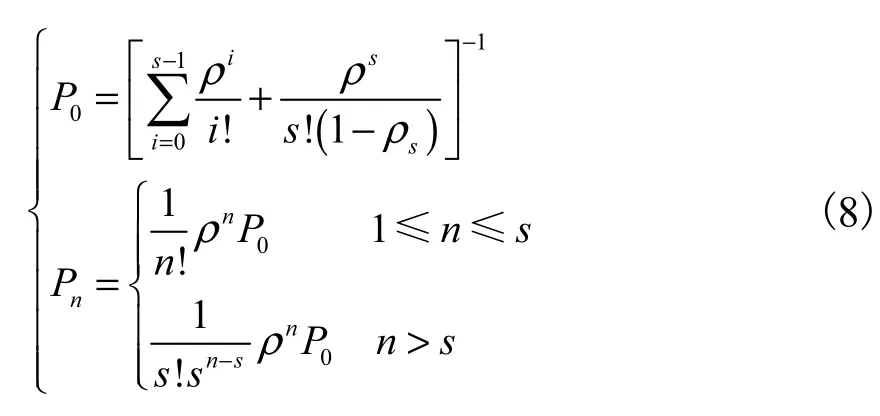
式中：ρ和sρ分别代表单服务台的服务强度和多服务台的服务强度且充电站排队系统只有在sρ≤1时，才不会排成无限长的队列，系统才能稳定运行．

由式(8)可求得系统空闲概率和系统中有n辆电动汽车的概率，它们都是服务台数 s的函数．在充电站设备优化中，已知参数λ和 μ，如何确定最佳的 s，这就涉及到如何确定系统目标的问题．

2.2 电动汽车快速充电站的设备优化

在电动汽车快速充电站排队系统中，顾客方总希望能够快速接受充电服务，在充电站逗留的时间越短越好，因而充电机数量越多越好，这样顾客花费时间少，遭受的损失就小．从充电站一方考虑，当充电机台数增加时就会增加投资，并且当充电站空闲还会造成设备浪费．因此，对任何一个排队系统的设计与运营管理，就需要考虑顾客与服务双方的利益，以便在某种合理指标上使系统达到最优．

通常，排队系统的优化问题常用费用模型进行求解，而在实际问题中，如何估算等待费用缺乏必要的数据和材料，不可能对顾客的等待时间用固定的货币值进行度量，例如不同年龄段的人同样等待一个小时所产生的损失费用是不同的，同一个人在不同时间的等待损失费用也是不同的，利用费用模型进行优化是不合适的．因此，笔者采用愿望模型，即直接利用系统的运行特征来确定设计参数的最优值．具体是：决策者根据愿望确定相互冲突的两个系统指标的上限，这些量是决策者希望均衡的量[14]，在同时满足两个冲突量限制的条件下，确定系统服务台数的最佳值．

快速充电站排队系统有以下5个性能指标．

(1) 平均排队等待的队长Lq，即系统中排队等待充电的电动汽车数量的期望值

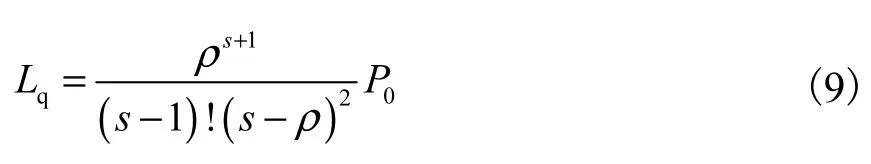
(2) 平均队长Ls，即系统中电动汽车数量的期望值

(3) 平均等待时间Wq，即电动汽车在系统中排队等待时间的期望值

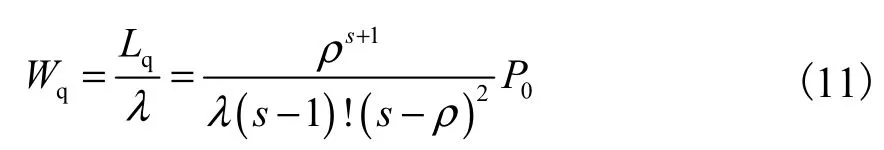
(4) 平均逗留时间Ws，即电动汽车在系统中停留时间的期望值

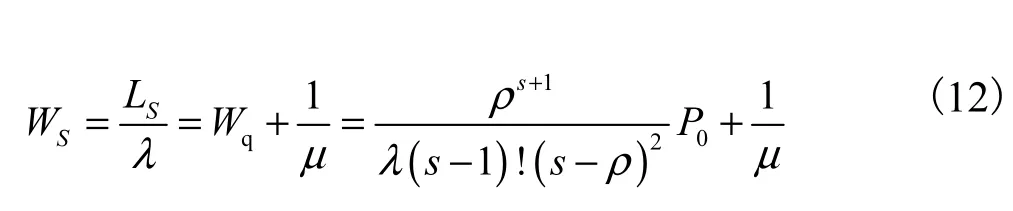
(5) 充电机空闲比例I，即充电机空闲比例的期望值

在上述系统指标中，Lq、Ls、Wq、Ws随着s增大而减小，即顾客损失减小；I随着s的增大而增大，即设备空闲率增大．因此选择顾客在系统中的平均逗留时间Ws和充电机空闲时间的比例I互为矛盾的两项指标的上限作为愿望条件，以此确定最佳服务台数s．决策者可以分别确定其意向的水平α和β，作为上述两项指标的上界值．满足式(14)的s值即被看作是最佳的服务台数．

愿望模型的求解方法可用图 2来表示．从图中可以确定s的取值范围．若α和β的值定得过低时，有可能发生无可行解的情况，这时可以分别或同时提高α和β的值．通过上述方法可以确定电动汽车快速充电站充电机的最优个数．

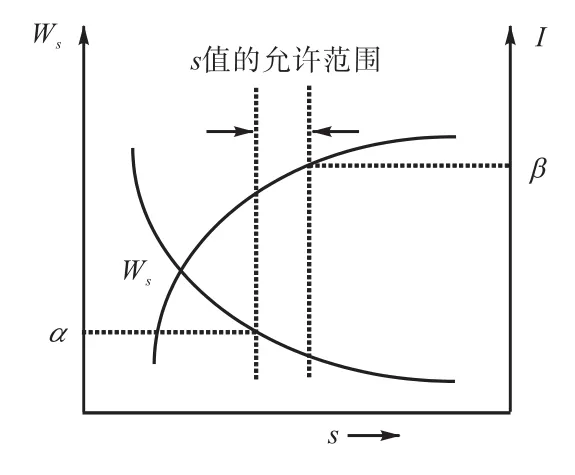
图2 愿望模型示意Fig.2 Schematic diagram of desire model

3 快速充电站规划设计总体流程

根据地区电动汽车规划，按照图3所示的流程进行快速充电站的需求分析和设备优化设计．

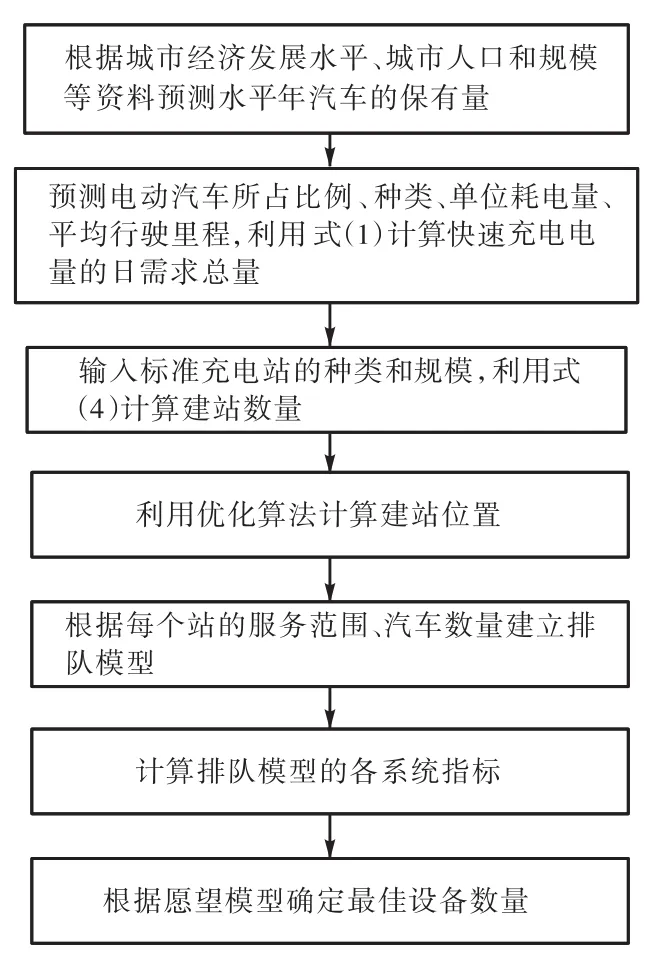
图3 电动汽车快速充电站设计总体流程Fig.3 Overall flow of EV fast charging station design

4 算例分析

4.1 实例计算

目前，各地电动汽车发展规划和充电站标准正在制定中，电动汽车的数量还比较少．本文以某试点地区为例进行快速充电站的设备优化．该地区一天内有 1,500辆电动汽车需进行充电，其中需要快速充电的有 150辆，充电站的服务时间为 6：00—23：00，利用最大似然法估计可得车辆平均到达充电站服从λ＝8.333辆/h的Possion分布．由于每辆电动汽车到达充电站时电池所剩的载荷量不同，所需的充电时间也各不相同，此处取30,min为电动汽车的平均充电时间，由最大似然法可得电动汽车的充电时间服从μ＝2辆/h的负指数分布．由ρs≤1可得s需满足s≥5的条件才能满足系统稳定运行，故可取 5≤s≤12．将已知的有关数据输入到MATLAB程序[15]中运算，则可得相关数据如表1所示．

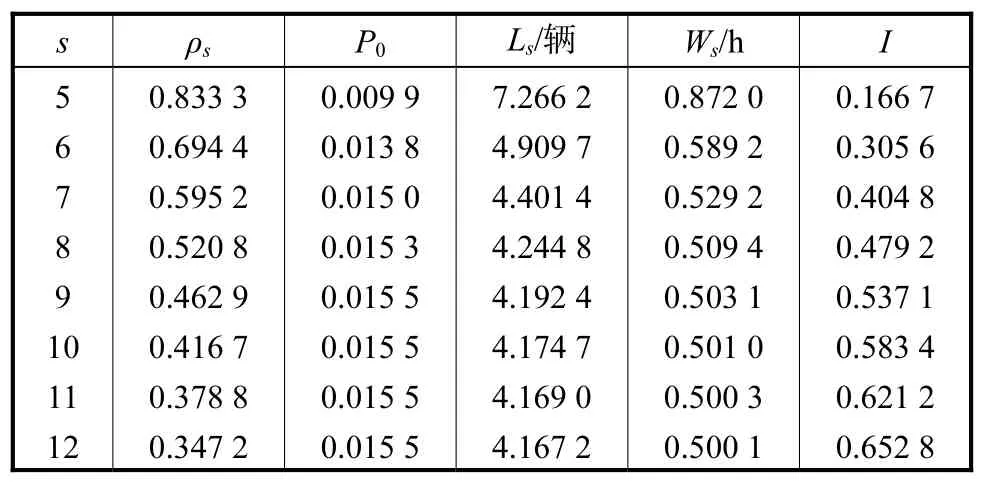
表1 电动汽车快速充电站设备优化指标计算Tab.1 Indexes’ calculation of EV fast charging station optimization

由表 1分析可得，当s值较小时，顾客的平均逗留时间Ws和充电站空闲率P0受s的影响较大．如当s＝5时，此时 Ws为 0.872,0,h；而当 s＝6时，Ws减小为 0.589,2,h，减小了 32.43%；当 s值增大时，顾客的平均逗留时间 Ws和充电站空闲率 P0受 s的影响减小，甚至可以忽略不计．如当 s＝8时，Ws为0.509,4,h；而当 s＝9时，Ws仅减小为 0.503,1,h，减小了 1.23%．而随着 s的增加，充电机的空闲比例 I逐渐增大．

综上可得，随着充电机台数 s的增加，系统服务强度随之减小，充电机空闲率逐步增大，系统相应平均队长减小，顾客平均逗留时间减小，系统的服务率提高．当充电机台数 s较小时，s的变化对 P0、Ws的影响较大．当 s增加到一定程度时，增加充电机台数s对 P0、Ws的影响较小，甚至可以忽略不计，对改善系统营运效果不佳．此时，增加充电机的数量不仅增加充电站的设备投资，而且会造成空闲时设备的极度浪费．

4.2 优化分析

笔者利用愿望模型对电动汽车快速充电站排队系统进行优化，故需首先确定两项指标的上限值，即Ws≤α和I≤β式中α和β的值．

当代世界人们越来越珍惜时间，据行为科学家研究发现：通常状态下，一个人在等候超过 10,min，情绪开始急躁；超过 20,min，情绪表现厌烦；超过40,min，常因恼火而离去．考虑到电动汽车充电时间的特殊性，可取α＝0.6,h．

随着充电机台数的增多，顾客的逗留时间必然减少．然而，同样会造成设备的空闲率过高，造成设备的资源浪费，显然配置过多的充电机不合理，故需控制设备的空闲率．考虑到在忙时充电机的空闲率会剧减，在此取β＝0.5．

由上述假定可得

由表1可得，当n＞8时，Ws和P0随s的变化均不大，即充电机台数在 n＞8时对平均逗留时间及充电站空闲比例的影响可以忽略不计．因而，s的值可取 s＝6，7，8，且均满足式(15)的要求．考虑到上述计算是利用平均到达率λ＝8.333辆/h进行求解的，在车辆高峰时取s＝6或7可能会造成队列过长或逗留时间过长的情况，因而取最大值 s＝8，即在该电动汽车充电站配置8台充电机可使系统达到最优．

5 结 语

本文在对电动汽车快速充电站进行需求分析的基础上，提出了规划和设计的总体流程，给出了需求计算模型．在分析车辆到达及充电时间规律的基础上，将排队论知识应用到充电站服务系统中，建立相应的数学模型．最后，利用愿望模型对充电站服务系统进行设备优化，分析得出充电机的最优配置数量，为合理规划电动汽车快速充电站提供了决策依据．但值得注意的是，本文在求解平均到达率和平均服务能力时进行了假设，具体应用该模型求解时应根据实际统计的充电站数据进行求解；利用愿望模型求解时，可以根据实际规划情况设定平均逗留时间和服务台空闲率的上限值．

［1］ De Forest N，Funk J，Lorimer A. Impact of Widespread Electric Vehicle Adoption on the Electrical Utility Busi-ness：Threats and Opportunities [EB/OL]. http：// cet.berkeley. edu/dl/Utilities_Final_8-31-09. pdf，2009-08-31.

［2］ 寇凌峰，刘自发，周 欢. 区域电动汽车充电站规划的模型与算法[J]. 现代电力，2010，27(4)：44-48.Kou Lingfeng，Liu Zifa，Zhou Huan. Modeling algorithm of charging station planning for regional electric vehicle[J].Modern Electric Power，2010，27(4)：44-48(in Chinese).

［3］ 王震坡，孙逢春，林 程. 电动公交客车充电站容量需求预测与仿真[J]. 北京理工大学学报，2006，26(12)：1061-1064.Wang Zhenpo，Sun Fengchun，Lin Cheng. Forecasting and simulation of the distribution capacity of E-bus charge station[J].Transactions of Beijing Institute of Technology，2006，26(12)：1061-1064(in Chinese).

［4］ 田立亭，史双龙，贾 卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术，2010，34(11)：126-130.Tian Liting，Shi Shuanglong，Jia Zhuo. A statistical model for charging power demand of electric vehicles[J].Power System Technology，2010，34(11)：126-130(in Chinese).

［5］ Bai Sanzhong，Du Yu，Lukic S. Optimum design of an EV/PHEV charging station with DC bus and storage system[C]//Proceedings of Energy Conversion Congress and Exposition．Atlanta，US，2010：1178-1184.

［6］ Acha S，Green T C，Shah N. Impacts of plug-in hybrid vehicles and combined heat and power technologies on electric and gas distribution network losses [C]//Proceedings of the IEEE PES/IAS Conference on Sustainable Alternative Energy．Valencia，Spain，2009：1-7.

［7］ Ford A. The impacts of large scale use of electric vehicles in southern California[J].Energy and Buildings，1995，22(3)：207-218.

［8］ Shrestha G B，Chew B C. Study on the optimization of charge-discharge cycle of electric vehicle batteries in the context of Singapore[C]//Proceedings of Australasian Universities Power Engineering Conference. Perth，Australia，2007：1-7.

［9］ Qian Kejun，Zhou Chengke，Allan M，et al. Load model for prediction of electric vehicle charging demand[C]//Proceedings of the International Conference on Power System Technology. Hangzhou，China，2010：1-6.

［10］ 康继光，卫振林，程丹明，等. 电动汽车充电模式与充电站建设研究[J]. 电力需求侧管理，2009，11(5)：64-66.Kang Jiguang，Wei Zhenlin，Cheng Danming，et al.Research on electric vehicle charging mode and charging stations construction [J].Power Demand Side Management，2009，11(5)：64-66(in Chinese).

［11］ 卢志成，黄 云. 城市机动车加油站需求预测与规划布局方法探讨[J]. 规划师，2011，27(2)：99-103.Lu Zhicheng，Huang Yun. City gas station needs prediction and planning layout method [J].Planners，2011，27(2)：99-103(in Chinese).

［12］ 姚红云，韩 玲，付玉元. 基于排队论的高峰期汽车加油站优化研究[J]. 交通信息与安全，2010，28(5)：28-30.Yao Hongyun，Han Ling，Fu Yuyuan. Gas station optimization in rush hours based on queuing theory [J].Journal of Transport Information and Safety，2010，28(5)：28-30(in Chinese).

［13］ 徐玖平，胡知能. 运筹学 [M]. 北京：科学出版社，2003.Xu Jiuping，Hu Zhineng.Operations Research[M].Beijing：Science Press，2003(in Chinese).

［14］ 赵可培. 运筹学[M]. 上海：上海财经大学出版社，2008.Zhao Kepei.Operations Research[M]. Shanghai：Shanghai University of Finance & Economics Press，2008(in Chinese).

［15］ 黄大明，文 冰，蒋顺梅. 基于排队论的港口运输装卸服务系统优化方法研究[J]. 广西大学学报：自然科学版，2009，34(6)：780-786.Huang Daming，Wen Bing，Jiang Shunmei. An optimized method for the loading/unloading system of port transportation based on queuing theory[J].Journal of Guangxi University：Natural Science Edition，2009，34(6)：780-786(in Chinese).