应用改进遗传规划方法的快堆功率控制策略

方 涛，陆道纲，段天英

(1. 华北电力大学核科学与工程学院，北京102206；2. 中国原子能科学研究院中国实验快堆工程部，北京102413)

快中子增殖反应堆由于其自身的一些特点，其控制方式和特点与热中子反应堆不尽相同，主要表现在：①堆芯富集度高、能谱硬，造成多普勒效应比热堆小，再加上缓发中子份额小，中子代时间短，要求控制器具有更快的响应速度；②采用金属钠作为冷却剂，没有可溶毒物反应性控制，采用了单一的控制棒控制方式，这就要求系统具有更高的控制精度；③堆芯紧凑、功率分布均匀，这有利于控制；④热中子极少，裂变产物氙和钐不再重要，可无需考虑毒物效应[1]．

通过以上比较不难发现，快堆功率控制要求有更高的响应速度和控制精度，且不易实现．在对快堆功率进行控制时，反应堆功率的变化会引起燃料温度的变化，从而导致反应性的变化，这反过来又会对功率的变化产生影响．造成这种反应性温度反馈的因素有很多，其中主要包括多普勒效应、燃料膨胀效应、冷却剂温度反应性效应、堆芯径向膨胀反应性效应以及堆芯弯曲反应性效应和控制棒轴向伸长等．反应堆功率由裂变功率和衰变功率两部分组成．裂变功率在裂变时立即产生，大小由中子通量和裂变截面决定；而衰变功率是由裂变后不稳定的裂变碎片与中子俘获产物再次衰变产生，其大小与裂变功率、燃料的同位素构成以及反应堆的运行历史都有关．瞬发功率可近似看成是中子通量的线性函数；而衰变功率在时间上有延迟，有可能会造成功率控制上的过冲现象，即如果仅通过控制裂变功率达到指定功率水平后，由于衰变功率的影响，功率继续升高，超过功率的期望值，这时要反方向移动控制棒来抵消衰变功率的影响．于是在控制上必须考虑这种影响，提前预测功率(或反应性)的变化，通过改善控制棒提升或下插的速度及大小，来防止该现象的发生[2]．

因此，快堆功率控制的难点就在于找到一个合适的功率(或反应性)预测模型以及如何防止功率控制上的过冲现象(这两者也是相互关联的)．目前，国外已有部分学者尝试采用模糊控制、人工神经网络等智能控制方法加以解决，并取得了一定成果[3-5]．但这些尝试大多都过于复杂，且没有考虑功率控制上的过冲现象．笔者针对这些问题采用了一种把改进后的遗传规划方法与反应堆动态周期方程相结合的方式，对中国实验快堆的数据样本集进行了仿真，并验证了模型的精度与预测结果．

1 反应堆动态周期方程

1.1 反应堆动态周期方程及约束条件

所谓反应堆周期，是指中子密度按指数规律变化e倍所需的时间，其符号和大小直接反映了堆内中子增减变化的速率．反应堆动态周期方程是一个随时间变化的函数，反映了各个时刻上堆内中子的变化情况[6]．

麻省理工大学的 Bernard[7]曾利用单群的点堆动态方程(由于快堆堆芯紧凑，且功率分布均匀，单群方程完全满足)，推导出一个反应堆动态周期τ与反应性、反应性变化率以及缓发中子先驱核分布相关的随时间变化的方程

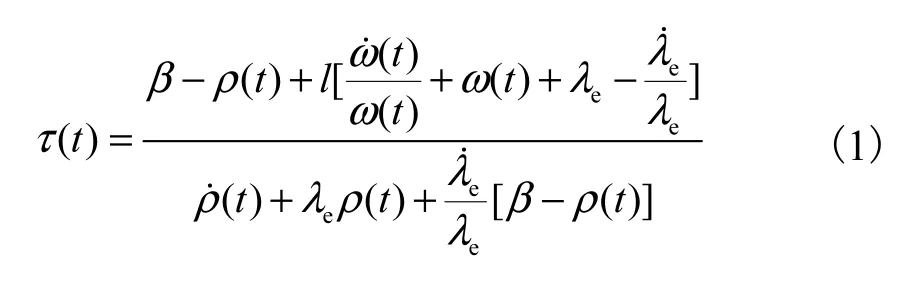
式中：β为有效缓发中子份额；ρ为反应性；l为中子代时间；ρ˙表示反应性的变化率；ω(t)为相位函数；，λ为先驱核的衰变常数，C为先驱核浓度．

由于瞬发中子寿命极短，而快中子更加明显，亦即l极小，因此式(1)可近似为

根据反应堆动态周期方程，又可分别推导出反应性的绝对约束条件及充分约束条件[8]为

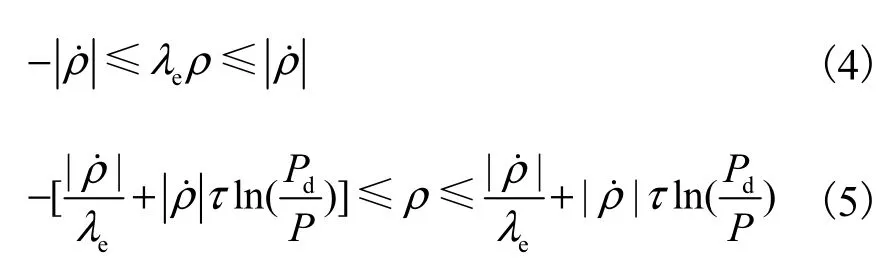
式中：dP为期望达到的功率；P为实际的功率．

1.2 反应性轨迹曲线

1) 控制的可行性

系统能够从给定的功率水平和功率变化率转到一个预期到达的稳态功率水平上，而不出现大的震荡(指过冲和下冲超过指定的允许范围)．

2) 可控性

可控性是指系统在有限时间内，通过一系列的控制可从任意初始状态到达任意最终状态(该定义对中间状态不作限制)．

3) 区别

两者的最大区别在于中间状态的可达性，即控制的可行性的要求要高于可控性，它不仅要求系统可以从初始状态到达最终状态，同时要求系统在各个中间状态依然要达到稳定(没有大的震荡)．

4) 造成原因

上述情况是由缓发中子造成的．因为，当发生裂变时，瞬发中子的数量可以立即确定，但缓发中子数量增加引起的效应却要延迟若干时间后方才显现．

为了使功率控制系统实现控制的可行性，要求对反应堆的动态周期方程加以限制，即当功率到达指定功率时，令该时刻的反应堆周期无穷大(即该时刻中子数量无明显变化)．则由式(3)可得到

通过求解式(6)可得

由式(7)可得到一条反应性随时间变化的轨迹曲线，该曲线为一条稳态情况下的理想曲线．

2 改进型遗传规划算法

2.1 通用遗传规划方法

标准的遗传规划实现过程如下：①根据问题环境先产生一个初始群体(即产生多个由函数和变量随机组成的程序)；②计算群体中的每个个体(计算程序)，根据计算结果与训练集匹配的好坏得到一个适应度值；③以适应度为依据，并利用各种遗传算子(复制、交换、突变)产生下一代个体；④迭代执行上述步骤，直到实现终止条件为止[9]．

在使用遗传规划解决实际问题时，有 4项内容需特别注意．

(1) 适应度函数的确定．

适应度函数直接影响进化的进程，是复制、交换等算子的依据．

(2) 控制参数的选取．

控制参数包括群体内的个体数、最大进化代数、复制概率、交换概率和突变概率等．需特别注意的是，在交换点选取时，树的内外结点选取的概率问题.

(3) 终止条件的设定．

进化是无休止的，除了靠设定最大进化代数强制终止计算外，还可通过设定合理的终止条件来终止计算．如果终止条件合理，问题的解或最优解通常都会出现在最新一代的个体中．

(4) 结果的评价方法．

由于并非所有计算的最优结果都会在最新一代个体中产生(比如计算是通过最大进化代数终止的)，且同一代群体中也会包含多个个体，必须要通过一个合理的结果评价准则来选取得到最优的结果．

2.2 改进后的方法

根据快堆功率控制的一些特点，本文对遗传规划做了相应的改进．

(1) 按照适应度水平划分区间进行复制选择．

通过比较两代个体间的适应度，把个体划分成较好、较差和一般3个子区间．然后对3个区间内的个体再按照适应度大小进行快速排序．最后按一定比例从 3个区间中选出需要复制的个体．先划分空间再排序的方式可节省搜索时间，按适当比例选择又可保证适当的多样性[10]．

(2) 用反应性约束条件确定突变率选取范围．

任何群体的大小都是有限的，因此只有适当选取合适的突变率才能保证最终的收敛．但如果完全随机选择，不仅会消耗大量的计算资源，同时也无法保证突变率的贡献．因此本文采用绝对约束条件(见式(4)，一是实现简单，二是偏安全考虑)为突变率选取划定了一个范围，以保障变异的功能，同时能优化计算时间．

(3) 用反应性轨迹曲线作为结果评价函数．

结果评价函数设置的好坏直接影响到计算终止时是否能选到最优解，而反应性轨迹曲线是一条反应性变化的稳态理想曲线，如果选取结果与其相近就证明结果是最优的[11]．

3 快堆功率控制的遗传规划模型

在建立功率控制的遗传规划模型之前，先要确定一些控制参数．其中，函数集为{＋，－，×，/，lg，sin}；终止符变量为{x1，x2，x3，x4，x5，x6，x7}，分别表示控制棒动作产生的反应性ρact、多普勒效应产生的反应性ρDop、燃料膨胀效应产生的反应性ρswell、冷却剂温度变化产生的反应性ρcool、堆芯径向膨胀产生的反应性ρrad、堆芯弯曲产生的反应性ρbend以及控制棒轴向伸长产生的反应性ρrod．常量集取的是随机常数．初始群体个数为 5,000，最大迭代代数为1,000，最大突变深度为 10，突变率为 9%，交换率为90%，封装率是 1%．初始群体选取时，考虑到单独使用完全法会引入冗余基因，而单独使用生长法又会使个体差异过大，所以采用了把两者相结合的混合法．

该研究以某反应堆功率变化时的控制棒动作产生的反应性及各个反馈反应性作为训练样本集(见表1)，并把样本集送入遗传规划程序进行迭代计算，程序在达到了适应度为1的最佳终止条件后终止，并获得了最佳的预测模型函数(程序中对非法计算项作了限制以避免产生无效输出)，可用树形图表示，如图 1所示．然后，把检验样本集(见表 2)代入最佳预测模型函数，可得到预测值．这时，把预测值和实测值进行比较，如表3所示．

由表3的结果不难看出，总反应性的预测值和实测值的最大误差(误差＝|实测值-预测值|/实测值)保持在1%范围内，结果非常令人满意．

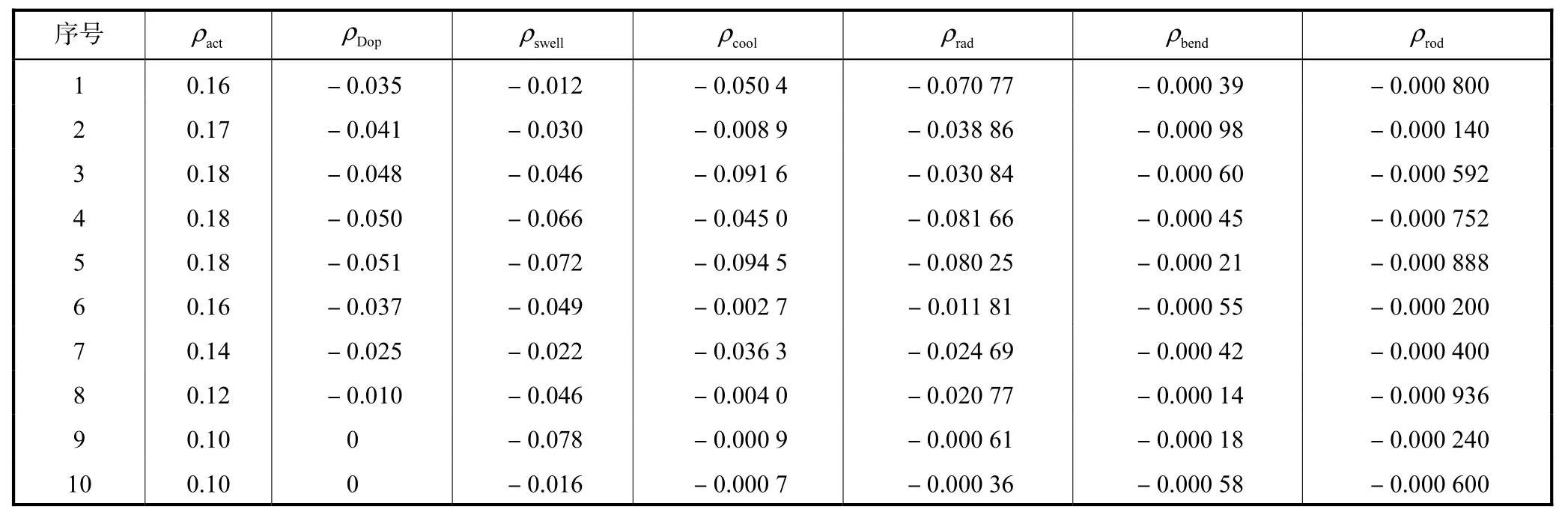
表1 训练样本集Tab.1 Sets of training samples

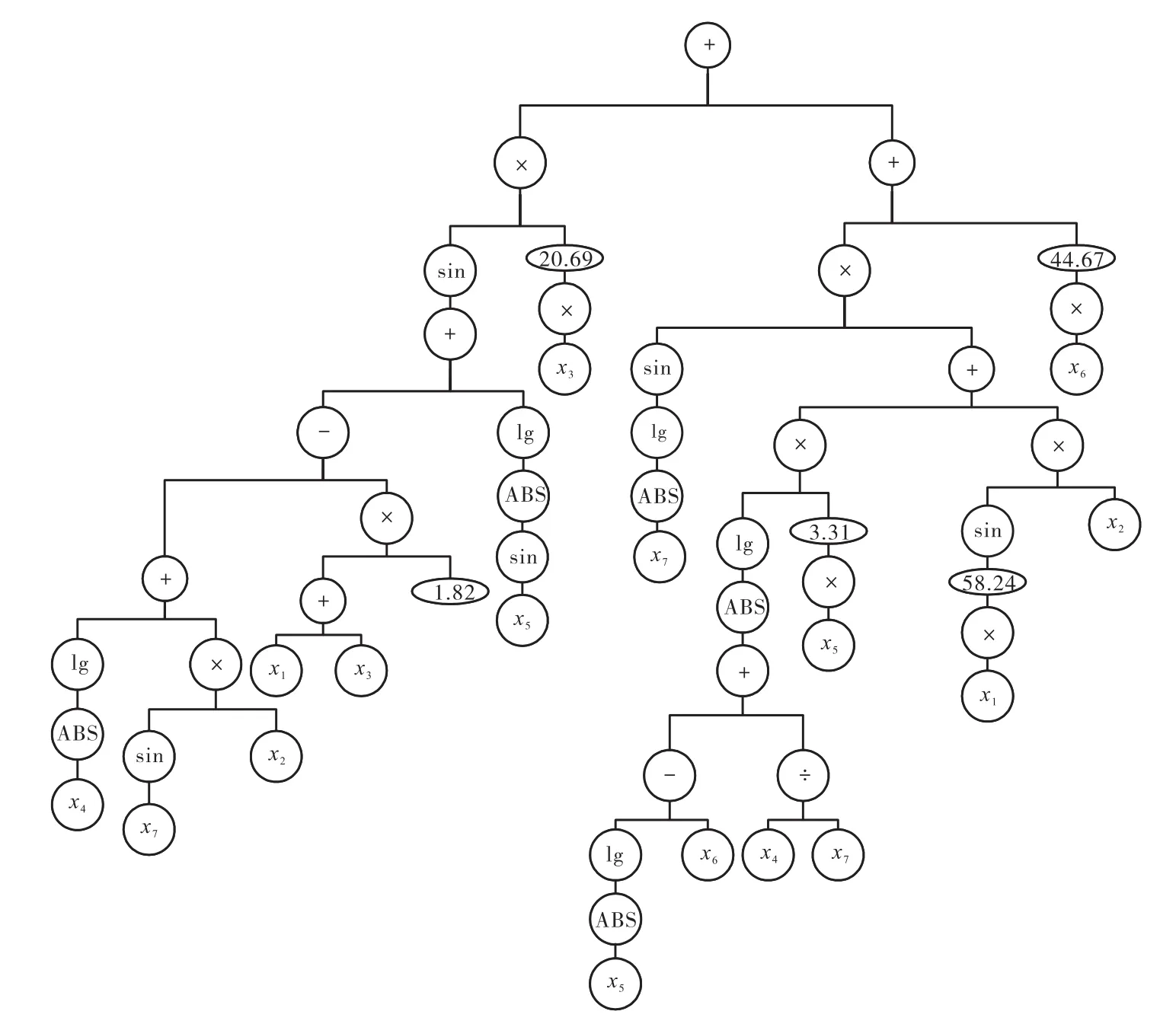
图1 最佳个体树Fig.1 Best individual tree

表2 检验样本集Tab.2 Sets of testing samples

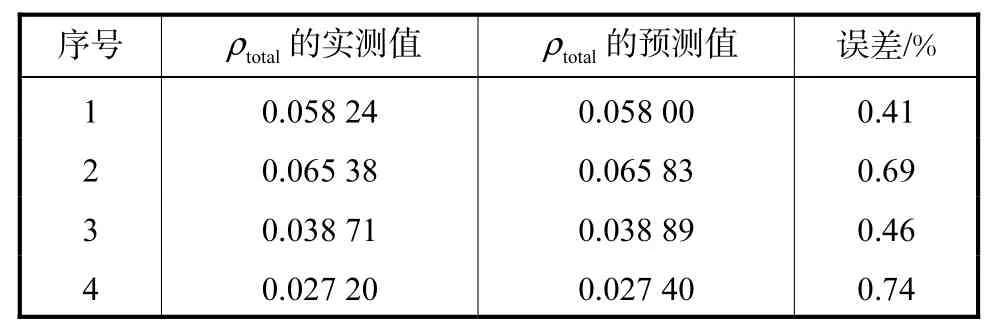
表3 预测值和实测值对比Tab.3 Comparison between predicted values and measured values

4 结 语

预测结果表明，采用这种针对快堆功率控制特性而改进的遗传规划方法与反应堆动态周期方程相结合的方式，在不清楚各种反应性反馈和控制棒动作产生反应性的函数关系的情况下，通过训练样本集可自动产生预测估计函数，且收敛快、精度高．从预测值与实测值拟合良好不难发现，在控制过程中没有大的波动和震荡(反应性被很好地控制在了绝对约束条件内，同时与轨迹曲线贴合紧密)，很好地避免了过冲现象．

［1］ 段天英. 中国实验快堆控制系统的仿真研究[D]. 北京：中国原子能科学研究院，1999.Duan Tianying. Research for Chinese Experimental Fast Reactor Control System by Simulating [D]. Beijing：China Institute of Atomic Energy，1999(in Chinese).

［2］ Bernard J A.Studies on the Closed-Loop Digital Control of Multi-Modular Reactors[M]. USA：MIT Nuclear Reactor Laboratory，1998.

［3］ Gyun N，Belle R U. Application of model predictive control strategy based on fuzzy identification to an SP-100 space reactor [J].Annals of Nuclear Energy，2006，33(2)：1467-1478.

［4］ Ramazan C，Burhanettin C. An expert trajectory design for control of nuclear research reactors [J].Expert Systems with Applications，2009，36(5)：11502-11508.

［5］ Vedat T，Fevzi B. Soft computing technique for power control of Triga Mark-II reactor [J].Expert Systems with Applications，2011，38(1)：11201-11208.

［6］ 谢仲生. 核反应堆物理分析[M]. 西安：西安交通大学出版社，2008.Xie Zhongsheng.Reactor Physics Analysis[M]. Xi’an：Xi’an Jiaotong University Press，2008(in Chinese).

［7］ Bernard J A. An experimental comparison of reactor power controllers based on the standard and alternate formulations of the dynamic period equation [J].IEEE Transactions on Nuclear Science，1987，34(1)：548-552.

［8］ Bernard J A. Dynamic period equation：Derivation，relation to inhour equation，and precursor estimation[J].IEEE Transactions on Nuclear Science，1999，46(1)：433-437.

［9］ 云庆夏，王占权，黄光球. 遗传算法和遗传规划[M].北京：冶金工业出版社，1997.Yun Qingxia，Wang Zhanquan，Huang Guangqiu.Genetic Algorithm and Genetic Programming[M].Beijing：Metallurgical Industry Press，1997(in Chinese).

［10］ Zhang Mengjie，Gao Xiaoying，Lou Weijun. A new crossover operator in genetic programming for object classification[J].IEEE Transactions on Systems，Man，and Cybernetics(Part B)：Cybernetics，2007，37(5)：1332-1343.

［11］ Carlton D，Zhang Mengjie. Execution trace caching for linear genetic programming [C]// IEEE Computational Intelligence Society.Proceedings of the2011IEEE Congress on Evolutionary Computation．New Orleans，USA：IEEE Press，2011：1186-193.