OFDM系统中一种双选择性稀疏信道压缩感知方法

刘开华，陈伟凯，马永涛

(天津大学电子信息工程学院，天津 300072)

正交频分复用(orthogonal frequency division multiplexing，OFDM)是下一代移动通信的核心技术，所采用的多载波高速传输技术允许子信道的频谱相互重叠，从而可以实现极高的频谱利用率．然而，OFDM 系统对相位噪声和载波频偏非常敏感，这对子载波之间的正交性提出了严格的要求．因此，在OFDM 系统接收端，往往需要知道精确的信道状态信息(channel state information，CSI)才能有效对抗信道衰落，实现信号的准确接收．

在实际的无线信号传输中，双选择性的多径信道通常由少数的主要路径簇所主导，因此所呈现的物理信道常具有稀疏特性．而当信号的传输带宽较大或天线个数较多时，信道的稀疏特性尤为明显[1]． 由于稀疏信道只有少数非零抽头，传统的基于导频序列的方法(如基于导频的线性插值和 FFT插值法)极有可能采样到信道的零抽头，而无法准确地插值出信道响应[2]．为了突破传统算法的瓶颈，近几年来，国内外相继有一些学者将压缩感知技术[3-6]应用到对稀疏信道的估计[7-12]中，其中包括 OFDM 系统[9-10]、超宽带(ultra wide band，UWB)系统[11]和水声通信系统[12]等．作为应用数学和信号处理领域的一大突破，压缩感知(compressive sensing，CS)理论表示当信号是可压缩的或是在某个变换域具有稀疏性时，通过采样少量信号就能实现信号的准确或近似重构[3]．在该理论框架下，压缩感知技术可以充分挖掘信道的稀疏特性，能利用非常有限的导频有效地恢复稀疏的信道脉冲响应，在实现对稀疏信道准确估计的同时，还能极大减少导频数目，提高系统的频谱利用率．

在已有的研究成果中，文献[7]最先提出将压缩感知的方法应用到对稀疏信道的估计中去，并具体采用匹配追踪(matching pursuit，MP)算法实现了信道估计．文献[8]研究了在频率选择性条件下对信道进行压缩感知，但是并未将其应用到多载波系统，也并未考虑到信道的时间选择性．文献[9]和文献[10]分别应用群匹配追踪(group matching pursuit，GMP)和子空间追踪(subspace pursuit，SP)的方法对 OFDM 系统进行信道估计，但是二者都没有考虑到时间和频率的双选择性对信道估计的影响．为此，本文重点研究了 OFDM 系统在双选择性衰落下的信道模型，并利用基追踪(basis pursuit，BP)算法[13]实现对稀疏信道的准确重构．在模型的建立过程中，将 OFDM 系统的双选择性信道模型转化为 CS可解的 BPIC(basis pursuit inequality constraint)模型，并利用导频处的信道响应作为 CS重构所需的测量值．仿真结果显示，新方法可以大大减少 OFDM 系统的导频数，且在FFT-Linear和 FFT-FFT二维插值算法无法准确估计出信道响应的同时，BP算法仍能实现较高的估计精度．

1 压缩感知理论

压缩感知技术是针对稀疏信号的新型数据采样和压缩技术，其理论核心可以简述为：对于一个长度为N的一维离散信号 x，若 x是K(K≪N)稀疏的(即只有K个非零元素)，则通过选取合适的测量矩阵以获得x在该矩阵下的线性测量值为

那么仅利用y中的M个测量值就能以很大概率重构原始信号x．由于y的维数要远低于x的维数，因此式(1)有无穷多个解，即该问题是不适定的．然而，Candès等[6]证明，若测量次数M能满足M＝O(Klog(N))，且测量矩阵Φ能满足约束等距条件，则可以通过求解一个最小l0范数问题来重构信号x，即

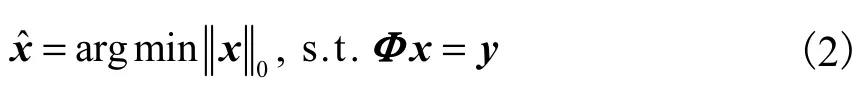
但 Donoho[14]指出，最小l0范数问题仍然是个NP-Hard问题，因而难以求解．为此，研究人员提出了一系列可求得近似最优解的算法，包括MP系列算法[15-17]、BP算法[13]、迭代阈值法[18]以及专门用于图像处理的最小全变分法[3]等．其中，以 MP系列算法和 BP算法最为常用．MP系列算法以贪婪迭代为核心思想，其运算量相对较小，但其理论保证比基追踪算法要弱，并非对所有的信号都能重构，且对测量矩阵的要求比约束等距性更加严格．再者，MP系列算法对维数较低的小尺度信号问题运算速度很快，但对于噪声存在的大尺度问题，重构结果不是很准确，也不具有鲁棒性．考虑实际信道中的噪声条件，为保证OFDM 系统中所有的双选择性衰落信道都能采用压缩感知的方法进行准确估计，本文采用精度更高的BP算法．

BP算法用l1范数替代了l0范数，即得到如下问题：

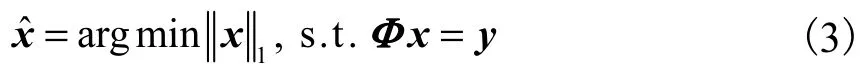
可以证明式(3)和式(2)在理论上是等价的[13].由于问题式(3)实际上是凸优化问题，可以转化为线性规划问题加以求解．如果考虑重构误差及噪声，则可以将式(3)转化为BPIC模型，即

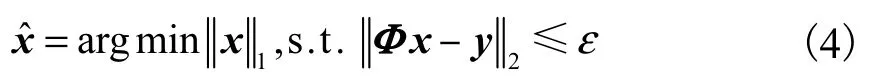
该问题可以利用二阶圆锥规划来求解．

2 双选择性衰落条件下 OFDM系统的信道模型

考虑单天线 OFDM 通信系统，通常情况下该系统可以建模为线性时变系统．在不考虑噪声的情况下，其基带的发射和接收信号的关系为

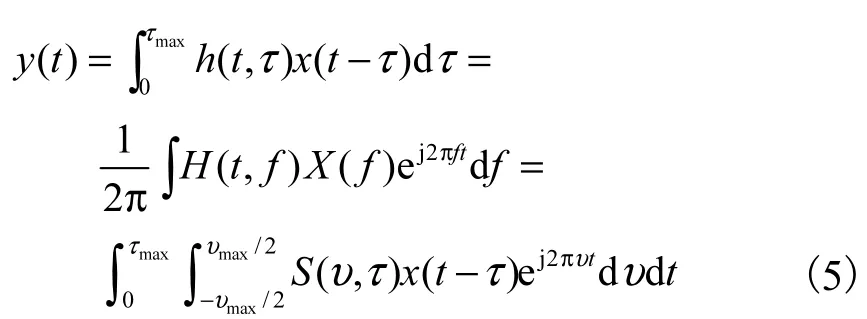
式中：x(t)和y(t)分别表示系统的发射和其对应的接收信号；h(t，τ)代表信道的时变冲激响应；S(υ，τ)是时延-多普勒分布函数；X(f)和H(t，f)分别是对应x(t)和h(t，τ)的傅里叶变换；τmax和υmax是刻画信道特性的重要参数，τmax代表信道所引入的最大时延扩展，而υmax/2则代表信道的最大单边多普勒频移．假设码元的符号宽度为T，基带信号的带宽为W，若信道为时间和频率双选择性信道，则系统的符号宽度和信号带宽都将大于其对应的相干时间 1/υmax和相干带宽 1/τmax，因此存在Wτmax≥1 和Tυmax≥1．

离散的信道时延-多普勒分布函数可用来表征双选择性信道的多径效应和多普勒频移特性，即

式中：Npath表示多径信道中存在的路径总数；αi∈C代表第i个路径的路径增益；υi∈[－υmax/2，υmax/2]和τi∈[0，τmax]分别代表第i个路径中的时延和多普勒频移．因此，双选择性信道的信道响应可以表示为

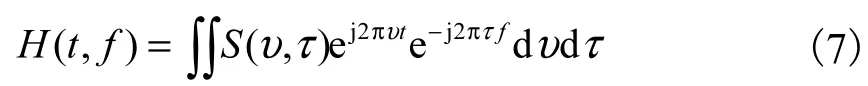
虽然式(6)很好地刻画了物理多径信道的传输特性，但由于它与信道参数 [αi，υi，τi]之间的非线性关系，当存在大量的信道参数时，很难用式(6)进行分析．一般情况下，由于传输系统的带宽及符号时间有限，因此，运用采样定理，信道响应H(t，f)可以用离散参数来近似积分，即

由式(8)可以看出，时延域和多普勒域的最小采样间隔分别为1/T和1/W，而L和K分别代表信道中存在的最大时延数和单边频移数．一个最小采样间隔内的时延分布或频移分布可视为一个时延簇或多普勒频移簇．式(9)中Lτ,l∈{i：τi∈[l/W－1/2,W，l/W＋1/2,W)}和Lυ,k∈{i：υi∈[k/T－1/2,T，k/T＋1/2,T)}分别代表第l个时延簇和第k个多普勒频移簇的路径集合．根据文献[19]所提出的方法，可利用短时傅里叶(short time Fourier，STF)变换基来表征双选择性信道．由于 STF脉冲的持续时间和带宽可以完全拟合双选择性信道的时延和多普勒频移，因此，可将信道响应完全转化为离散形式．设 STF基的最小时域和频域间隔分别为T0和F0，则在时频域内分别有Nt＝T/T0个时域间隔和Nf＝W/F0个频域间隔．设t＝nT0，f＝mF0，则有

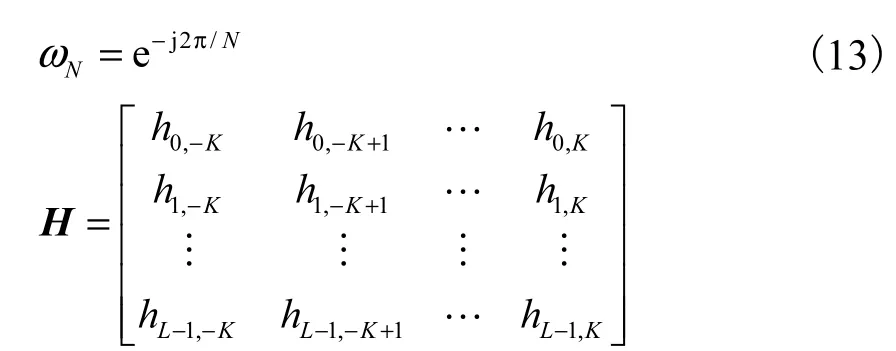
式中：⊗代表矩阵的克罗内克积运算；H是L×(2,K+1)的信道系数矩阵；h＝vec(H)∈CN是信道系数向量，其元素是由H的每行依次衔接而成，即h＝[h0,-K，…，h0,K，h1,-K，…，h1,K，…，hL-1,-K，…，hL-1,K]，由于在双选择衰落条件下，信道呈现稀疏特性，因此，h为稀疏向量，即只有少数非零元素．

基于式(10)，由 Hn,m组成的一维信道响应向量H′可以表示为

式中：H′含有 NtNf个元素；U为 NtNf×L(2,K＋1)维矩阵，其每一行由组成．对于基于导频的信道估计，假设导频插入位置(n，m)∈P，则在接收端可直接估计出在P处的信道响应

式中：Rn,m和 Sn,m分别代表接收符号和导频符号；Zn,m为高斯噪声．设Hp是由导频处信道响应组成的H′的子向量，Up为所对应的维子矩阵，Z为由组成的|P|维向量，则结合式(15)，式(14)可转化为

通过式(16)恢复出信道系数向量h，则最终可通过式(14)得到信道响应向量H′．

3 基于基追踪的信道压缩感知

3.1 传统的二维插值算法

传统的二维插值算法主要分为两步：①先估计插入导频符号处的信道响应(见式(15))；②在①的基础上，根据导频位置的信道估计值进行整个信道的二维内插重构．目前最常用的方法包括线性插值和FFT插值．线性插值算法每次估计只用两个相邻的导频子信道的信道估计值，内插得到两个导频之间的数据子载波的信道响应．线性算法原理简单且易于实现，在实际应用中非常有效，但估计精度比较粗略.

基于 FFT的信道估计算法是目前计算复杂度和性能最为均衡的选择．该算法实现的主要思想是利用在时域补零等效于在频域进行内插的原理，来恢复信道的频率响应．设导频数量为Np，接收端估计出的导频子信道处的信道响应为 Hp(k)，k＝0，1，…，Np－1，将导频子信道处的频率响应变换到时域的冲激响应 hp(n)，n＝0，1，…，Np－1，并在序列 hp(n)的尾部补零得到

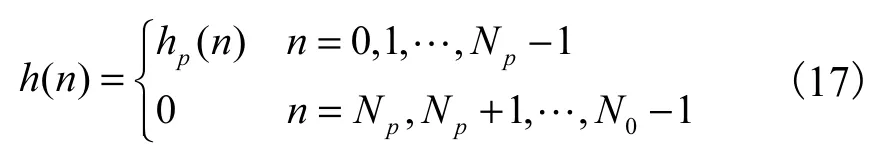
将h(n)变换到频域，则得到信道的频域响应

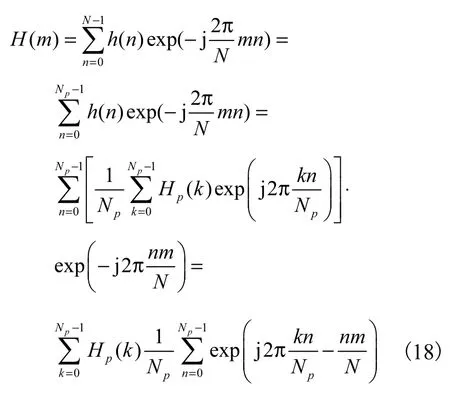
式中N0为符号总数，m＝0，1，…，N-1．

3.2 基于BP算法的稀疏信道估计

本文第 2节已逐步将双选择性衰落条件下的OFDM信道模型转化为基于CS的信号重构模型．令Hp＝y为线性测量值，Up＝Φ 为测量矩阵，并将 Up中的每一列归一化，使其具有单位 l2范数．令 h＝x为待重构的稀疏向量，则式(16)可转化为式(1)中的CS重构模型

式中Z是未知的噪声向量．用BP算法求解考虑了重构误差及噪声的线性规划问题，即将式(19)转化为BPIC模型

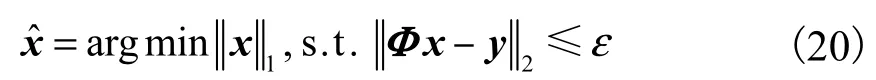
文献[14]已证明式(20)与式(2)的解是等效的，因此应用 BP算法即可求解出稀疏向量 x，即双选择性衰落条件下的信道系数向量 h．由于 BP算法采用内点法求解 l1范数最小化问题，其重构精度较高，且只需少量测量值(即导频处的信道响应值)即可重构信道响应，因而可以有效地减少导频数量，实现频谱利用率的大幅提升．然而，BP算法的算法复杂度也相对较高，设待重构信号长度为 N，测量次数为 M，则算法复杂度为 O(23/2M N )．在本模型中测量矩阵U为NtNf×L(2,K＋1)维矩阵，因此，基于BP算法的信道估计复杂度为

4 仿真结果与分析

在仿真实验中，将基于压缩感知的BP算法与传统的FFT-Linear和FFT-FFT二维联合插值算法进行比较．采用英属哥伦比亚大学(University of British Columbia，UBC)发布的 Matlab SGPL1[19]工具箱中的spg_bpdn(·)函数模拟 BP算法，并将重构误差ε设为1×10-3．FFT-Linear插值算法由两个级联的一维插值算法组成，即先在频率轴上采用 FFT算法插值出信道响应，再利用线性算法在时域轴上进行插值，从而实现整个时频域的信道估计．类似地，FFT-FFT插值算法则是在时频域上皆采用 FFT插值算法，其性能要略好于 FFT-Linear算法，但同时也具有较高的计算复杂度．

假设OFDM系统子载波数为512，循环前缀长度为 128，系统的载波频率为 5,GHz，且每个符号采用64QAM 调制．利用基于空间几何结构的信道仿真工具包IlmProp(IlmProp工具包是由德国伊尔默瑙工业大学电子系开发的功能强大的信道模拟工具包，能根据现实场景参数，如移动台速度、用户场景(农村或城市)等，产生与真实信道逼近的大规模系统级仿真模型)[20]产生模拟现实环境的双选择性衰落信道，所模拟的OFDM传输帧每帧有24个符号．在仿真环境中，设发送端和接收端之间距离 1,500,m，有 10个多径路线并形成3个路径簇(信道稀疏度约为3)，每个路径的时延在(0，τmax)上随机分布，每个路径复增益服从复高斯分布，而且随着路径时延的增大，路径复增益的功率以指数衰减．接收端的移动速度为20,m/s，且与路径簇具有独立同分布的路径导向．

本次仿真实验中，在不同信噪比(SNR)和导频数下，对以上 3种算法的归一化均方误差(MSE)进行了比较，其中导频在传输符号中的插入方式服从均匀分布．图1～图3分别是导频开销为6.25%、12.5%和25%时，各算法的SNR-MSE曲线．

从图中可以看出，无论导频开销是多少，BP算法的估计性能都要远远高于 FFT-Linear和 FFT-FFT插值算法．当导频开销较大且信噪比较小时(见图2(导频开销12.5%)和图3(导频开销25%))，BP算法的优越性并非十分明显，但随着信噪比的不断增加，BP算法的MSE曲线不断下降，而传统的两种算法的估计误差则趋于一条水平的直线，因此 BP算法的性能优势越来越明显．例如，当导频开销为 12.5%、信噪比为40,dB时，BP算法的 MSE可达-42,dB，而传统的插值算法仍只能维持在-16,dB左右．当导频开销仅为6.25%(见图1)时，BP算法在低信噪比时就表现出了算法性能的优越性．当信噪比仅为 5,dB时，传统算法的MSE仅约为-13.5,dB，而BP算法则能达到-16.8,dB．随着信噪比的增大，FFT-Linear和 FFTFFT算法的估计性能仍然没有太大提升，而BP算法在信噪比为22,dB时，其MSE就能达到-21,dB．

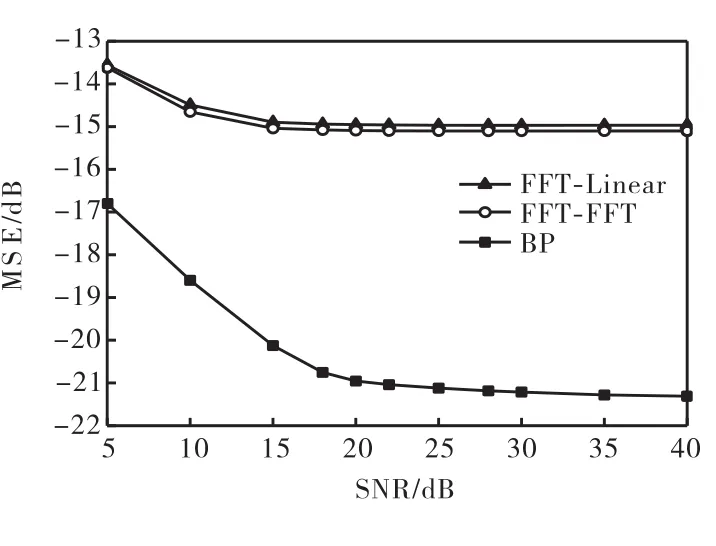
图1 BP与FFT-Linear、FFT-FFT算法MSE性能比较(导频开销6.25%)Fig.1 MSE performance comparison between BP and FFTLinear、FFT-FFT algorithms(Pilot cost is 6.25%)

图2 BP与FFT-Linear、FFT-FFT算法MSE性能比较(导频开销12.5%)Fig.2 MSE performance comparison between BP and FFTLinear，FFT-FFT algorithms(Pilot cost is 12.5%)

图3 BP与FFT-Linear、FFT-FFT算法MSE性能比较(导频开销25%)Fig.3 MSE performance comparison between BP and FFT-Linear，FFT-FFT algorithms(Pilot cost is 25%)

上述实验表明，当物理信道存在强烈的双选择性衰落的情况下(即信道呈现稀疏特性)，传统的 FFTLinear和 FFT-FFT二维插值算法已经不能准确地估计出信道响应，而本文所提出的 BP算法则能利用极少的导频(导频开销仅为 6.25%)实现对双选择性信道的准确估计．因此，可见 BP算法可以极大地减少OFDM 系统中的导频开销，从而实现频谱利用率的大幅提高．

5 结 语

本文提出了一种基于压缩感知技术的OFDM系统信道估计方法．该方法针对双选择性衰落信道多为稀疏信道的特性，将OFDM的信道模型转化为CS可解的重构模型，并利用 BP算法实现了对稀疏信道的准确估计．该法克服了传统二维插值算法无法准确估计稀疏信道的瓶颈，并可大大减少 OFDM 系统的导频数量，提高系统的频谱利用率．仿真实验表明，BP算法的信道估计性能要远高于 FFT-Linear和FFT-FFT二维插值算法，并能在导频数量极其有限的情况下实现对双选择性稀疏信道的精确估计．

［1］ Raghavan V，Hariharan G，Sayeed A M. Capacity of sparse multipath channels in the ultra-wideband regime[J].IEEE Journal of Selected Topics in Signal Processing，2007，1(3)：357-371.

［2］ Yang B，Cao Z，Letaief K B. Analysis of lowcomplexity windowed DFT-based MMSE channel estimator for OFDM systems[J].IEEE Transactions on Communications，2001，49(11)：1977-1987.

［3］ Candès E J，Romberg J，Tao T. Robust uncertainty principles：Exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory，2006，52(2)：489-509.

［4］ Donoho D L. Compressed sensing[J].IEEE Transactions on Information Theory，2006，52(4)：1289-1306.

［5］ Baraniuk R G. Compressive sensing [J].IEEE Signal Processing Magazine，2007，24(4)：118-120.

［6］ Candès E J，Tao T. Decoding by linear programming[J].IEEE Transactions on Information Theory，2005，51(12)：4203-4215.

［7］ Cotter S F，Rao B D. Sparse channel estimation via matching pursuit with application to equalization[J].IEEE Transactions on Communications，2002，50(3)：374-377.

［8］ Bajwa W U，Haupt J，Raz G，et al. Compressed channel sensing[C] //Proceedings of Annual Conference on Information Sciences and Systems. Princeton，NJ，2008：5-10.

［9］ Wu C J，Lin D W. A group matching pursuit algorithm for sparse channel estimation for OFDM transmission[C]//International Conference on Acoustic，Speech and Signal Processing. Toulouse，France，2006：14-19.

［10］ Qi C H，Wu L N. Digital broadcast channel estimation with compressive sensing[J].Journal of Southeast University：English Edition，2010，26(3)：389-393.

［11］ Paredes J L，Arce G R，Wang Z. Ultra-wideband compressed sensing：Channel estimation[J].IEEE Journal of Selected Topics in Signal Processing，2007，1(3)：383-395.

［12］ Berger C R，Zhou S，Preisig J C，et al. Sparse channel estimation for multicarrier underwater acoustic communication：From subspace methods to compressive sensing[J].IEEE Transactions on Signal Processing，2010，58(3)：1708-1721.

［13］ Chen S B，Donoho D L，Saunders M A. Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing，1998，20(1)：33-61.

［14］ Donoho D L. For most large underdetermined systems of linear equations，the minimall1-norm solution is also the sparsest solution[J].Communications on Pure and Applied Mathematics，2006，59(6)：797-829.

［15］ Tropp J，Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory，2007，53(12)：4655-4666.

［16］ Needell D，Vershynin R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit [J].Foundations of Computational Mathematics，2009，9：317-334.

［17］ Donoho D L，Tsaig Y，Drori I，et al. Sparse Solution of Underdetermined Linear Equations by Stagewise Orthogonal Matching Pursuit [EB/OL]. http：//www. dsp.ece. rice. edu/cs/，2011-11-20.

［18］ Herrity K K，Gilbert A C，Tropp J A. Sparse approximation via iterative thresholding[C] //International Conference on Acoustics，Speech and Signal Processing(ICASSP). Washington，USA，2006：624-627.

［19］ Friedlander M，van den Berg E. Toolbox SPGL1[EB/OL]. http：//www. cs. ubc. ca/labs/scl/spgl1，2011-11-20.

［20］ Ilmenau University of Technology. IlmProp Project[EB/OL]. http：//tu-ilmenau. de/ilmprop，2011-11-20.