基于改进的GM(2，1)模型的粮仓温湿度预测

赵新蕖 刘亚卓 张丽伟

基于改进的GM(2，1)模型的粮仓温湿度预测

赵新蕖1刘亚卓1张丽伟2

(河南机电高等专科学校1，新乡 453000)
(新乡学院2，新乡 453000)

建立粮仓温湿度的预测模型，对实现粮食的安全储备有着积极意义。但粮仓温湿度数据的贫乏性和其随季节变化的波动性，一直是困扰粮仓温湿度建模的难题，这也使粮仓的温湿度控制一直处于被动局面。利用灰模型贫数据建模的特点，提出了采用改进的GM(2，1)模型对粮仓检测到的温湿度数据进行建模分析的方法，得到粮仓的温湿度预测模型，实现对粮仓温湿度变化趋势的预测和预警。仿真结果表明，该模型的预测值有较高的精度，因此，有一定的实用价值。

改进的GM(2，1)模型 温湿度预测 预警 粮食储备安全

中国是一个粮食大国和人口大国，粮食在国民经济中占有显著地位，是关系国计民生、国家安全和社会稳定的特殊产品，中国粮食安全对世界粮食安全的影响举足轻重。那么粮食的安全储藏就至关重要。现今我国粮食储藏却存在粮情测控系统兼容性差、功能简单的问题。

灰模型自问世以来，以其对数据量要求少;对数据的分布规律要求低;建模不受数据性质影响等优点，日益受到大家的重视［1－3］。灰色预测就是通过对原始数据的处理和灰色模型的建立，发现、掌握系统的发展规律，对系统的未来状态做出科学的定量预

测［4－5］。

本研究讨论了用改进的GM(2，1)模型［6－7］对粮仓检测到的数据进行分析，实现对粮仓温湿度变化趋势的预测，以实现对粮仓温湿度的有效控制。这对维护我国的粮食安全有着重要的意义。

1 改进的GM(2，1)模型的构造原理及一般步骤

改进的GM(2，1)模型从原始序列X(0)出发，根据积分的几何意义，对X(0)进行一次累加构造其积分序列X(1)，再进一步构造X(1)的紧邻均值序列Z(1)，两者均为X(0)的背景值;根据微分的几何意义，对X(0)进行一次累减构造其微分序列a(1)X(0)，从而建立反映X(0)、X(1)和a(1)X(0)之间微积分关系的二阶白化微分方程，离散化得到由X(0)、Z(1)和a(1)X(0)构成的线性方程组。由此方程组出发，用最小二乘法确定出二阶白化微分方程的系数。通过求解白化微分方程并离散化，得到其积分序列的预测公式，再对其进行一次累减还原，得到原始序列的预测公式。

设原始序列X(0)={X(0)(1)，X(0)(2)，…，X(0)(n)}

1．1 原始数据处理

①累加生成:对X(0)进行一次累加得X(1)={X(1)(1)，X(1)(2)，…，X(1)(n)}，其 中X(1)(k)=

②累减生成:对X(0)进行一次累减得a(1)X(0)={a(1)X(0)(2)，a(1)X(0)(3)，…，a(1)X(0)(n)}，其中a(1)X(0)(k)=X(0)(k)－X(0)(k－1);k=2，3，…，n。

1．2 建模

由X(1)构造紧邻均值序列Z(1)={Z(1)(2)，Z(1)(3)，…，Z(1)(n)};其中Z(1)(k)=0．5［X(1)(k)+X(1)(k－1)］，k=2，3，…，n 。

于是得到改进GM(2，1)模型的白化微分方程:

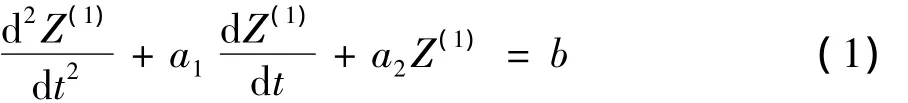
离散化得:

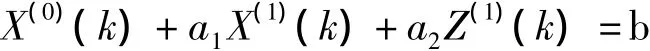
1．3 求解参数a1，a2，b

用最小二乘法，可解得公式＜2＞中的参数a1，a2，b

令

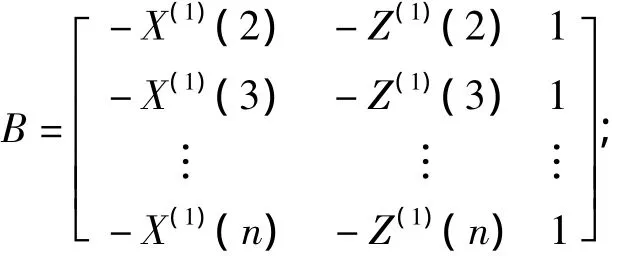
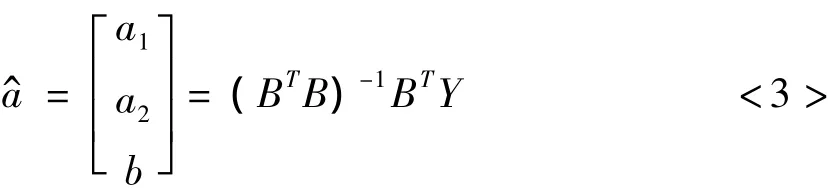
则

1．4 参数的二次估计

1．4．1 零不是特征方程的特征根

下面仅以特征方程有两个不相等的特征根r1、r2(r1、r2都不等于零)为例。

令

1．4．2 零是特征方程的根

以零是特征方程的单根为例:

代入Z(1)(k)，令则

2 基于改进的GM(2，1)模型的粮仓温湿度预测仿真

这里节选了某粮仓春秋两季粮堆温度和粮仓相对湿度的数据［8］，利用改进前和改进后的GM(2，1)模型分别进行仿真，每次对最新的5个数据点建模，并根据该模型对下一时刻的数据进行预测。在PC机上Matlab6．5环境下仿真，结果如表1和表2所示。其中，预测值列中t≤5的数据为拟合值，从t≥6时刻开始的值均为采用该时刻前的5个采样点的数据建模型后得到的预测值。

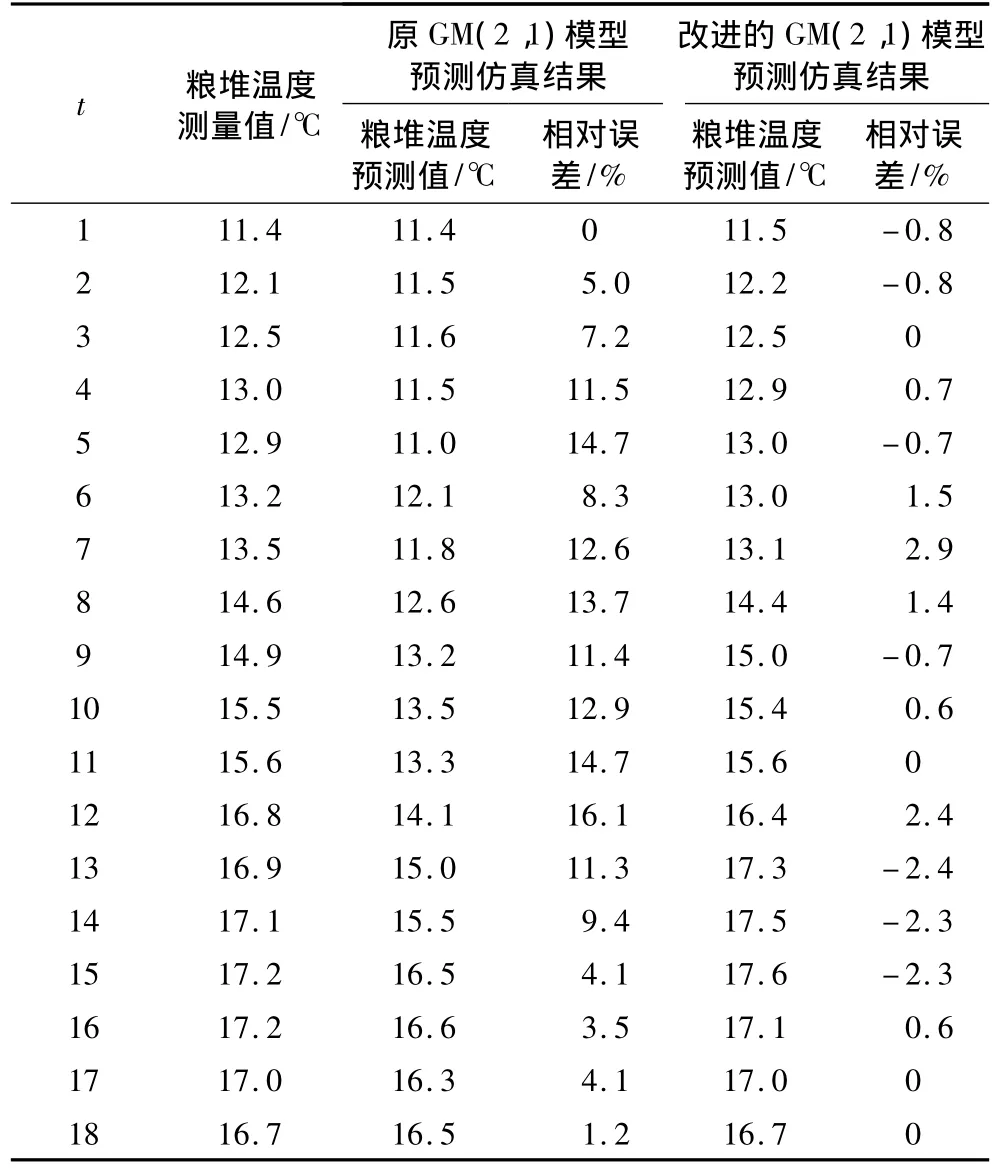
表1 2种GM(2，1)模型进行粮仓温度预测的仿真结果

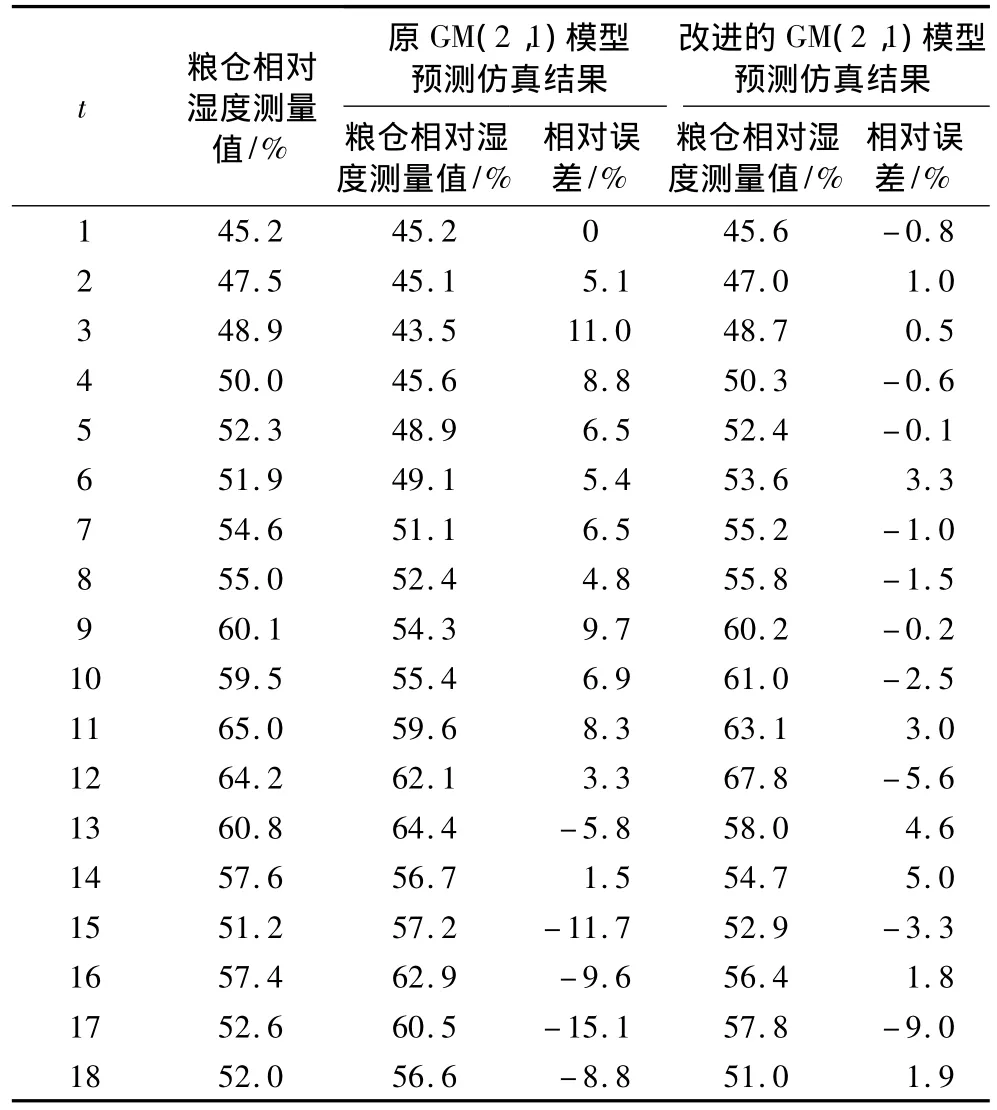
表2 2种GM(2，1)模型进行粮仓湿度预测的仿真结果

从表1和表2显示的数据比较可以看出，用改进后的GM(2，1)模型对粮堆内的温度进行预测时，其相对误差的最大值不超过3%，用该模型对粮仓相对湿度值进行预测时，其相对误差的最大值不超过10%;而用改进前的GM(2，1)模型对粮堆内的温度进行预测时，其相对误差的最大值甚至达到了16．1%，用该模型对粮仓相对湿度值进行预测时，其相对误差最大值也会高达15．1%。

将2种模型得到的拟合值、预测值和实际测量值做图比较，如图1所示。从图1可以看出，除了温湿度变化较大的时刻外，使用改进的GM(2，1)模型的预测精度要远远高于改进前的原GM(2，1)的预测精度，总体而言，模型的预测效果是良好的。因此，如果将改进后GM(2，1)模型用于对粮仓温湿度控制的实时预警，即可以降低对原始数据的个数要求，又有较高的精度保证，具有一定实际意义。

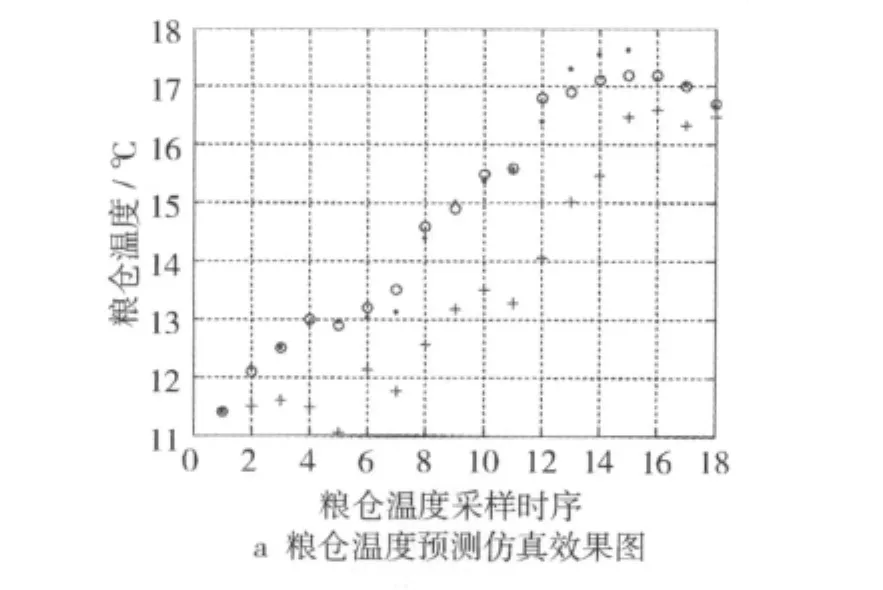
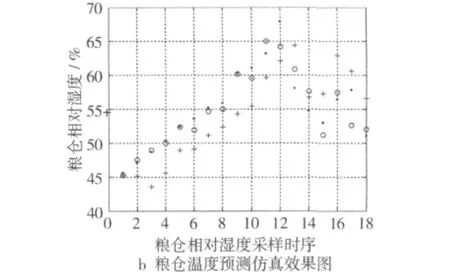
图1 基于改进GM(2，1)模型的粮仓温湿度预测仿真效果图

3 结论

本研究提出了基于改进的GM(2，1)模型对粮仓温湿度参数进行实时预测，从而为粮仓温湿度控制提供预警的方法。仿真结果表明，该方法能够根据较少的原始数据有效地预测粮仓温湿度参数的发展趋势，在对粮仓温度数据进行建模预测时，相对误差的最大值不超过3%，在对粮仓相对湿度进行建模预测时，其相对误差的最大值不超过10%。因此，将该预测模型用于粮仓的温湿度控制，对保证粮食存储安全有一定的积极意义。

［1］邓聚龙．灰色控制系统［M］．武汉:华中工学院出版社，1987:330－337

［2］刘思峰，郭天榜，党耀国，等．灰色系统理论及其应用［M］．第2版．北京:科学出版社，2000(8):126－133，117

［3］邓聚龙．灰色系统基本方法［M］．武汉:华中理工大学出版社，1996

［4］邓聚龙．灰预测与灰决策［M］．修订版．武汉:华中科技大学出版社，2002

［5］肖新平，宋中民，李峰．灰技术基础及其应用［M］．北京:科学出版社，2005

［6］赵新蕖，陈红林．GM(2，1)模型预测公式的改进研究［J］．武汉理工大学学报，2006，28(10):125－127

［7］唐松云，陈绵云．插入值方法的灰色建模［J］．武汉理工大学学报，2005，2(27):87－89

［8］王帅．粮仓智能监控系统的设计与实现［D］．成都:电子科技大学，2010．

The Forecasts of Temperature and Humidity of the Barn Based on the Improved GM(2，1)

Zhao Xinqu1Liu Yazhuo1Zhang Liwei2
(Henan Mechanical and Electrical Engineering College1，453000)
(Xinxiang University2，Xinxiang 453000)

It has a positive meaning for food security to establish the prediction model of temperature and humidity of granary．Because of the deficient and fluctuation with season of the granary temperature and humidity data，it has been in a passive situation for modeling．In this paper，a new method is proposed that uses improved GM(2，1)model to analyze the temperature and humidity data，and to get the forecast model，in order to forecast the future trend of storage conditions of the barn．It uses the deficient data modeling character of gray model．The simulation results show that the forecasts of the model is high accuracy，therefore，the method has a certain practical value．

the improved GM(2，1)，the forecasts of the temperature and humidity，advance warning，food security storage

N945．12

A

1003－0174(2012)08－0085－04

时间:2012－08－20 10:48

网络出版地址:http://www．cnki．net/kcms/detail/11．2864．TS．20120820．1048．002．html

2012－01－01

赵新蕖，女，1978年出生，讲师，大系统建模