数学史视角下的数学教学探析

● (杭州师范大学初等教育学院 浙江杭州 310018)

●王德胜 (邹城市中心店中学 山东邹城 273512)

数学史视角下的数学教学探析

●李国强(杭州师范大学初等教育学院 浙江杭州 310018)

●王德胜(邹城市中心店中学 山东邹城 273512)

1 数学史在数学教学中的地位

数学教师在数学课堂上讲解数学知识，可以有很多方式，如:通过数学新旧知识之间的逻辑联系引出新知识；利用学生生活中的实例使抽象的数学知识具体化、形象化；利用数学史料激发学习热情或感悟数学思想方法，以促进学生对数学知识的理解和掌握；还可借助数学游戏，调动学生的好奇心，激发学生学习数学的兴趣；也可通过数学实验增加学生的亲身体验，促进数学知识的掌握；……具体如图1所示：

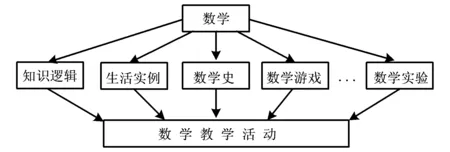
图1

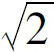
2 数学史视角下的教学内容重组及教学活动开展

数学教科书为追求知识的系统性，注重数学知识逻辑关系的介绍，通常省略数学知识的形成背景和发展过程．教师在教学中若遵从教科书内容，往往导致学生不理解数学知识的来龙去脉及其学习意义．数学家莱布尼茨曾说：“没有什么比看到发明的源泉更重要了，这比发明本身更重要．”教师运用数学发展的顺序来组织数学知识，有利于学生发现“数学概念、结构、观点是怎样被‘发明’用来作为一种工具，组织物理社会和思维世界的现象”．学生学习数学概念、结构、观点时，借助数学史能够从它们为什么被“发明”中获得动机．不仅如此，数学史还可以通过最少的逻辑代沟、最自然的方式描述数学．因此，利用数学史料重新组织教科书中的知识是教师组织教学内容的重要方式．

例如，高中数学教科书中一般先介绍指数再介绍对数，导致很多学生认为对数的概念是人们通过指数的关系硬性规定的，对数运算性质也是由指数运算法则推导而来的.对数的产生纯属于数学逻辑体系自身发展的结果，与社会生活无关．为此，在教学中，可以按照数学的历史产生轨迹先学习对数，再学习指数，这样，学生不仅能够了解对数、指数的产生过程，正确认识指数、对数的概念，还有助于体会对数的实际应用和当时的社会价值．

另外，教师可以运用数学史料更好地组织课堂教学．例如，高中教科书中在推导自然数前n项求和公式时运用了逆序相加的方法，这一方法虽然简捷，但是学生难以想到，而且较抽象．一位教师为了让学生从“数”、“形”2个角度更全面地掌握自然数前n项求和公式的推导过程，在讲解完教科书上的方法后，又运用数学史上借助直观、形象几何图形推导的方法进一步解释．教学过程如下：

首先，问题情境．

教师引导学生探索下列问题，这些是自然数的前n项和的特例．

1+2=

1+2+3=

1+2+3+4=

1+2+3+4+5=

…

1+2+3+4+5+…+n=

其次，归纳结论．

(1)引入古希腊毕达哥拉斯学派的“三角形数”(如图2).

图2

生：第1个图形表示的数是1；第2个图形表示的是1+2；第3个图形表示的是1+2+3；第4个图形表示的是1+2+3+4．

师：用图形表示数的方法在公元前6世纪就已经出现．当时，古希腊毕达哥拉斯学派把自然数与小石子堆放的形状相比拟．图2中表示的数称之为“三角形数”，它们正好表示从1开始的多个连续自然数之和．同学们想一想，能否用图形来计算自然数的和？

(可提示学生将“三角形”补成平行四边形．)

图3

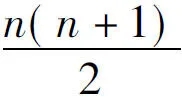
(2)运用我国古代传统的“垛积术”解决.

我国古代数学家杨辉发展了中国传统的“垛积术”，他把这一问题中各项之间的结构规律用相似结构的“垛”来比拟(如图4)．将“垛”补成方形(如图5)，十分直观、形象地化未知为己知，从而求得问题的解．可让学生累加长方体木块，找出规律．

把这一问题进一步推广到一般的情形，即

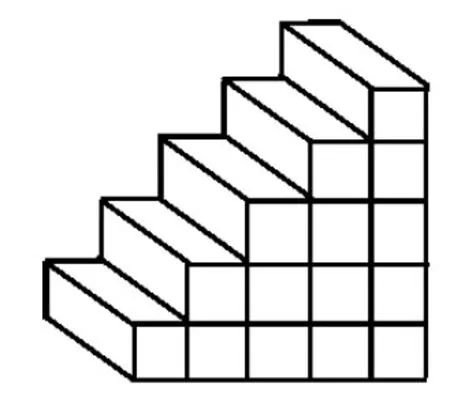
图4

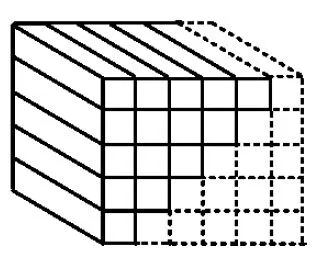
图5

最后，数学证明．

用数学归纳法进行证明(略)．

法国著名数学家庞加莱主张“科学史应该是我们的指南”．同样，数学史也应是数学教学的指南．由前面的阐述和教学案例可以看出，依托数学史开展课堂教学可以看作是一种数学教学的设计理念和实施取向，它可以充分利用丰富的史料，让学生从数学发展的视角学习数学，更全面、更深刻地掌握数学知识，提高数学教学效果．

3 数学史视角下的数学知识分类及其教学策略

在数学发展的历程中，有些新产生的知识是对原有知识的再精细和再深化.例如，相对于“角度制”，后出现的“弧度制”虽与“角度制”相通，但“弧度制”可极大简化原来感觉繁琐的三角计算，这一新知识的出现为很多数学家所接受，这类知识称之为常规时期的数学知识．但也有些知识，它们的产生对原有知识、原有思维观念造成剧烈冲击，甚至是颠覆性的．例如，无理数的出现使得毕达哥拉斯学派的信条“万物皆数”陷入危机；非欧几何的出现使得欧氏几何的许多结论不再成立，等等，这类知识称之为革命时期的数学知识．教学中，教师应根据知识的特点采取不同的教学方法．

(1)在教学常规时期的数学知识时，引入数学史应重在讲授数学的研究方法.如前所述，常规时期的数学知识与原有知识在认知观念上变化不大．根据皮亚杰的认知发展理论，学生学习这些知识时，可充分利用原有认知结构去同化新知识，而无需重新建立新的认知结构．因此，这类知识的教学难点不是学生能不能理解新知识，而在于如何让学生获得建立在这些新概念、新结论上的研究方法．

例如，解析几何是高中数学的重要内容，也是数学的重要研究分支．从历史上看，解析几何的出现虽然极大地推动了数学发展，特别是代数与几何的融合，但是它与原有的几何知识、方程知识联系密切，且是一脉相通，因此它属于常规时期数学知识的范畴．教学解析几何时，学生对新概念的理解问题不大，教学重点应放在让学生体会“数形结合”这一重要思想方法和掌握“任何问题→数学问题→代数问题→方程求解”的解决问题的思维方法．在数学发展中，数学家为探索或研究解析几何，留下了许多的有价值的经典问题，教师对数学史中的经典问题或题目加以改编并运用于数学教学，对学生领会“数形结合”思想方法的实质、感悟解析几何在解决实际问题中的优势及其在数学发展中的价值都是非常有用的．借助史料，学生还可以透过数学知识和真理“冰冷的外表”，了解隐含在其背后的数学史上曾经“火热的思考”，学到“活”的、“有生机”的数学.这有助于营造出一个渴望认知、不断探索且极富吸引力的学习情境，并易进入学生的心灵，从而激发学生学习数学的原动力．

(2)在学习革命时期的数学概念时，引入数学史介绍概念的来龙去脉.在数学史上，数学家们理解革命时期的数学知识，尚需改变认识论和方法论，改变其科学观念．对于学生而言，要了解这些知识更是谈何容易．在教学中，教师要想方设法改变学生原有的认知结构或创建新的认知结构，采用顺应学习的方式获得新知识．最可行的方法就是：在讲授这些新概念时，引入数学史，讲清楚新概念的产生、发展过程.目前的教材对这方面内容的介绍非常欠缺，因此，在讲解革命时期的数学概念时，引入相关数学史是十分必要的．

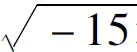
通过介绍虚数的发展过程，学生将会了解到虚数概念的来龙去脉，认识到虚数发展的历程．特别是这些数学史对于学生理解虚数概念、掌握虚数的运算法将是有益的补充和重要的调和剂．

数学史有助于教师区分不同类型的数学知识．上面针对2类不同的数学知识提出的2种结合数学史的教学方法，是数学课堂教学的有益参考．但要强调一点，2类数学知识不是完全割裂开来的，2种教学方法的区分不是绝对的．在教学中，应做到针对某类数学知识，采用有针对性的教学方法，而不能过于偏废．概念教学与数学解题应贯穿在整个数学教学之中．

综上所述，从数学史的视角探析数学教学，不仅是数学史与数学教育研究的重要方面，而且对于优化数学教学方式，促进学生更好地学习数学，进而提高数学教学质量，都有着积极的现实意义．

[1]侯新杰.物理学史与物理教学结合的理论与实践研究[D].上海：华东师范大学，2005：39-40.

[2]张维忠,汪晓勤.文化传统与数学教育现代化[M].北京：北京大学出版社，2006：210-218.

[3]朱凤琴,徐伯华.数学史融入数学教学模式的国际研究与启示[J].数学教育学报，2010(3)：22-25.

杭州师范大学科研启动经费项目2011QDW215)