一类不等式奥林匹克试题的共同背景

● (春谷中学 安徽南陵 241300)

一类不等式奥林匹克试题的共同背景

●邹守文(春谷中学 安徽南陵 241300)

通过对一些数学奥林匹克不等式的分析，发现一些不等式的共同背景，即在p,q,r为正实数，且p2+q2+r2+2pqr=1的条件下证明某个不等式，经研究得到该条件下的若干性质，据此可以证明一类不等式.

结论1设p,q,r为正实数，且p2+q2+r2+2pqr=1，则

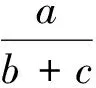
即

∑a(a+b)(a+c)≥2∑ab(a+b)，

得

∑a(a-b)(a-c)≥0.

最后一式为Schur不等式.

(第48届国家集训队测试题)

证明令u=4p2,v=4q2,w=4r2，则已知式变形为p2+q2+r2+2pqr=1，所证式等价于

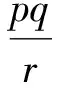
此即结论1.

例2设正实数x,y,z满足xy+yz+zx+xyz=4，求证：x+y+z≥xy+yz+zx.

(1996年越南数学奥林匹克试题)

证明令xy=4p2，yz=4q2,zx=4r2,则已知式变形为

p2+q2+r2+2pqr=1，

所证式等价于

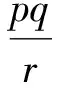
此即结论1.

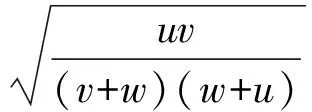
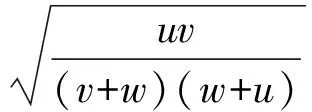
例3设a,b,c≥1，且满足abc+2a2+2b2+2c2+ca-cb-4a+4b-c=28,求a+b+c的最大值.

(2011年全国高中数学联赛加试B卷试题)

a+b+c=a′+1+b′-1+c=a′+b′+c=4(p+q+r)≤6,

故a+b+c的最大值是6.

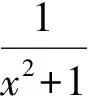
(2007年美国国家集训队试题，2005年伊朗数学奥林匹克试题)

证明已知条件可转化为x2y2+y2z2+z2x2+2x2y2z2=1，令xy=p，yz=q,zx=r,则已知式变形为

p2+q2+r2+2pqr=1，

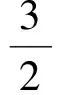
结论3设p,q,r为正实数，且p2+q2+r2+2pqr=1，则p+q+r≥2(pq+qr+rp).

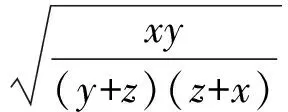
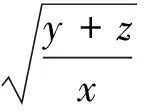
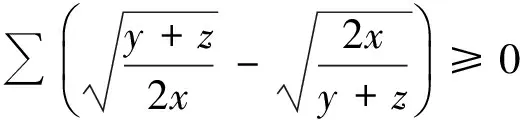
因为

所以结论3成立.

(2011年中欧数学奥林匹克试题)

证明已知式变形为abc=a+b+c+2，即

p2+q2+r2+2pqr=1，

且

于是所证式等价于

即

p+q+r≥2(pq+qr+rp)，

此即结论3.

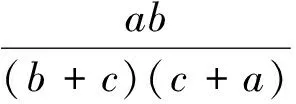
由平均值不等式得

结论3成立.

例6设非负数x,y,z满足x2+y2+z2+xyz=4,证明：xy+yz+zx-xyz≤2.

(第30届美国数学奥林匹克试题)

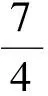
证明由条件p2+q2+r2+2pqr=1，可作变换p=cosA，q=cosB,r=cosC，这里A，B，C为锐角△ABC的3个内角，则所证式等价于在锐角△ABC中

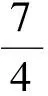
因为

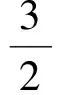
所以

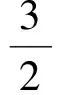
而cosA+cosB+cosC≥1+4cosA·cosB·cosC等价于

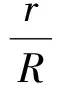
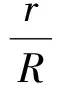
由于

同理可得

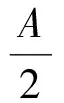
上述3个式式相乘得

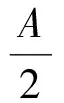
故结论5成立.

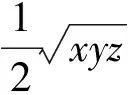
(2004年全国高中数学联赛河南省预赛试题)

证明已知条件可以作变换x=16p2,y=16q2,z=16r2，则已知和求证分别变形为：设p,q,r为正实数且p2+q2+r2+2pqr=1，求证：

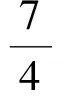
此即结论5.

[1] 邹守文.一道48届国家集训队测试题的研究[J].中国初等数学研究，2011(3)：108-112.

[2] 陈建兵,邹守文.一个条件等式派生的不等式在证明竞赛不等式试题中的运用[J].中学数学研究，2011(5)：46-49.