赋值法在作截面交线中的应用

● (象山中学 浙江象山 315700)

赋值法在作截面交线中的应用

●李左杰(象山中学 浙江象山 315700)

我们知道，作截面图形是立体几何中的一个难点,而作截面图形的关键是作出截面与被截几何体的交线.为解决这一难点，笔者给出一种用赋值法作截面交线的方法．此法简捷、精确，凸显了“解析几何思想”和“算法思想”.

所谓赋值法求截面交线，就是在空间直角坐标系中，确定截面上的点应该满足的方程(简称截面方程)，然后通过被截几何体各面的特征，对相应的坐标变量赋值，进而给出截面在被截几何体各面上的交线,最后得出截面的图形．

例1如图1，P是空间中任意一个动点.若P到正方体ABCD-A1B1C1D1的棱CD所在直线与到棱A1D1所在直线的距离相等，求动点P在正方体各面所在平面上的轨迹．

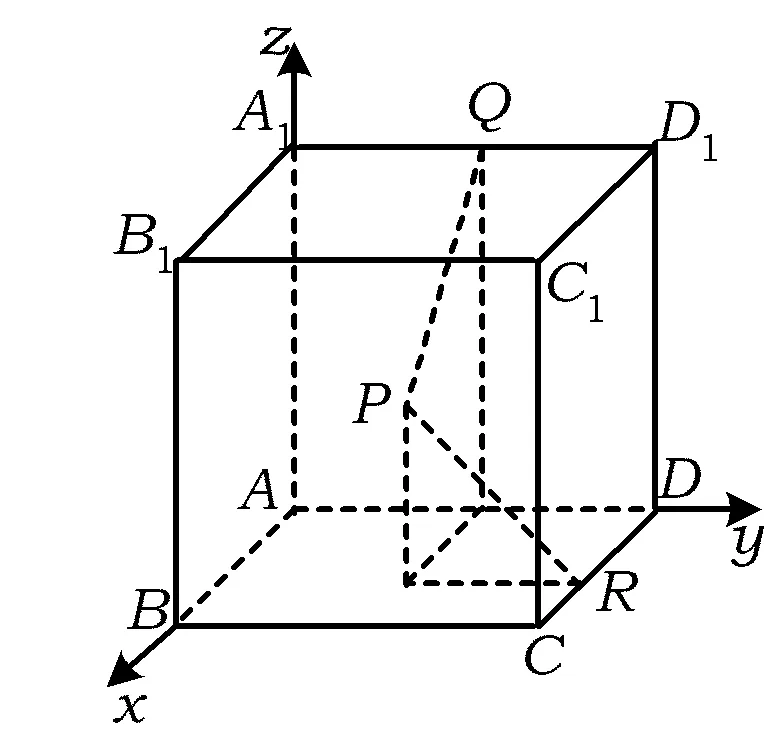
图1

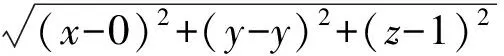
整理得

2z=x2-y2+2y.

令x=0，则2z=-y2+2y，即点P在平面ADD1A1上的轨迹是抛物线；令x=1，则2z=-y2+2y+1，即点P在平面BCC1B1上的轨迹是也是抛物线.

令y=0，则2z=x2，即点P在平面ABB1A1上的轨迹是抛物线；令y=1，则2z=x2+1，即点P在平面CDD1C1上的轨迹也是抛物线.

令z=0，则x2-y2+2y=0，即点P在平面ABCD上的轨迹是双曲线；令z=1，则x2-y2+2y=2，即点P在平面A1B1C1D1上的轨迹是双曲线．

注解决本题的关键是建立空间直角坐标系，求出动点P的轨迹方程.这样，动点P在正方体各面所在平面上的轨迹就是该轨迹方程和各平面方程联立方程组的解.因此，赋值法求截面交线的方法充分体现了解析几何的思想方法.

例2如图2,已知正方体ABCD-A1B1C1D1中，AA1=2，P为底面ABCD的中心，Q，R分别为棱DD1，A1B1的中点，求截面PQR与正方体各面的交线．

图2

分析如图2建立坐标系，则P(1，1，0)，Q(0，2，1)，R(1，0，2)，且

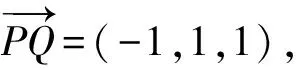
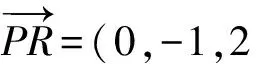
设平面PQR的法向量为n=(a,b,c)，则

解得法向量为

n=(3,2,1).

令M(x,y,z)为平面PQR内的任意一点，则

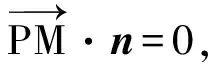
即

3(x-1)+2(y-1)+z=0,

化简得 3x+2y+z-5=0.

(1)

为了得到截面与底面ABCD的交线方程，令z=0,则方程(1)可化为

3x+2y-5=0,

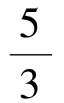
同理，分别令x=0，y=0,y=2,z=2,得到平面PQR与正方体的面ADD1A1，A1B1BA，C1D1DC，A1B1C1D1的4条交线:

它们依次围成一个五边形．

注截面与正方体各面的交线，实际上就是求2个平面的交线.在空间中，求平面方程的关键是找出该平面的一条法向量，然后利用法向量与平面中的任一向量垂直列出平面方程.利用赋值法求截面交线能较好地解决正方体中过不共线的任意3个点的截面问题.

(2007年全国高中数学联赛试题)

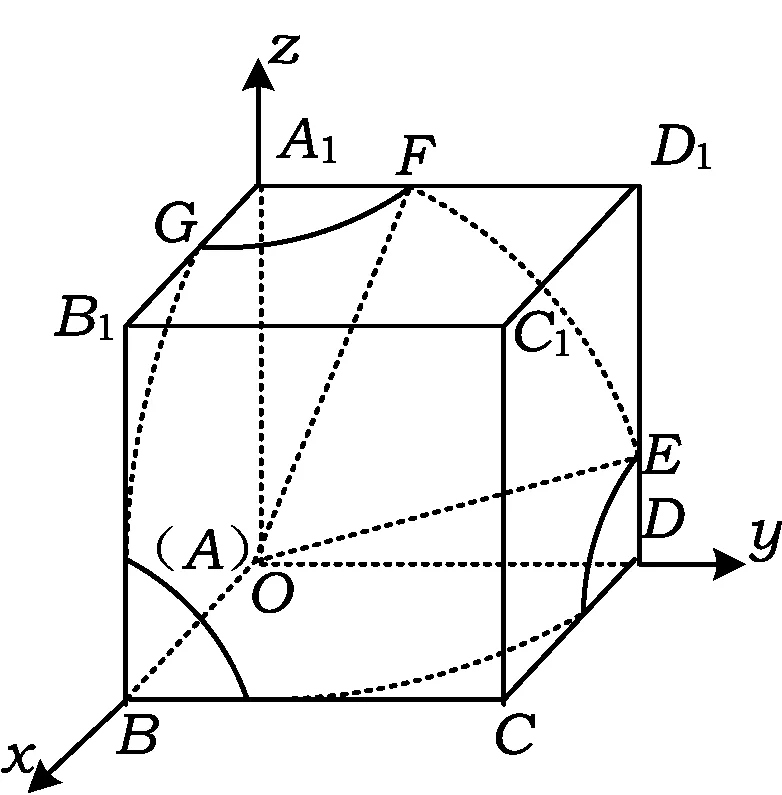
图3

如图3建立空间直角坐标系,令球面上点的坐标为P(x,y,z)，则

分别令x=0，y=0,z=0,得球面与坐标平面yOz,xOz,xOy的3条等长的交线:

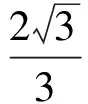
分别令x=1,y=1,z=1,得球面与平面B1C1CB,CDD1C1,A1B1C1D1的3条交线：

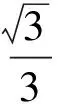
如图3所示，在面AA1D1D上，因为

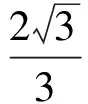
所以

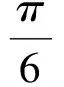
同理可得

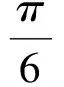
因此

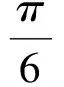
这样的弧共有3条．

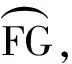
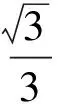
这样的弧也有3条．

于是，所得的曲线长为

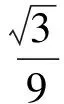
注建立空间直角坐标系，求出动点P所满足的轨迹方程，再将平面方程和该轨迹方程联立，消元后即得截面交线的方程.利用赋值法求截面交线，将立体几何的截面问题程序化，充分凸显了高中数学的“算法思想”.

例4圆锥的轴截面SAB是边长为2的等边三角形，O为底面中心，M为SO的中点，动点P在圆锥底面内(包括圆周).若AM⊥MP，则点P形成的轨迹的长度为

( )

(2008年浙江省高中数学竞赛试题)

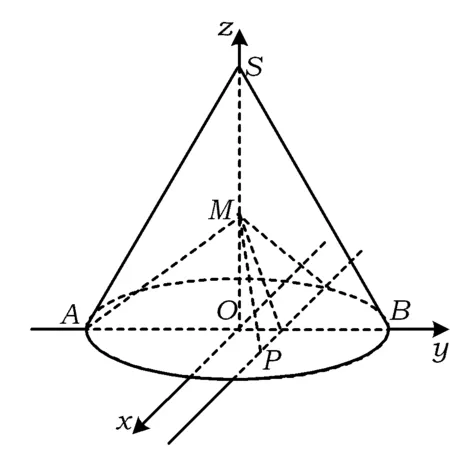
图4

因为AM⊥MP，所以

即

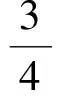
故选B.

笔者认为，用赋值法作截面交线降低了学生作截面的难度，同时对发展学生的空间想象能力和运算求解能力有较大的帮助，值得向学生介绍．