对2011年重庆数学高考文科第15题的深入研究
2012-11-20松江区第二中学上海201600
● (松江区第二中学 上海 201600)
对2011年重庆数学高考文科第15题的深入研究
●卫福山(松江区第二中学 上海 201600)
2011年重庆市数学高考文科第15题如下:
原题若实数a,b,c满足2a+2b=2a+b,2a+2b+2c=2a+b+c,则c的最大值是________.
文献[1]利用换元法并结合均值不等式加以解答,给出了较为简单的导数法以及判别式法.本文给出了该题的其他解法,并作一定的变式研究.
1 考题的另解
解利用均值不等式
由2a+2b=2a+b及均值不等式,知

即
2a+b≥4(2a+b≤0显然不能成立).
由2a+2b+2c=2a+b+c,得
2a+b+2c=2a+b·2c,
即

解得

从而
cmax=2-log23.
2 变式研究
文献[1]换元后得出该题的等价问题:
问题1已知正数x,y,z满足x+y=xy,x+y+z=xyz,求z的最大值.
实际上,在另解的基础上,可以利用不等式的性质解决,具体如下:
解由x+y=xy及均值不等式,得

即
xy≥4.
于是由x+y+z=xyz,得

由xy≥4,得
xy-1≥3
从而
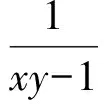
即
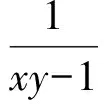
因此
此外,考题中的3个正实数a,b,c,能否推广呢?笔者推广到了4个及更多的正实数,得到如下问题:
问题2已知正数a,b,c,d满足a+b=ab,a+b+c=abc,a+b+c+d=abcd,求d的最大值.


问题3已知正数a1,a2,…,an满足a1+a2=a1a2,a1+a2+a3=a1a2a3,…,a1+a2+…+an=a1a2…an,求an的最大值.





…
猜想

下面用数学归纳法对以上结论加以证明.
当n=3时,问题3即为“已知正数a1,a2,a3满足a1+a2=a1a2,a1+a2+a3=a1a2a3,求a3的最大值.”类似于问题1的做法,由
a1+a2=a1a2,
得

即
a1a2≥4.
由a1+a2+a3=a1a2a3,得
即

而此时当n=3时,

即结论成立.
假设当n=k(k≥3)时结论成立,即

为证当n=k+1时结论成立,首先需要做3个铺垫性的工作:
(1)数列{an}的每一项均大于1.


由已知条件得
转化为
即
得

从而

(3)数列{an}从第2项起是递减数列.
这是因为当n≥2时,结合递推公式有
从而

又数列{an}的每一项均大于1,故an+1 结合以上(1)~(3),得 由归纳假设知 于是 即证 亦即证 即证 上式显然成立,从而说明以上的归纳对n=k+1也成立. 从以上推广研究中,可以发现满足条件的数列还有几个有趣性质: 已知正数a1,a2,…,an满足a1+a2=a1a2,a1+a2+a3=a1a2a3,…,a1+a2+…+an=a1a2…an,则 (1)数列{an}的每一项均大于1; (3)数列{an}从第2项起是递减数列; [1] 安振平,韩小平.2011年重庆高考数学文科第15题解法探讨[J],数学通讯:上半月,2011(9):8-9. [2] 卫福山.对一个优美不等式的证明及联想[J].中国数学教育:高中版,2012(5):44-46.




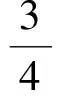



3 几个有趣的结论


