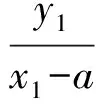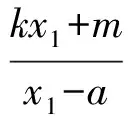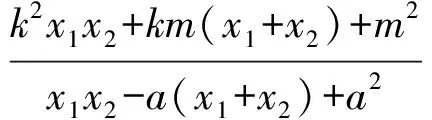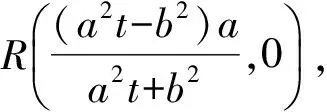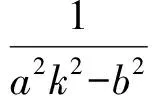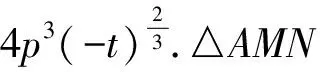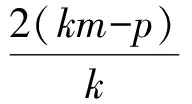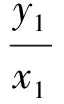一道竞赛模拟试题引发的探究

● (漳州市第一中学 福建漳州 363000)

一道竞赛模拟试题引发的探究

●林新建(漳州市第一中学 福建漳州 363000)

本刊2012年第6期给出了如下一道竞赛模拟试题：

本文对此作一般性的探究，给出顶点斜率积为定值的三角形面积取得最值的几个结论，兹介绍如下.

(b2+a2k2)x2+2a2kmx+a2(m2-b2)=0.

由Δ>0，得a2k2+b2>m2.设M(x1,y1)，N(x2,y2)，则

于是

y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=

当点A为长轴的端点时，不妨设A(a,0)，则

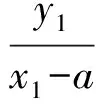
因为kAM·kAN=t，所以

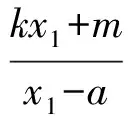
即

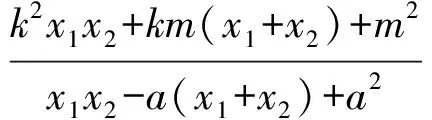
亦即

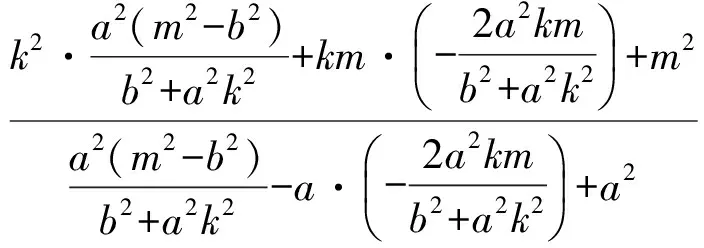
化简得

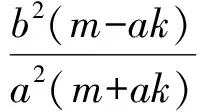
从而

因此直线MN的方程为

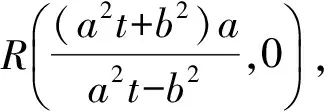
当点A为短轴端点时，不妨设A(0,b)，则

因为kAM·kAN=t，所以

即

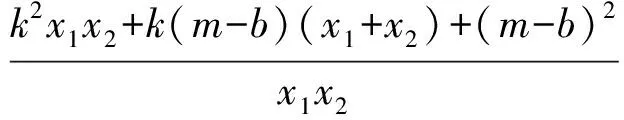
亦即

化简得

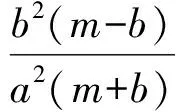
从而

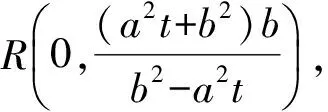
运用性质1，原竞赛题的解为：

特别地，当t=-1时，AM⊥AN，可得：

(b2-a2k2)x2-2a2kmx-a2(m2+b2)=0.

由Δ>0，得

a2k2-b2

设M(x1，y1)，N(x2,y2),则

于是

y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=

因为A(a,0)，所以

因为kAM·kAN=t，所以

即

亦即

化简得

从而

因此直线MN的方程为

因此△AMN的面积不存在最大值与最小值.

当MN不与x轴垂直时，可设直线MN的方程为y=kx+m，代入y2=2px并整理,得

k2x2+2(km-p)x+m2=0.

由Δ>0，得2km

于是

因为A(0,0)，所以

因为kAM·kAN=t，所以

即

特别地，当t=-1时，AM⊥AN，得到：

推论2设A为抛物线E：y2=2px(p>0)的顶点，点M，N在抛物线E上，且满足AM⊥AN，则△AMN面积存在最小值，且最小值为4p2.△AMN面积不存在最大值.