对一道调考压轴试题的探究

● (黄石市第一中学 湖北黄石 435000)

对一道调考压轴试题的探究

●杨瑞强(黄石市第一中学 湖北黄石 435000)

2012年湖北省武汉市武昌区高三数学调研考试的压轴题如下：

(1)若函数f(x)在定义域内为增函数，求实数p的取值范围；

(2)解猜想：当n∈N*时，

下面给出证明：

bn=Sn-Sn-1=2ln(n+1)-2lnn=

2[ln(n+1)-lnn]，

当n=1时，b1=S1=2ln2，适合上式．因此，

bn=2[ln(n+1)-lnn](n∈N*).

由第(1)小题，可知取p=1，则

f(x)≥f(1)(x≥1)．

即

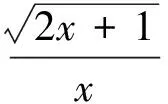
在上式中分别取k=1,2,3,…,n，并将同向不等式相加，得

综上所述，当n∈N*时，

(3)证明同第(2)小题，当n≥2时，记

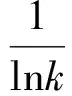
x-1≥lnx．

设g(x)=x-1-lnx，x∈(0,2)，则

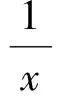
函数g(x)在(0,1)上递减，在(1,2)上递增，从而

g(x)≥g(1)=0，

即x-1≥lnx在x∈(0,2)时恒成立.

综上所述，当x∈(0,+∞)时，

x-1≥lnx(当且仅当x=1时等号成立)．

(1)

用x代换x-1，得

x≥ln(x+1)(当且仅当x=0时等号成立)．

(2)

当k≥2且k∈N*时，由式(1)，得

k-1≥lnk>0，

从而

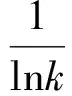
由式(2)，得

k>ln(k+1)，

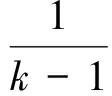
故当k≥2且k∈N*时，

即

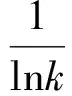
在上式中分别取k=1,2,3,…,n，并将同向不等式相加，得

(1)用a表示出b,c；

(2)若f(x)≥lnx在[1,+∞]上恒成立，求a的取值范围；

(2010年湖北省数学高考理科试题)

(3)

再来看一个运用“对比分项比较法”直接构造函数，证明此类和型不等式的例子：

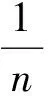
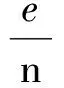
当n=1时，b1=S1=1，适合上式．因此，bn=1-lnn(n∈N*)．原问题等价于：

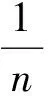
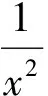
当x≥1时，f′(x)≥0恒成立，函数f(x)在[1,+∞)上单调递增，因此f(x)≥f(1)=0，即

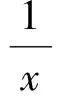
分别令x=1,2,3…,n，相加即得

故对于任意正整数n，均有