用函数视角证明不等式

● (衢州市第二中学 浙江衢州 324000)

用函数视角证明不等式

●舒金根(衢州市第二中学 浙江衢州 324000)

不等式证明是竞赛的热点问题之一,由于证明方法多、技巧性强,因而也是竞赛的难点之一.用函数视角证明不等式是一种有效的方法.通过构造函数,利用函数的性质或与导数等其他知识相结合,能达到事半功倍的效果.

1 构造函数,结合函数的性质解题

(2010年全国高中数学联赛加试试题)

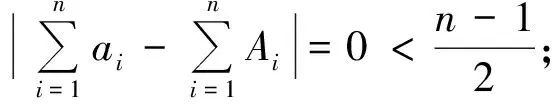
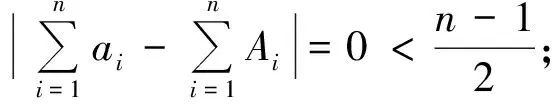
因为

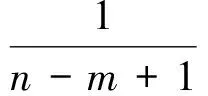
所以

其中k=m或k=n-m.因ai>0(1≤i≤n),故上式等号不能成立，即

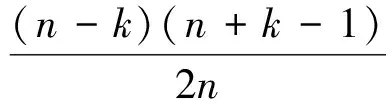
于是

2 构造函数,结合导数知识解题

例2设a,b,c>0,求证:a5+b5+c5≥5abc(b2-ac).

分析视a5+b5+c5-5abc(b2-ac)为b的函数.

证明(1)当b2≤ac时,a5+b5+c5≥5abc(b2-ac)成立.

(2)当b2>ac时,设f(b)=a5+b5+c5-5abc(b2-ac),则

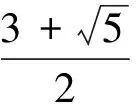
即

a5+b5+c5≥5abc(b2-ac).

3 构造函数,结合函数图像的切(割)线解题

(第8届香港奥林匹克竞赛试题)

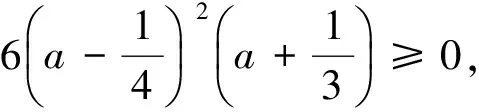
即

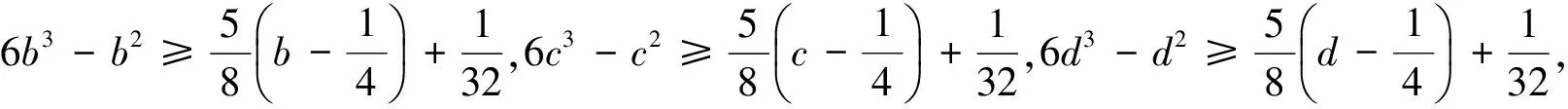
相加,得

例4若ai(i=1,2,…,n,且n≥3)为满足a1a2…an=1的正数,求证:

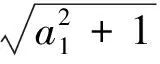
分析设ai=exi(i=1,2,…,n),则问题转化为:

已知x1+x2+…+xn=0,求证:

结合上述分析,回归到原问题,即有如下证明方法.

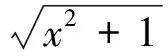
当x>1时,f′(x)<0,当00,故f(x)≤f(1),即

4 构造函数,结合微积分知识解题

(2009年全国高中数学联赛加试试题)

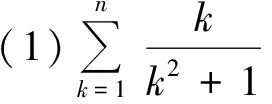
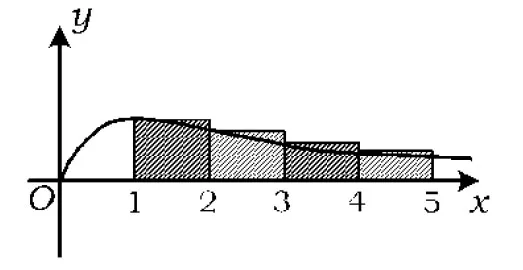
图1

图2

从而

又当n=1时,得

综上所述