几个典型空间轨迹问题的探讨

郑剑光 (浙江省台州市路桥中学,浙江 台州 318050)

几个典型空间轨迹问题的探讨

郑剑光 (浙江省台州市路桥中学,浙江 台州 318050)

在中学数学中，轨迹问题是立体几何中重要问题之一，它体现了立体几何与解析几何的交汇，不仅是“能力立意”命题新理念下的新素材，也是高考题常常涉及的内容。从几何与解析2个角度讨论了几道有代表性求解空间轨迹问题。空间轨迹问题的探讨不仅涉及一题多解，而且进一步给出问题的再发展，极大地丰富了这些问题的内涵，同时也是拓展思维的好办法。

平面几何；立体几何；解析几何；轨迹

1 几何法

如果轨迹问题的条件是通过几何方式给出的, 并且结论也是以几何的方式表达,那么就可以考虑用立体几何、平面几何的知识及方法求轨迹，而不涉及建立直角坐标系。

例1[1](2004年重庆高考题) 若三棱锥A-BCD的侧面ABC内一动点P到底面BCD的距离与到棱AB的距离相等，则动点P的轨迹与△ABC组成的图形可能是( )。

方法1图形A可以按如下方法排除, 如果P在AC上时到底面BCD的距离与到棱AB的距离相等，那么当点在AC上沿图形A所示的轨迹运动到B点的开始阶段,P到底面BCD的距离小于P在AC上时到底面BCD的距离,而P到棱AB的距离大于P在AC上时到棱AB的距离相等,因此至少P在AC上沿图形A运动到B点的开始阶段,到底面BCD的距离与到棱AB的距离不相等。 所以可以排除图形A。 完全类似可以排除图形B。所以答案只可能是C, 或是D。 因为P到棱BC的距离大于P到底面BCD的距离,换句话说P到棱BC的距离大于P到棱AB的距离,所以∠PBCgt;∠PBA,因此答案选D。

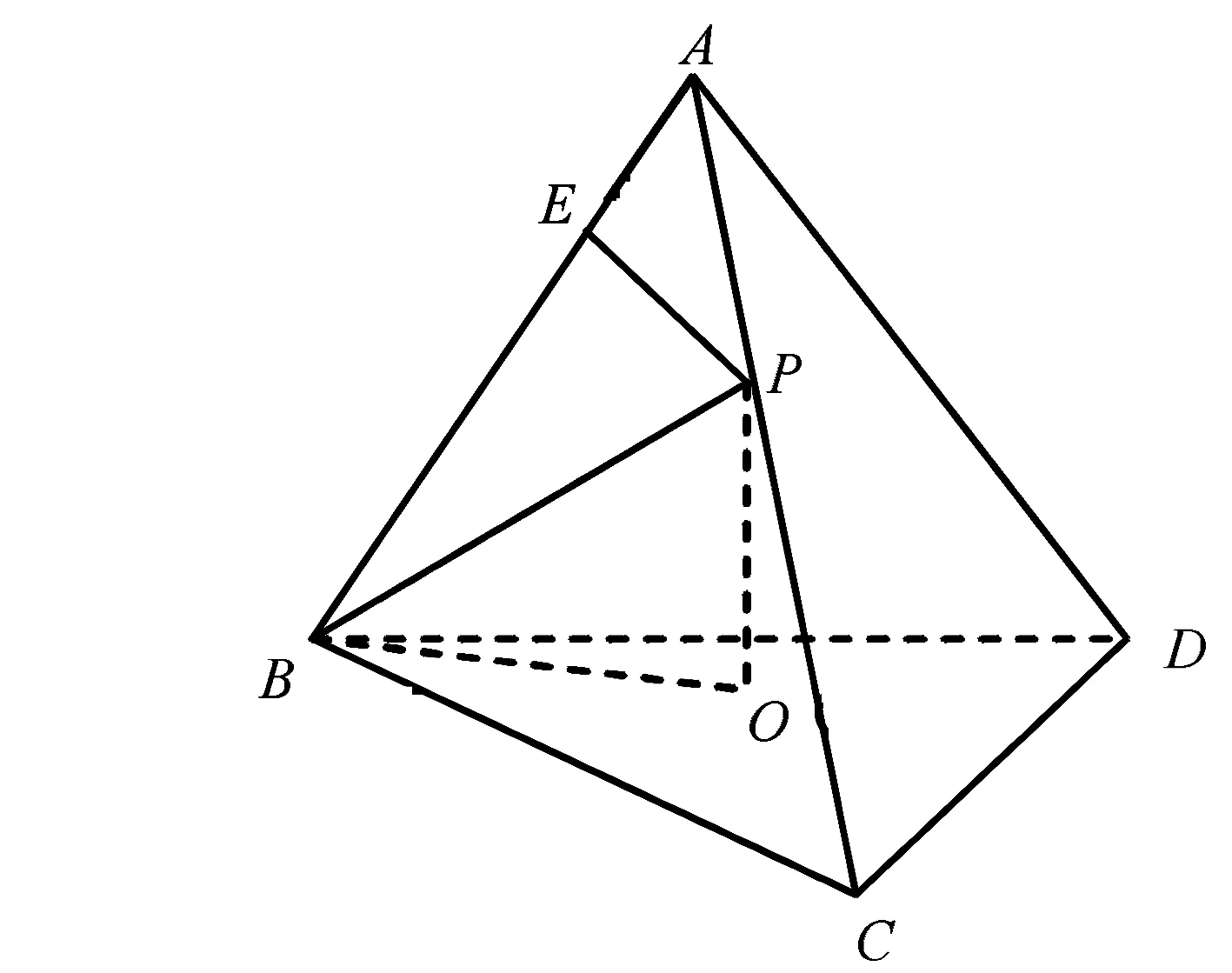
图1 例1示意图

方法2因为P到棱BC的距离与P到底面BCD的距离的比是大于1的常数,从而得P到棱BC的距离与P到棱AB的距离的比是大于1的常数, 因此答案选D。

方法3如图1,设点P在AC上,作PO⊥平面BCD于O，BE⊥AB于E，因为PO=PE，所以∠PBE=∠PBO，若P′为BP上任一点，则P′到底面BCD的距离与到棱AB的距离相等，又由最小角定理，知∠P′BA=∠P′BOlt;∠P′BC,故选D。

例1的进一步拓展若三棱锥A-BCD的侧面ABC内一动点P到底面BCD的距离和到棱AB的距离之比为正常数k,则动点P的轨迹在△ABC组成的图形依然是以B为一端点,另一端点在棱AC

上的线段。若k增大, 则P的轨迹向棱AB移动, 若k减速,P的轨迹向棱AB移动,特别地,k→+∞时P的轨迹以棱AB为极限;k→0+时P的轨迹以棱BC为极限。

例2[2-3]在正方体ABCD-A1B1C1D1中,E为AA1中点,点P在对角面BB1D1D内运动(图2),若EP总与直线AC成等角,则点P的轨迹可能是( )。

A.圆或圆的一部分 B.椭圆或椭圆的一部分

C.抛物线或抛物线的一部分 D.双曲线或双曲线的一部分

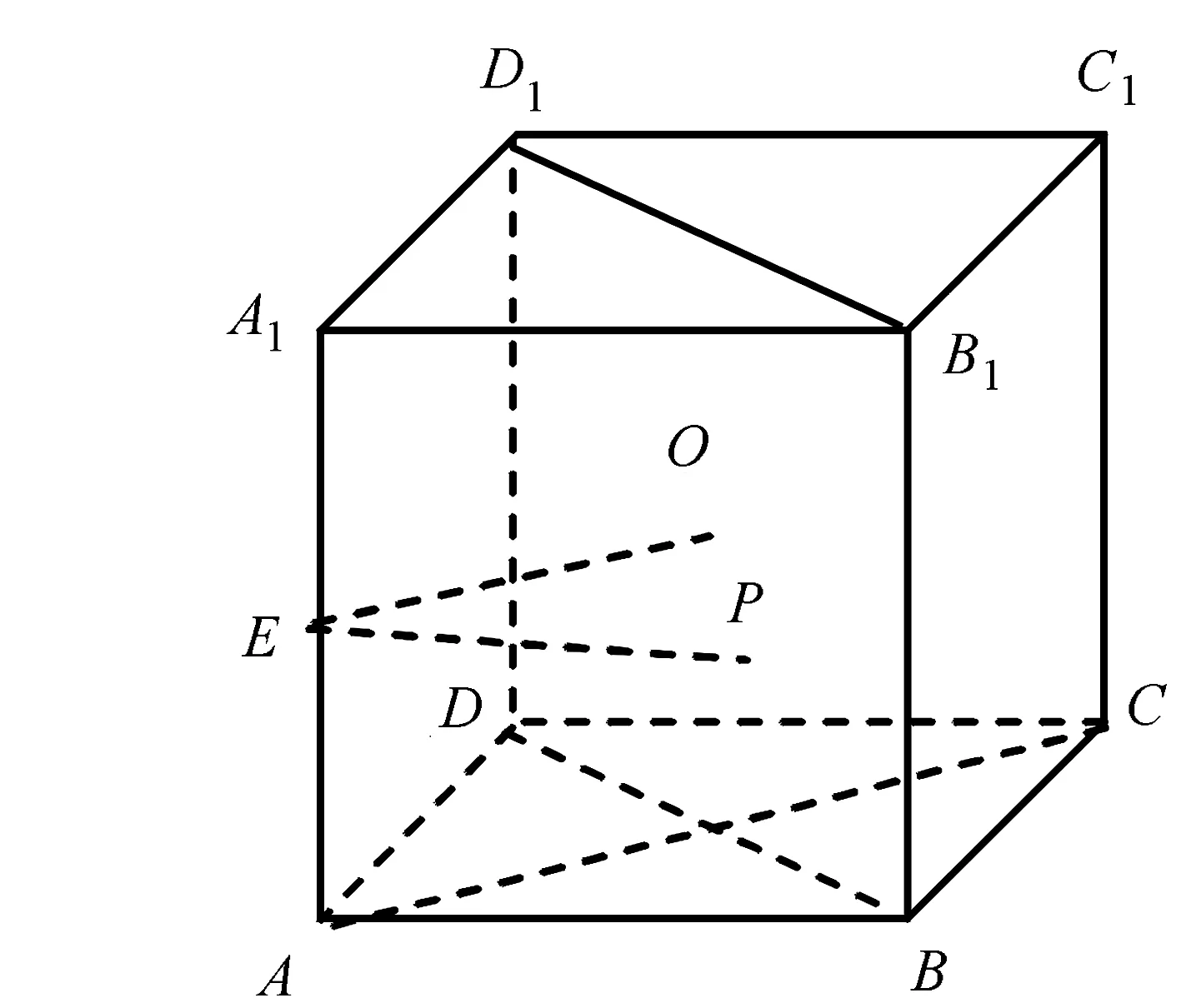
图2 例2示意图

方法1因AC是平面BB1D1D的法向量，EP总与AC成等角，所以EP与平面BB1D1D成等角，故点P到正方形BB1D1D的中心O的距离为定值，从而点P的轨迹可能是圆或圆的一部分,故选A。

方法2因为点E在对角面BB1D1D上的投影就是矩形BB1D1D的中心O, 所以AC∥EO,因此EP总与直线AC成等角等价于EP总与线段EO成等角,所以点P到矩形BB1D1D的中心O的距离为定值。所以点P的轨迹可能是圆或圆的一部分,故选A。

2 解析法

图3 例3示意图

如果轨迹问题的条件尽管是通过几何方式给出的, 但点的轨迹仅仅用立体几何、平面几何的知识很难求得，此时需要通过建立直角坐标系。

例3[4-5]在正四面体P-ABC中，M为△ABC内(含边界)一动点，且点M到3个侧面PAB、PBC、PAC的距离成等差数列，则点M的轨迹是 。

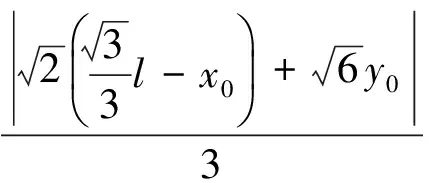
又因为M在△ABC内(含边界)，则:

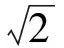
所以:

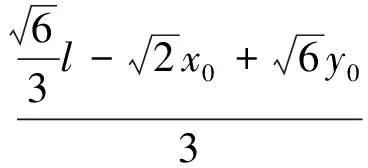
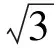
图4 正四面体P-ABC

方法2用M作为公共顶点，然后以没有M的3个面为底面可以作出3个三棱锥，这些棱锥的体积相加正好是正四面体P-ABC的体积(为常量)，而正四面体的4个面面积相等，因此3个距离和为常量。根据已知条件由于3个距离为等差数列，因此等差中项为常量。由此说明M到其中1个面的距离为常量。于是点M一定要在与这个面平行的某平面内运动,而M在四面体的一个面内，从而M的轨迹是2个面的相交线，由此一定是线段。

[1]高科军，苟玉德.空间轨迹问题的采撷[J].中学数学，2005(5)：12-16.

[2] 何天宇.由一道立体几何题的解法得到的启示[J].福建中学数学,2011(2):29-31.

[3] 夏锦. 高考题中一类定值,定点问题的求解方法[J].中学数学研究,2010(1):25-29.

[4] 王芝平. 一道高考题的多元研究[J].中学数学月刊,2008(2):41-43.

[5] 何彩萍. 例析构造法在解题中的应用[J].上海中学数学,2010(Z1):50-51.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.03.000

O182;N4

A

1673-1409(2012)03-N150-03

2011-10-15

郑剑光(1976-)，男，1999年大学毕业，中学一级教师，现主要从事数学教育方面的教学与研究工作。