隐式Runge－Kutta方法在非定常化学非平衡流动中的应用

李 芳， 刘 鑫， 尹万旺， 张 娟， 陆林生

（江南计算技术研究所，江苏 无锡214083）

0 引 言

本文研究一种适合于求解非定常化学非平衡流动的数值计算方法。该方法可应用于超声速非平衡流中的一些复杂物理现象的研究，如非定常激波／边界层相互作用、超声速边界层稳定性和转捩和超声速湍流流动等。目前普遍应用的非定常计算方法分为两大 类［1］：双时间步方法［2］（pseudo－time subiteration）和物理时间迭代方法［2］（physical time subiteration）。双时间步方法利用到两个时间：一个伪时间，另一个是物理时间；而物理时间迭代方法只利用一个时间，即物理时间。

目前应用较多的是双时间步方法。双时间步方法只需在定常程序中作少量改动即可转化为非定常程序，因此很多软件采用双时间步方法将定常程序和非定常程序合并在一起。但对于一些对时间精度要求较高的复杂非定常问题，双时间步方法暴露出两个问题：首先伪时间步迭代通常不易收敛，因而时间精度常常低于理论值2阶，有时很难反映出非定常效应，其次双时间步方法的伪时间步迭代次数较多，一般20几步，甚至50步以上，计算效率不高，计算大型复杂非定常问题耗时很长。龙格－库塔（Runge－Kutta）方法是一种精度较高的物理时间迭代方法，每个物理时间迭代中，X阶精度只需计算X步，因而计算效率较高。目前使用较多的是显式 R－K方法［7－9］，显式R－K方法时间步长小，适合求解时间分辨率很高的非定常问题，如湍流直接数值模拟。

计算非定常化学非平衡流动的主要困难在于控制方程的刚性［3－4］。由于化学反应特征时间远小于宏观非定常流动特征时间，因而化学反应非平衡源相会带来刚性。有时边界层内的细网格也会使粘性张力和热流源相带来刚性。求解刚性问题，需用隐式格式代替显式格式。目前普遍应用的隐式方法称为半隐式法，即将控制方程的刚性项和非刚性项分开，分别采用隐式和显式求解的方法。

Strang［5－6］在时间分裂方法中引入半隐式法，一部分时间推进采用隐式格式求解刚性部分，另一部分时间推进显式求解对流项，并用到上一时间步的隐式结果。这种方法消除了很多燃烧问题中遇到的隐式方法、二阶时间精度和强刚性问题的耦合，缺点是时间精度只有二阶。Bussing［7］等采用半隐式 Mac－Cormach法计算可压缩化学反应流，化学反应项隐式，流动项显式。Engquist和Sjogreen［8］采用 TVD格式和ENO格式离散对流项，采用半隐式法将源相合并到Runge－Kutta时间推进中求解了爆炸波。Zhong［9－11］以泰勒展开为基础，非刚性项显式处理，刚性项隐式处理，推导了一种满足高精度和强稳定性条件的半隐式Runge－Kutta方法，但这种方法系数繁多，计算过程比较复杂。

本文提出一种新的隐式Runge－Kutta方法，中间步的系数与经典显式Runge－Kutta方法相同，隐式体现在右端项的计算。这种隐式R－K的方法的时间精度和同阶显式R－K方法相当，时间步长可以取的较大，因而计算效率较高，同时计算公式简单，实现方便，可以很容易地从定常程序转化为非定常程序。

1 求解NS方程组的隐式龙格－库塔法

计算坐标系下，三维非定常化学反应非平衡流动的无量纲NS方程为：

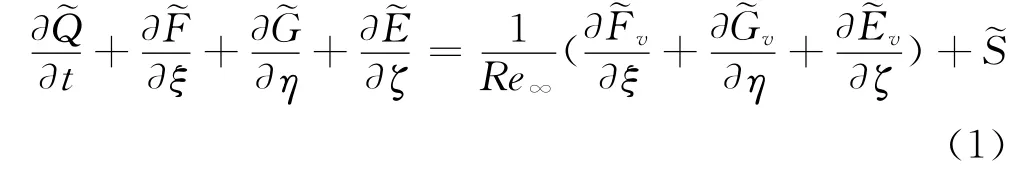
R－K法本是求解常微分方程的一类高精度方法，为在偏微分方程（1）中应用R－K法，需将方程（1）变为如下形成：

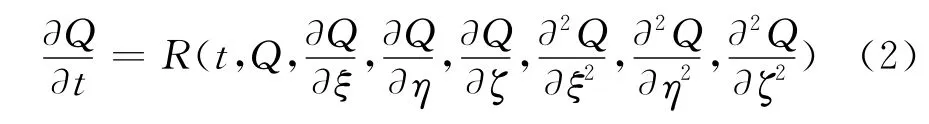
采用隐式方法，需分别对无粘对流项、粘性项和源项进行线化处理，线化方法与定常程序类似，对流项采用Jacobian矩阵分裂法线化，粘性项采用近似特征值法线化，源项采用对角化法线化［12］，线化后方程（2）的右端项可表示为：

式中，α＝0为空间显式格式，α＝1为空间隐式格式；βD＝0时，化学源项不做隐式线化，βD≠0时，化学源项隐式线化；ρ（）、ρ（）、ρ（）分别为矩阵、、的谱半径

采用δQ的形式，2阶精度隐式R－K法可表示为：

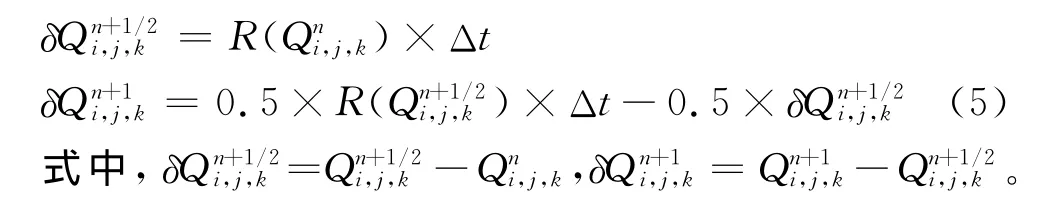
采用δQ的形式，3阶精度隐式R－K法可表示为：

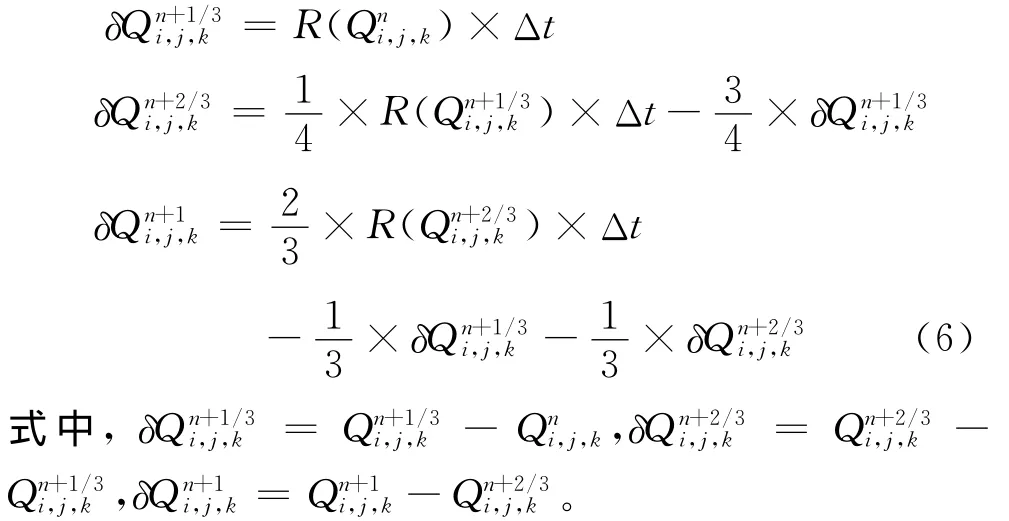
由于采用相同的线化方法，因此隐式R－K方法的右端项计算方法与定常程序相同，可以方便地从定常程序转化为非定常程序。

2 算例计算结果与分析

2.1 隐式R－K方法正确性验证

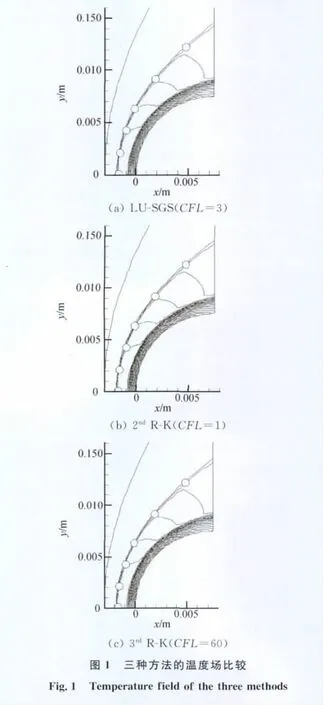
为验证算法正确性，选取了六个典型定常算例：湍流平板、二维燃烧室、超声速压缩拐角、三维进气道、球头激波诱导燃烧、非对称交叉激波。分别采用隐式LU－SGS方法［13］和2阶、3阶隐式 R－K方法进行数值模拟，并将计算结果与实验结果进行比较，结果表明三种隐式方法计算结果一致，且与试验吻合。由于篇幅有限，这里仅给出球头激波诱导燃烧计算5000步时的温度场，如图1所示。从图中可看出，计算5000步时，三种时间推进方法的温度场均已收敛，激波形状几乎完全相同，与试验值吻合；3阶隐式RK法的CFL数可取到60，2阶隐式R－K法和隐式LU－SGS方法的CFL数较小，可见3阶隐式R－K法稳定性较好。

2.2 隐式R－K方法在非定常问题中的效率

非定常问题极其复杂，且计算量巨大，即使采用成千上万个CPU并行计算，模拟一个大型实际问题也需要几天甚至十几天时间，因此求解非定常问题，除了考虑数值格式的稳定性和精度以外，计算效率也非常重要。

20世纪60～70年代，Lehr［14］通过试验发现球头激波诱导燃烧存在非定常现象，之后Jeong［15］等针对该现象开展了数值模拟研究，并取得较满意的结果。由于化学反应非常快，并且在很短的距离内伴随着大量能量释放，因此对数值格式的健壮性和精度要求较高。本文通过对球头激波点火试验进行数值模拟来校验隐式R－K方法模拟非定常现象的精度和效率。

来流条件为马赫数4.48，压强42663.16Pa，温度293K，来流质量分数为CH2＝0.0283，CO2＝0.227，CN2＝0.74507。计算采用二维轴对称欧拉方程，无粘通量采用S－W分裂，化学反应为9组分19方程的反应模型，使用256个CPU并行计算。

时间推进分别采用2阶隐式、3阶隐式R－K法和2阶双时间步方法（伪时间迭代为20步），当时间步长均为10－9s时，点火过程中驻点压强随时间的变化曲线如图2所示。可以看出，三种方法的驻点压强均在点火后出现了一定频率的振荡，表明流场中产生了爆轰波现象，与实验结果吻合。三种方法的振荡频率和振幅接近，均能正确描述该非定常问题。

采用不同的时间步长，3阶隐式R－K法和2阶双时间步方法得到的振荡频率如表1所示。从表1可看出，随着时间步长的缩小，两种方法得到的振荡频率均增加，并逐渐靠近参考值：426kHz［15］。

表1 不同时间步长得到的振荡频率（kHz）Table 1 Vibration frequency with different time step（unit：kHz）

2阶隐式、3阶隐式R－K法和2阶双时间步方法均为空间导数离散的隐式格式，时间步长可以取得相当。一个物理时间步长内，2阶隐式R－K法计算2次，3阶隐式R－K法计算3次，双时间步方法计算20（伪时间迭代数）次，因此取相同的物理步长和总计算步数，双时间步方法的总计算时间分别为2阶、3阶R－K方法的10倍和6.67倍，由此可见，隐式R－K方法在计算效率方面有绝对优势。

3 结 论

本文以经典的显式Runge－Kutta方法为基础，推导了一种求解NS方程组的隐式R－K方法。该方法通过右端项隐式处理，解决了化学反应非平衡流动带来的刚性问题，同时计算公式简单，实现方便，可以很容易地从定常程序转化为非定常程序。最后通过定常算例和非定常算例对隐式R－K方法进行了验算，分析表明该方法计算结果正确，精度较高；能够正确求解复杂非定常化学反应非平衡流动，且算法健壮性好、精度高、效率高。

致谢：衷心感谢中国空气动力研究与发展中心杨顺华博士、赵慧勇博士和王西耀博士提供的测试算例，以及对计算结果的分析与处理。

［1］RUMSEY C L，SANETRIK M D，BIEDRON R T，et al.Efficiency and accuracy of time－accurate turbulent Navier－Stokes compuations［R］.AIAA paper 95－1835，1995.

［2］PULLIAM T H，Time accuracy and the use of implicit methods［R］.AIAA paper 93－3360，1993.

［3］ZHONG X.Direct numerical simulation of hypersonic boundary layer transition over blunt leading edges，Part I：a new numerical method and validation［R］.AIAA Paper 97－0755，1997.

［4］ZHONG X.Direct numerical simulation of hypersonic boundary layer transition over blunt leading edges，Part II：receptivity to sound［R］.AIAA Paper 97－0756，1997.

［5］STRANG G.On the construction and comparison of difference schemes［J］.SIAMJournalofNumerical Analysis，1968，5：506－517.

［6］LEVEQUE R J，YEE H C.A study of numerical methods for hyperbolic conservation laws with stiff source terms［J］.JournalofComputationalPhysics，1990，68：187－210.

［7］BUSSING T R A，MURMAN E M.A finite volume method for the calculation of compressible chemically reacting flows［R］.AIAA Paper 85－0296，1985.

［8］ENQUIST B，SJOGREEN B.Robust difference approximations of stiff inviscid detonation waves［R］.Report 91－03，CAM，Department of Mathematics，University of California，1991.

［9］ZHONG X.Additive semi－implicit Runge－Kutta methods for computing high－speed nonequilibrium reactive flows［J］.JournalofComputationalPhysics，1996，128：19－31.

［10］JACK JAI－ICK YOH.ZHONG X.Low－storage semiimplicit Runge－Kutta methods for reactive flow computations［R］.AIAA Paper 98－0130，1998.

［11］ZHONG X.New high－order semi－implicit Runge－Kutta Schemes for computing transient nonequilibrium hypersonic flow［R］.AIAA Paper 95－2007，1995.

［12］赵惠勇.超燃冲压整体发动机并行数值研究［D］.四川绵阳：中国空气动力研究与发展中心，2005.

［13］JAMESON A，YOON S.LU implicit scheme with multiple grid for the Euler equations［R］.AIAA paper 86－0105，1986.

［14］LEHR H F.Experimenta on shock－induced combustion［J］.AstronauticaActa，1972，17（4－5）：195－203.

［15］CHOI J Y，IN－SEUCK JEUNG，YOUNGBIN YOON.Computational fluid dynamics algorithms for unsteady shock－induced combustion，Part I：validation ［R］.AIAA paper 98－3217.