斜切式洞门缓冲结构开口率的优化分析

2012-11-09贺旭洲王英学付业凡彭永利

空气动力学学报 2012年2期

贺旭洲，王英学，付业凡，彭永利

（1.湖北省交通规划设计院，湖北武汉430051；2.西南交通大学土木工程学院，四川成都610031）

0 引言

随着高速铁路的发展，列车速度不断提高，高速列车在隧道内运行的空气动力学问题也日益突出。当高速列车头部进入隧道时，由于受到地形条件的影响，因而在隧道入口处产生压缩波，压缩波沿着隧道向前以声速传播并产生变形。在隧道出口处由于隧道断面面积突然发生急剧的变化，传播到此处的压缩波，大部分能量向隧道内以膨胀波的形式反射回去，造成隧道内压力波动，影响乘车舒适度；同时将向外辐射出一低频脉冲波，即微气压波，在隧道出口产生声爆现象，从而对周围环境造成较严重危害［1］。

国内外研究表明，该脉冲波的最大值与压缩波到达隧道出口的最大压力梯度成正比［2］，而减小压缩波在隧道入口产生的最大压力梯度，通常可以减小压缩波到达隧道出口时的最大压力梯度，从而减缓声爆现象；同时，隧道内产生的压力波动也与隧道入口产生的初始压缩波密切相关。

降低压缩波在隧道入口产生的最大压力梯度的措施主要包括在隧道内设置支洞、竖井、优化列车头部形状、在隧道入口处增设缓冲设施［3］等。本文应用三维数值模拟方法来模拟高速铁路列车单车突入顶部开口的斜切式洞门隧道时的压力变化情况，研究高速铁路隧道斜切式洞门顶部开口面积大小对压力峰值、压力梯度降低效果的影响。

1 气动效应数值分析中的动网格理论

列车在进出隧道过程中，边界条件是变化的。为了实现这一过程，在计算中可以采用滑移网格技术，也可以采用动网格模型来模拟流场边界随时间改变的问题。动网格的基本理论如下：

在任意一个控制体中，广义标量φ的积分形式守恒方程为：

式中，ρ为流体密度，u为速度向量，ug移动网格的网格密度，Γ为扩散系数，Sφ为源项，∂V代表控制体V的边界。

方程（1）中的时间导数项，可以用一阶向后差分格式写成：

式中n和n＋1代表不同的时间层。n＋1层上的Vn＋1由下式计算：

为了满足网格守恒定律，控制体的时间导数由下式计算：

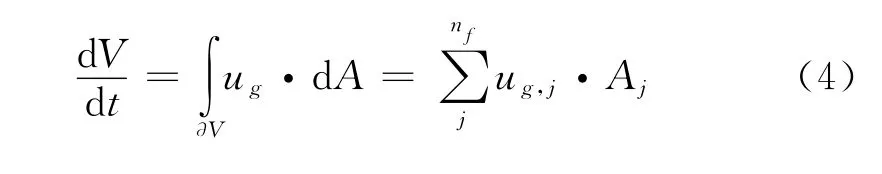
式中nf是控制体的面网格数，Aj为面j的面积向量。

点乘ug，j·Aj由下式计算：

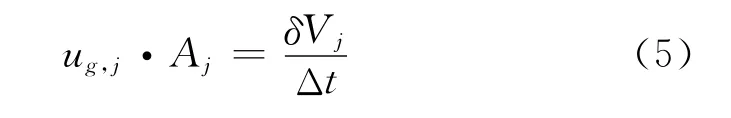
式中δVj为控制体积面j在时间间隔Δt中扫过的空间体积。

将方程中广义标量φ应用于质量、动量、能量方程。同时，注意到，计算中采用理想气体作为介质，就可以求解出在动网格模型时的流场状态。动网格计算方法有弹簧光顺法、动态层技术和局部网格重划法3种。本文动网格计算方法采用动态层技术。

2 计算实例

在数值计算中，假设空气是有粘性、可压缩、理想气体，紊流方程采用标准k－ε模型。数值计算中取隧道长度L＝978m（这里不考虑隧道长度对于压缩波的非线性效应），列车（CRH3型）长度L＝100m，列车横断面积为11.624m2，列车速度分别为250km／h、300km／h和350km／h，隧道横断面积为100m2，隧道阻塞比σt（σt＝A0／A，A0为列车横断面积，A为隧道横断面积）为0.116。斜切式洞门，伸出洞门长度为15m（考虑到斜切式洞门的顶部与底部长度不同，因此按洞门的顶部计长度），两侧为斜切，边墙比率1∶1，顶部开双口，开口率（洞口顶部双口面积与隧道常规段断面积之比）取21.8%、25%、30%三种情况，具体见表1所示。隧道入口处的斜切式洞门缓冲结构网格划分如图1所示。

图1 顶部开口的斜切式洞门Fig.1 Bamboo－truncating portal with top openings

表1 数值计算工况Table 1 Numeral calculation conditions

3 计算结果与分析

ORE的研究报告表明，列车在隧道中运行时（无相向行驶列车）车上测得的最大压力波动发生在第一个反射波到达列车时［4］。因此，笔者主要研究首波特性。选取距隧道入口200m处的测点，通过考察首波压力峰值和压力梯度峰值，来研究高速铁路隧道斜切式洞门缓冲结构开口率的大小对空气动力学效应的影响。

隧道洞口无缓冲结构与设置斜切式洞门缓冲结构时，测点处的首波压力峰值及压力梯度统计如表2和表3所示。

表2 测点处首波压力峰值Table 2 First－wave peak－pressure at measuring point

由图2可以看出：在设置斜切式洞门缓冲结构后，同一速度下首波压力峰值随开口率的增加无明显的变化，与无缓冲结构相比，首波压力峰值的降低效果不明显。这与王英学等降低气动效应综合措施的试验研究得到的结论一致：洞口缓冲设施降低首波压力峰值的效果不明显［5］。

图3显示了无缓冲及斜切式洞门缓冲结构在三种开口率下测点处的压力梯度值。从图3中可以看出，设置斜切式洞门缓冲结构后，压力梯度得到了明显的降低；速度为250km／h时，开口率对压力梯度的影响相差不大，速度300km／h时，压力梯度随开口率的不同有较大的波动。

表3 测点处压力梯度及降低率Table 3 The pressure－gradient and reduction ratio at measuring point

图4、图5分别显示了在设置斜切式洞门缓冲结构与无缓冲结构时相比，压力梯度降低率与开口率、速度之间的关系。由图4可以看出，列车以低速（250km／h）突入隧道时，压力梯度降低率随开口率的增加而增大；列车以高速（350km／h）突入隧道时，压力梯度降低率随开口率的增加，出现先增大后减小的现象，因此存在一最优开口率，且最优开口率为25%。针对列车以250km／h和300km／h的速度突入隧道时，压力梯度曲线没有出现明显的峰值点，可能与隧道长和列车长之比、斜切式洞门边墙比率、阻塞比等有关，这点需要作进一步的研究。

图4 测点处压力梯度降低率随开口率而发生变化Fig.4 The ratio of maximum pressure gradient with different aperture ratios at measuring point

由图5可以看出，当列车以250km／h的速度突入隧道时，不同开口率下的降低效率相差不大，开口率为30%时降低效果较好，压力梯度降低率达到49%；当列车以300km／h的速度突入隧道时，开口率为21.8%时降低效果较好，压力梯度降低率达到30%；当列车以350km／h的速度突入隧道时，开口率为25%时降低效率最优，压力梯度降低率达到32%。