基于激励盘理论的螺旋桨滑流数值模拟研究
2012-11-09夏贞锋
夏贞锋, 罗 淞, 杨 永
(西北工业大学 翼型叶栅空气动力学国防科技重点实验室,陕西 西安710072)
0 引 言
螺旋桨发动机在飞机低速飞行时具有拉力大、推进效率高、经济性好等特点,在运输机领域发挥着不可替代的作用。但是,螺旋桨的旋转运动,使其周围流动变得非常复杂,特别是螺旋桨滑流与飞机气动部件之间的干扰现象,对数值模拟提出了很高的要求。
目前,模拟螺旋桨滑流的数值方法主要有两种:一是对该非定常流场直接进行数值模拟[1-2];另一种是建立激励盘模型[2-4],用无厚度的激励盘代替螺旋桨的作用。尽管非定常流场数值模拟方法能够捕捉复杂桨尖涡等流动现象,但是,网格生成的难度和模拟时间的要求大大增加了计算成本。相比之下,采用激励盘理论,几何模型的简化显著降低了网格生成的难度,同时,对流场的定常模拟方式也大大缩短了计算时间。因此,在研究螺旋桨滑流影响的工程应用中,激励盘模型具有更大的优势。
激励盘载荷分布决定着激励盘模型能否准确地模拟螺旋桨滑流。通常,激励盘载荷分布是根据经验公式[3,5]或叶素理论[6]确定的,与实际螺旋桨载荷有一定的偏差,使得激励盘理论模拟的滑流精度不够高。
本文采用非定常方法模拟单独旋转螺旋桨流场得到桨叶载荷分布,从而确定激励盘载荷,建立激励盘模型。并对激励盘旋向载荷分布对滑流模拟的影响进行了研究,对比分析该激励盘模型对滑流的模拟精度。
1 激励盘模型
激励盘理论根据通过螺旋桨的气流动量变化,将螺旋桨近似成一个无厚度圆盘。螺旋桨桨叶不仅受到轴向的拉力还受到气流的旋向阻力,在建立激励盘模型时需要考虑这两个方向的载荷分布。根据动量定理,激励盘前后的压力增量产生拉力载荷,气流的旋向动量变化量产生旋(周)向载荷。最终,激励盘载荷分布以压强增量和旋转速度增量形式给出。
本文激励盘的载荷分布是通过对单独旋转螺旋桨流场进行非定常模拟得到的。桨叶载荷具有非定常的周期性,激励盘载荷则是不随时间变化的,所以需要确立一个周期内载荷分布的对应关系。桨叶旋转微元与激励盘微元如图1、图2所示。
桨叶径向r处的拉力T′和周向力在径向微元dr上不变,作用时间为桨叶旋转过dθ角度的时间dt=dθ/ω,其中ω为旋转角速度。
在dt时间内,桨叶微元dr扫过的面积为

通过面积dS的气流轴向动量变化量dIt和旋向动量变化量dIθ分别为

螺旋桨旋转一个周期的时间为T=2π/ω。在一个周期的其它时间,即T-dt时间内,通过面积dS的气流动量变化量为零。因此,一个周期T时间内,单个桨叶引起的通过面积dS的气流轴向和旋向动量变化量分别为dIt和dIθ。若桨叶数为N,那么一个周期T时间内通过面积dS的气流轴向和旋向动量变化量分别为N·dIt和N·dIθ。
激励盘压强增量Δp和旋转速度增量Δvθ在面积dS上均匀分布,作用时间为一个周期T。那么一个周期T时间内,通过面积dS的气流轴向和旋向动量变化分别为Δp·dS·T和Δvθ·(ρu)·dS·T,其中ρ和u分别为激励盘处气流的密度和速度。
因此,螺旋桨桨叶与激励盘在轴向和旋向的载荷分布对应关系分别为



2 数值模拟方法
2.1 非定常模拟方法
积分形式的三维Navier-Stokes控制方程为

其中Q=[ρ,ρu,ρv,ρw,et]T,F为粘性和无粘通量矢量,Ω为控制体,∂Ω为控制体边界,n为∂Ω的外法线方向单位矢量。由于流场数值模拟基于惯性坐标系,式(3)不含非惯性项。
采用有限体积法离散上述控制方程。无粘通量项采用二阶精度的Roe通量差分分裂迎风格式离散,粘性通量项采用二阶中心差分格式离散。采用全湍流假设,Spalart-Allmaras湍流模型进行湍流计算。采用双时间方法进行时间推进,在子迭代中采用多重网格、当地时间步长等加速收敛措施。
2.2 激励盘模拟方法
控制方程及空间离散格式同上述的非定常模拟方法。采用隐式时间推进,并采用多重网格、当地时间步长等措施加速收敛。采用文献[5]的方法,把激励盘前后的压强增量和旋转速度增量作为边界条件加入到求解程序中,实现激励盘理论对滑流的模拟。
3 算例及分析
3.1 单独旋转螺旋桨流动模拟
采用非定常数值模拟方法对单独螺旋桨旋转时的流场进行模拟,从而得到桨叶载荷分布,模型如图3所示。网格为多块点点对接网格,共270块。为了捕捉桨尖涡的发展过程,对螺旋桨后空间网格进行加密,网格量为6.2E06。数值计算时,整体网格随螺旋桨以同一角速度旋转。螺旋桨的旋转角速度固定为ω=1075rad/min,前进比λ=1.1时,对应的远场来流马赫数Ma=0.2319,雷诺数Re=5.4×106,来流攻角α=0°。

图3 螺旋桨模型及网格Fig.3 Propeller model and grid
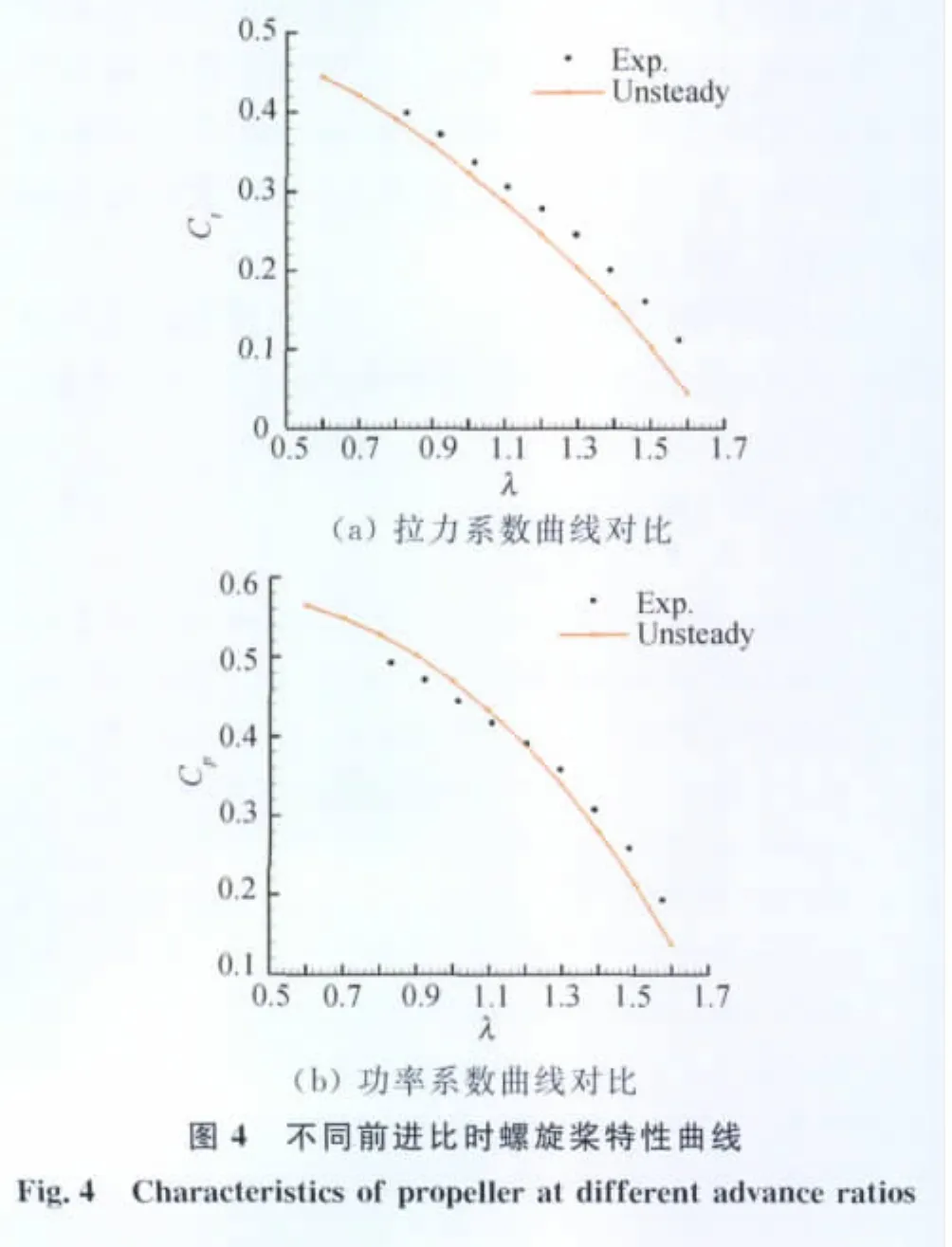
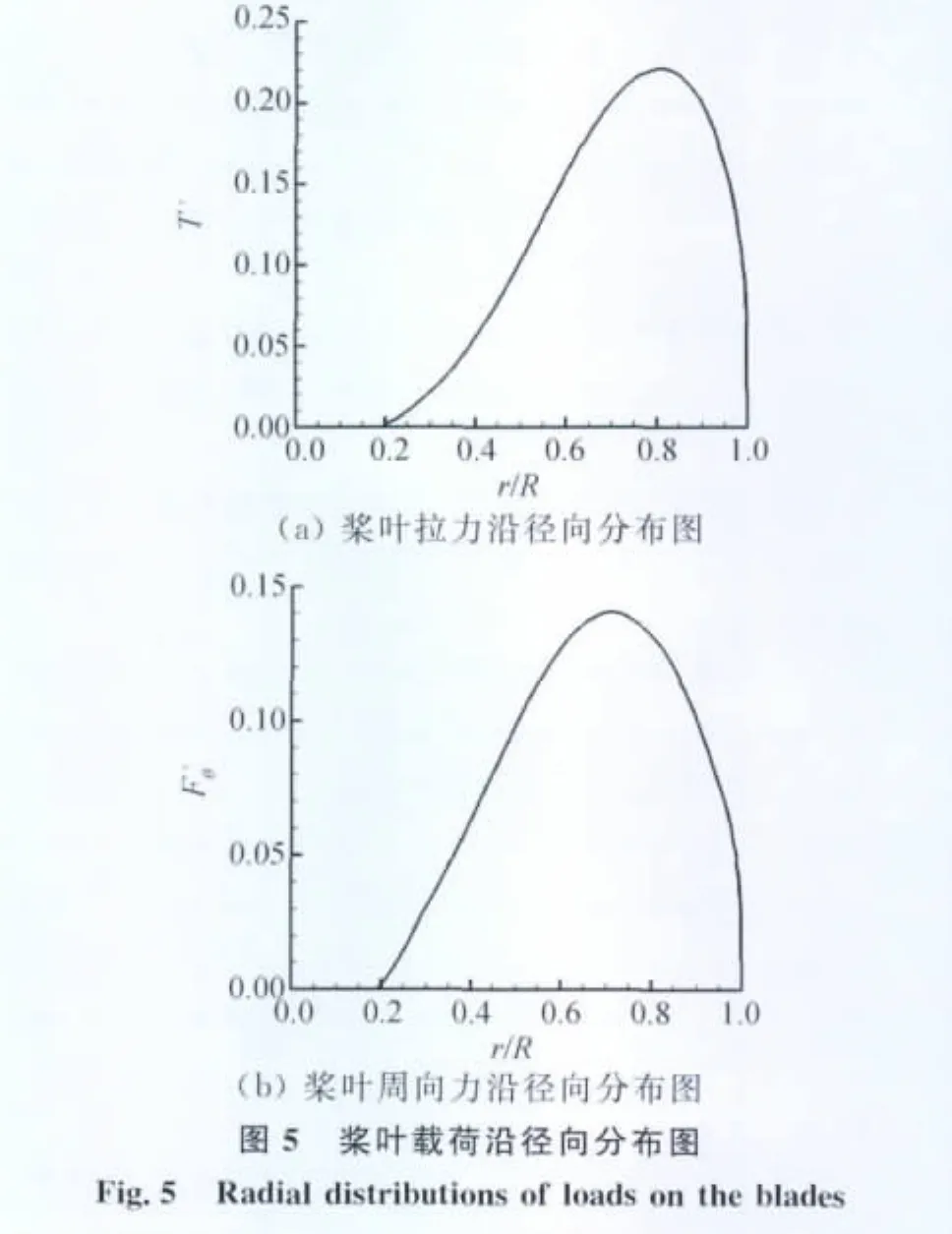
在不同前进比状态下,非定常数值模拟得到的螺旋桨拉力和功率特性与实验值的比较如图4(a、b)所示。可以看出,随着前进比λ的增大,拉力系数Ct和功率系数Cp均减小,与实验结果吻合较好。以前进比λ=1.1为例,非定常数值模拟得到的螺旋桨拉力系数为0.2860,和实验值0.3057相差6.4%,功率系数为0.4330,与实验值0.4177的偏差为3.7%。可以说,非定常数值模拟方法比较准确地模拟出螺旋桨的力与力矩特性。来流攻角α=0°时,理论上各个桨叶的载荷分布不随时间变化。图5(a、b)分别为前进比λ=1.1时无量纲的桨叶总拉力T′和总周向力沿径向的分布。图5(a)中显示的最大拉力在桨叶半径的80%附近,图5(b)中则给出最大周向力在桨叶半径的70%到75%之间,与螺旋桨的特性一致。因此,可以将该非定常模拟结果应用于激励盘理论模拟滑流的比较。
3.2 激励盘理论滑流模拟
采用激励盘理论模拟滑流的模型见图6,取螺旋桨旋转平面作为激励盘。网格为多块点点对接网格,共44块,网格量为3.5×106。网格生成比图3所示的螺旋桨网格简单很多。来流攻角α=0°时,激励盘载荷在圆环内均匀分布。根据式(1、2),分别由图5(a、b)的桨叶拉力和周向力分布得到图7(a、b)的激励盘压强增量Δp分布和旋转速度增量Δvθ分布。

图6 激励盘几何模型及网格Fig.6 Actuator disk model and grid
分别对只考虑轴向载荷作用的激励盘和同时考虑旋向载荷的激励盘进行滑流模拟。图8给出了两种激励盘模型的模拟结果与非定常模拟旋转螺旋桨的时间平均流场的比较。图8(a、b)分别为桨盘后x/R=1.73处滑流中轴向速度分布和周向速度分布。图8(a、b)中的点画线显示出只加入压强增量的激励盘的模拟结果。从图8(a)中对比可以看出,同时考虑旋转速度增量Δvθ时轴向速度分布更接近非定常时均结果。只考虑Δp时,通过激励盘气流不发生旋转,即滑流的周向速度为零,见图8(b)。从图8(a、b)中实线与虚线的对比可以看出,同时考虑压强增量Δp和旋转速度增量Δvθ时,滑流的轴向速度和周向速度分布与非定常计算的时均结果在大部分区域内一致,只在桨尖和桨根后有些微的差异。这些差异主要是因为激励盘理论采用定常方式模拟流场,无法模拟桨尖涡及桨根涡等局部流动细节。综上所述,同时加上轴向载荷和旋向载荷分布的激励盘模型可以更准确地模拟螺旋桨滑流。


4 结 论
本文的数值模拟结果表明,在激励盘模型中,加入旋向载荷分布,能够实现对激励盘后气流旋转的模拟,更准确地模拟螺旋桨滑流;与非定常数值模拟方法相比,采用本文的激励盘模型,能够在保证足够的精度的条件下,降低网格生成难度,显著缩短数值模拟所需的CPU时间。
因此,在模拟螺旋桨动力飞机气动特性的工程应用中,该激励盘模型比非定常模拟方法有更大的优势。
[1]STUERMER A.Unsteady Euler and Navier-Stokes simulations of propellers with the unstrucutred DLR TAU-code[A].RATH H J,HOLZE C,et al.New Results in Numerical and Experimental Fluid Mechanics V[C].Springer,2006.144-151.
[2]KHIER W.Time-accurate versus actuator disk simulations of complete helicopters[A].NAGEL W E,RESCH M,WJÄGER.High Performance Computing in Science and Engineering'05[C].Springer,2006.209-220.
[3]李博,梁德旺,黄国平.基于等效盘模型的滑流对涡桨飞机气动性能的影响[J].航空学报,2008,29(4):845-852.(LI B,LIANG D W,HUANG G P.Propeller slipstream effects on aerodynamic performance of turboprop airplane based on equivalent actuator disk model[J].ChineseJournalofAeronautics,2008,29(4):845-852.)
[4]CHUITON F L.Actuator disk modelling for helicopter rotors[J].AerospaceScienceandTechnology,2004,8:285-297.
[5]左岁寒,杨永.螺旋桨滑流对带后缘襟翼机翼气动特性影响的数值分析[J].航空计算技术,2007,37(1):54-57.(ZUO S H,YANG Y.Numerical simulation of propeller/high-lift system interaction[J].AeronauticalComputingTechnique,2007,37(1):54-57.)
[6]RAICHLE A,WILKENDING S M,HIMISCH J.A new actuator disk model for the TAU code and application to a sailplane with a folding engine[A].TROPEA C,JAKIRLIC S,HENKE R,et al.New Results in Numerical and Experimental Fluid Mechanics VI[C].Springer,2008:52-61.
