轴压和不均匀内压下钢筒仓圆柱壳屈曲承载力研究
2020-01-02张翀舒赣平
张翀 舒赣平
(1.东南大学建筑设计研究院有限公司 南京210096;2.东南大学土木工程学院 南京210096)
引言
钢筒仓的仓壁为圆柱薄壳结构,仓内储料对仓壁的内压和轴压是钢筒仓所承受的主要荷载,理论和实验研究表明,一定量级以内的对称均匀的内压对仓壁的屈曲承载力有一定的提高作用。但钢筒仓在实际使用中,更多的处于储料分布不均匀以及偏心卸料所造成的不均匀内压的作用下。对于轴压和不均匀内压下仓壁的受力性能研究较少,目前主要集中在以下几个方面:文献[1]对钢筒仓的仓壁在轴压和均匀内压的共同作用下的屈曲承载力进行了研究,得到了相关计算公式;文献[3]~[5]对局部轴压以及局部轴压与均匀内压共同作用下钢筒仓的屈曲性能进行了研究,得到了相关计算方法;文献[6]~[9]对目前钢筒仓研究方面存在的问题进行了综述,对比了中国规范和欧洲规范中有关钢筒仓稳定设计的方法,这些文献均指出了《粮食钢板筒仓设计规范》(GB50322-2001)[10]在钢筒仓稳定设计中某些方面的缺失,诸如规范中并未包括轴压和不均匀内压共同作用下钢筒仓仓壁的屈曲承载力的计算方法。
本文主要针对以上情况,在文献[1]的基础上,对轴压和不均匀内压共同作用下仓壁的屈曲承载力进行了研究。为了得到钢筒仓仓壁屈曲承载力的统一的表达形式,文献[1]引入了轴压圆柱壳体的经典屈曲临界应力σx,Rcr,把钢筒仓仓壁在各种荷载作用下的屈曲承载力σcr写成折减系数乘以经典屈曲临界应力的形式,如式(1)所示。
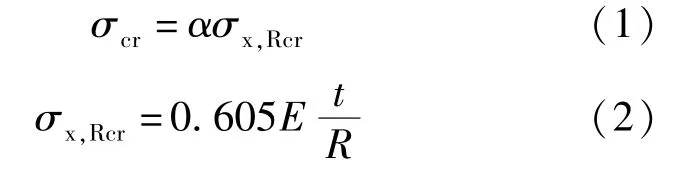
式中:E为钢材的弹性模量(MPa);t为仓壁钢板厚度(m);R为钢筒仓圆柱壳的半径(m);α为各种荷载工况下的折减系数,该折减系数分为如下几种情况:仅轴压下的弹性折减系数α0,轴压与均匀内压共同作用下的弹性和弹塑性折减系数αpe和αpp,其中α0和αpe在《粮食钢板筒仓设计规范》(GB50322-2001)[10]中给出,αpp在文献[1]中给出。本文通过计算分析,给出轴压和不均匀内压共同作用下,仓壁的弹性和弹塑性屈曲承载力的折减系数αecc,e和αecc,p,对规范中筒仓临界屈曲应力的规定进行补充和完善。
1 计算模型的建立
在文献[1]中所采用的计算模型的基础上,引入了6 种非均匀内压,这6 种不均匀内压主要由6 种不同的卸料口直径和卸料口的偏心状态导致(如表1中所示),具体可按文献[2]中的方法计算,其中一种不均匀内压形式如图1所示。参考均匀内压的无量纲内压定义,取高度为0、圆周角度为180°处的内压值Pl0为基准,定义不均匀内压的无量纲内压值如式(3)所示。
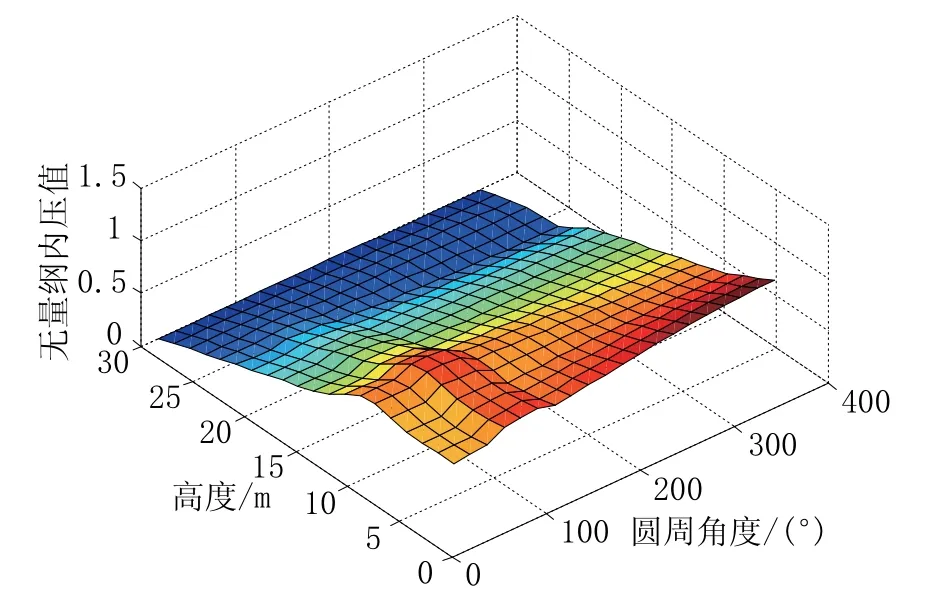
图1 一种不均匀内压分布Fig.1 One distribution of non-uniform inner pressure

在ABAQUS 中建立有限元模型,采用s4 壳单元,进行轴压和不均匀内压共同作用下钢筒仓仓壁的屈曲承载力的参数化有限元分析,各种计算模型的参数如表1所示。考虑的4 种初始缺陷模型与文献[1]中一致。
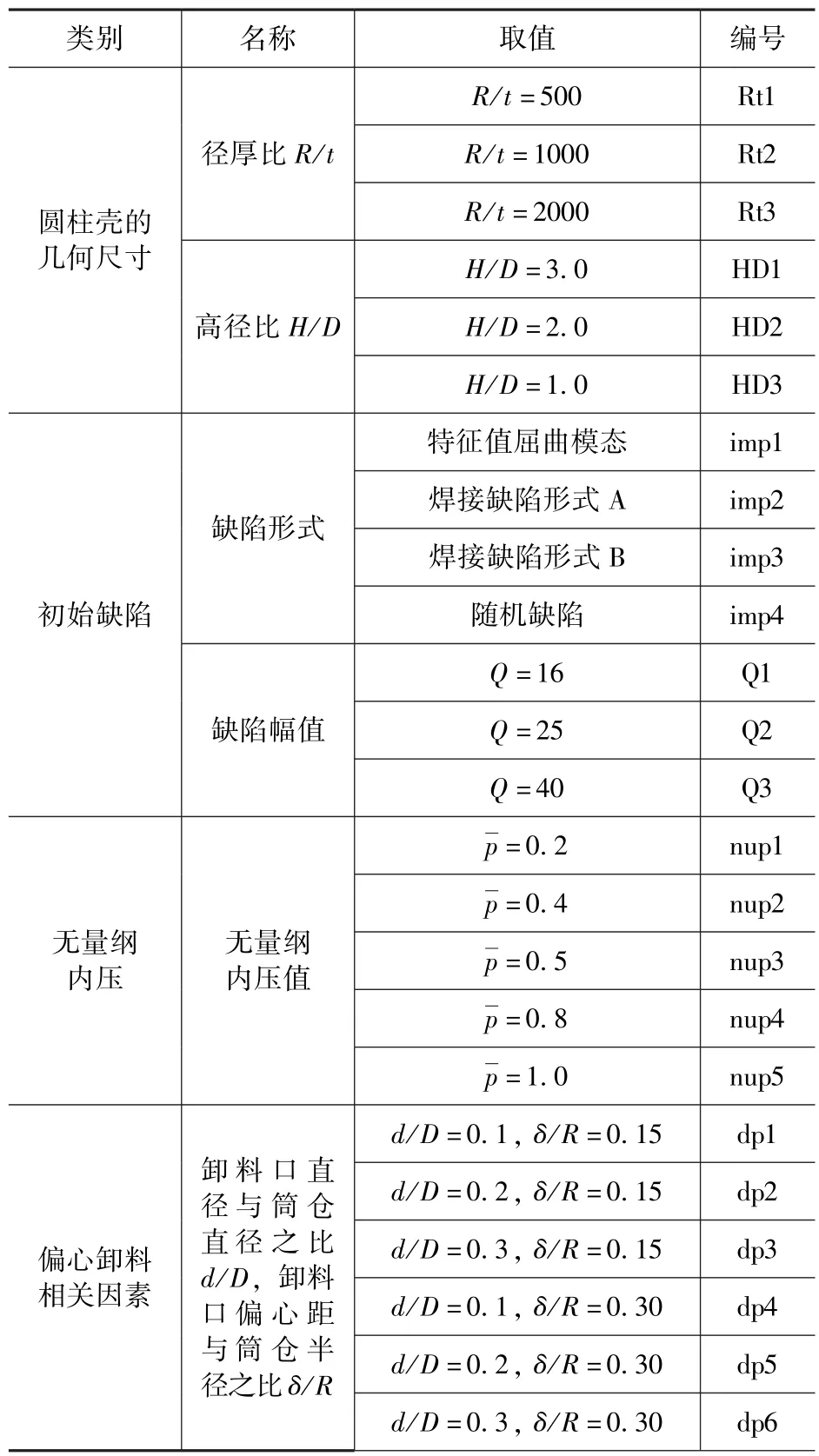
表1 计算模型参数化分析取值Tab.1 The value of parameter in analysis model
2 不均匀内压和轴压下屈曲承载力分析
为了研究轴压和不均匀内压共同作用下仓壁屈曲,选取了一种计算模型进行研究,该模型的几何参数为:H=20.0m、D=10.0m、t=0.005m,高径比H/D=2.0、径厚比R/t=1000,考虑了4 种初始缺陷、缺陷幅值为Q=16,3 种无量纲内压值,分别为=0.2、0.5、1.0,以及6 种偏心卸料工况。加载时,首先施加不均匀内压,再施加均匀轴压直至达到屈曲承载力。
2.1 弹性屈曲承载力分析
1.四种缺陷形式的影响
首先考察了4 种缺陷形式对屈曲承载力的影响,表2给出了该模型4 种缺陷形式在轴压和无量纲内压值为0.2 的不均匀内压(对应偏心卸料工况dp1)下的弹性无量纲临界应力。从表中可见,一阶特征值屈曲模态缺陷的临界应力最高,焊接缺陷A 的临界应力最低,焊接缺陷B 的临界应力与焊接缺陷A 的临界应力接近,而随机缺陷的临界应力介于一阶特征值屈曲模态缺陷与焊接缺陷之间。

表2 四种缺陷筒壳的无量纲弹性临界应力Tab.2 The relative elastic critical stress of shells with four kinds of imperfections
图2给出了不均匀内压施加完毕后的变形,图中显示筒壳出现了局部的凸起(筒壳向外的变形)和凹陷(筒壳向内的变形),造成筒壳局部凸起的是圆周方向上叠加的局部侧压力,在叠加局部侧压力处筒壳产生了局部凸起,在其两侧相邻位置处产生了局部凹陷,从δ/R=0.15、d/D=0.1m 的偏心卸料状况所对应的不均匀内压值来看,一处局部凹陷的位置位于卸料口中轴线上靠近偏心卸料口处(下文简称右侧凹陷),一处位于与卸料口中轴线成90°夹角处(下文简称左侧凹陷)。这种由不均匀内压造成的筒壳的前期变形,是筒壳在施加轴压后产生屈曲的主要原因,这一点可由施加轴压后筒壳在达到临界应力时的变形图看出。

图2 四种缺陷筒壳在不均匀内压施加完毕后的变形Fig.2 The deformation of shells under non-uniform pressure with four kinds of imperfections
筒壳在达到临界应力后的变形如图3所示,其前期不均匀内压造成的局部凸起和凹陷量继续增大,一阶特征值屈曲模态缺陷的筒壳的左侧凹陷量显著增大,焊接缺陷A 的筒壳其焊接缺陷原本就在筒壳中部形成一环形内凹区域,不均匀内压形成的左、右两侧凹陷区域的焊接凹陷进一步增大,轴压又进一步加大了凹陷程度,焊接缺陷B 的筒壳左、右两侧凹陷量均显著增大,随机缺陷的筒壳左、右两侧凹陷区域形成了许多局部小的凸起和凹陷。

图3 四种缺陷筒壳在轴压和不均匀内压下弹性临界变形Fig.3 The critical deformation of shells under axial and non-uniform pressure with four kinds of imperfections
图4给出了四种缺陷筒壳在不均匀内压和轴压下最大内凹点的弹性径向位移与无量纲轴压的关系曲线,从该图中可看出,四种缺陷筒壳的最大内凹点的径向位移在达到临界应力后,均有按原曲线轨迹返回的趋势。可见,达到临界应力后,最大内凹区域已失去了继续承受均匀轴压荷载的能力,整个筒壳进入了屈曲后承载阶段。
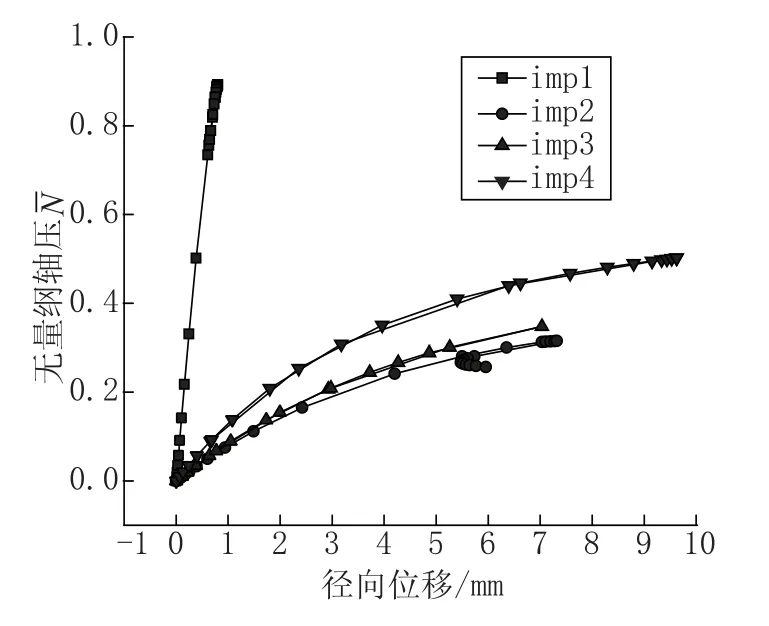
图4 四种缺陷筒壳在不均匀内压和轴压共同作用下最大内凹点的弹性径向位移与无量纲轴压的关系曲线Fig.4 The curve of maximum elastic radial displacement and relative axial force of shells under non-uniform pressure with four kinds of imperfections
2.六种偏心卸料工况的影响
其次考察了6 种偏心卸料工况对屈曲承载力的影响,表3给出了焊接缺陷形式A 模型在轴压和无量纲内压值为0.2 的6 种不均匀内压共同作用下的弹性无量纲临界应力。从表中可见,dp4 和dp5 两种偏心卸料状况下的临界应力最低。

表3 六种偏心卸料状况下的无量纲弹性临界应力Tab.3 The relative critical stress under six kinds of eccentric discharging cases
图5和图6给出了6 种卸料工况下不均匀内压施加完毕后的变形和在均匀轴压下达到临界应力时的变形。从不均匀内压施加完毕后各筒壳的变形可见,dp4 和dp5 两种卸料工况的不均匀内压在筒壳上所产生的局部凸起和凹陷量最大,特别是靠近卸料口侧仓壁的局部凹陷量最大,该处在后期均匀轴压的作用下最先进入屈曲状态。从达到临界应力时各筒壳的变形可见,在均匀轴压作用下,筒壳前期的局部凸起和凹陷量进一步增大,对于 dp6 卸料工况,其与卸料口中轴线成90°夹角处仓壁的内凹变形量最大,而其他5 种卸料工况均是与卸料口最近一侧仓壁的内凹变形量最大,这些区域在后续加载过程中失去了抵抗变形的能力,整个筒壳由于这些区域的局部屈曲而进入后屈曲承载阶段。
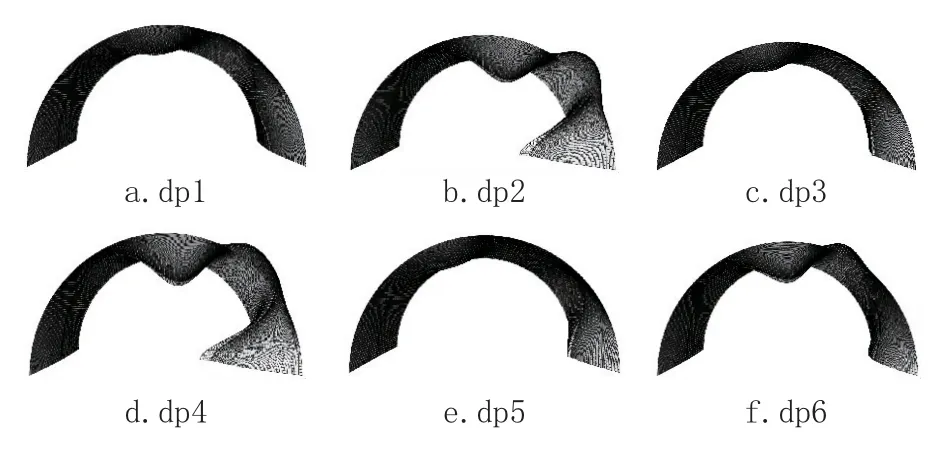
图5 六种卸料工况下不均匀内压施加完毕后变形Fig.5 The deformation of shells by non-uniform pressure under six discharging cases
图7给出了筒壳在6 种不均匀内压和轴压共同作用下最大内凹点的弹性径向位移与无量纲轴压的关系曲线,径向位移所取自的是与卸料口中轴线成90°夹角的内凹区域的最大内凹点,从该图中可看出,dp3 卸料工况下的径向位移最大,达到了40mm,其他几种工况该点的径向位移均较小。

图6 六种卸料工况轴压和不均匀内压下弹性临界应力变形Fig.6 The critical deformation by axial and non-uniform pressure under six discharging cases

图7 六种卸料工况下在不均匀内压和轴压共同作用下最大内凹点的弹性径向位移与无量纲轴压的关系曲线Fig.7 The curve of maximum elastic radial deformation and relative axial force by axial and non-uniform pressure under six discharging cases
2.2 弹塑性屈曲承载力分析
随后进行了dp5 偏心卸料工况下四种缺陷钢筒壳的弹塑性临界应力分析,不均匀内压的无量纲内压值=0.2,得到的无量纲临界应力如表4所示。从表中可见,一阶特征值屈曲模态缺陷的弹性临界应力和弹塑性临界应力相差不大,说明该钢筒壳屈曲时,局部凹陷区域尚未进入塑性状态,其他三种缺陷形式的弹塑性临界应力均低于弹性临界应力,说明钢筒壳在不均匀内压和轴压共同作用下,考虑材料弹塑性会削弱钢筒壳的临界应力。

表4 四种缺陷筒壳的无量纲弹塑性临界应力Tab.4 The relative critical elastic-plastic stress of four kinds of imperfections
最后进行了dp5 卸料工况下三种无量纲内压大小对焊接缺陷A 钢筒壳的弹性和弹塑性临界应力影响分析,三种不均匀内压的无量纲内压值=0.2、0.5、1.0,得到的无量纲临界应力如表5所示。从表中可见,无量纲内压值为 0.2 和0.5 时的弹性和弹塑性临界应力相差不大,当无量纲内压值为1.0 时,弹性和弹塑性临界应力均有较大的降低,特别是弹塑性临界应力只有经典屈曲应力的1%,可见,不均匀内压的增大对钢筒壳的临界屈曲应力有很大的削弱。
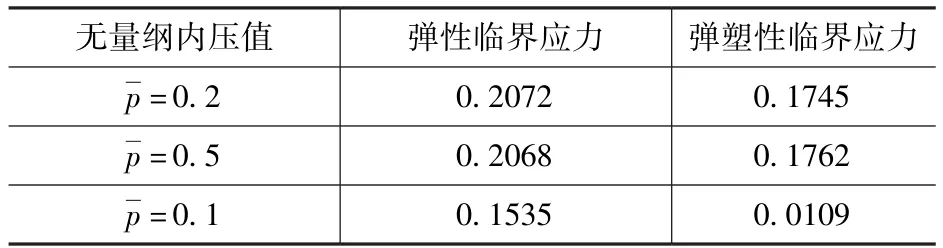
表5 三种无量纲内压筒壳的无量纲临界应力Tab.5 The relative critical stress under three kinds of relative inner-pressure
图8和图9给出了三种无量纲内压下钢筒壳最大内凹点的弹性和弹塑性径向位移与无量纲轴压曲线。从图中可看出,随无量纲内压值的增大,弹性和弹塑性临界应力降低,相同轴压下的弹性和弹塑性径向位移均增大。
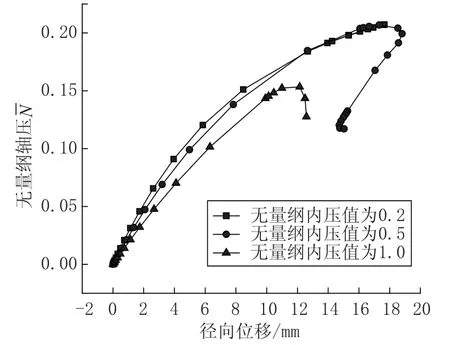
图8 三种无量纲内压筒壳最大内凹点的弹性径向位移与无量纲轴压曲线Fig.8 The curve of maximum elastic radial displacement and relative axial force of shells under three kinds of non-uniform pressure
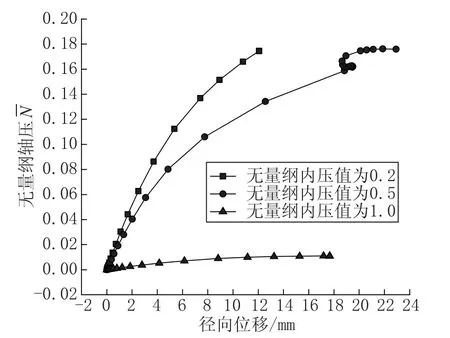
图9 三种无量纲内压筒壳最大内凹点的弹塑性径向位移与无量纲轴压曲线Fig.9 The curve of maximum elastic-plastic radial displacement and relative axial force of shells under three kinds of non-uniform pressure
3 计算公式的拟合
在前述分析的基础上,定义相同无量纲内压值的不均匀内压和轴压下的弹性临界应力与均匀内压和轴压下的弹性临界应力的比值为不均匀内压弹性折减系数ψecc,e,同理可定义不均匀内压弹塑性折减系数ψecc,p,这两个系数表示不均匀内压对钢筒壳临界屈曲应力的折减。
进行了包含表1列出的所有参数的有限元模型分析,得到了一系列的弹性和弹塑性屈曲极限承载力计算结果,在此基础上得到不均匀内压弹性和弹塑性折减系数,结果表明,弹性折减系数和弹塑性折减系数的下限值拟合出的曲线相差不大,故采用弹性和弹塑性折减系数共同的下限值拟合出不均匀内压折减系数ψecc与无量纲内压值的关系曲线如图10所示,可见该曲线与钢筒壳的高径比H/D以及径厚比R/t两个参数有关,由于篇幅所限,仅给出了R/t=500 的拟合结果,根据拟合曲线得到的不均匀内压折减系数ψecc计算公式如式(4)所示。

其中:系数A1=0.812,y1=-0.251,t1=0.147,b1=1.258,b2=-0.787,c1=-0.022,c2=0.026。
最后,可得到仓壁的弹性和弹塑性屈曲承载力的折减系数αecc,e和αecc,p,如式(5) 和式(6)所示。

为了对该拟合公式的可靠性进行验证,在ABAQUS 中建立了若干个钢筒仓的有限元模型,定义不同的偏心卸料工况,并计算得到了仓壁的不均匀内压折减系数,而后与拟合公式计算的结果进行了对比,如表6所示。

图10 不均匀内压折减系数和其下限值的拟合曲线Fig.10 The fit curve of non-uniform pressure reduction factor and low limit value
由表6可见,公式拟合结果均小于有限元结果且具有一定的安全余量,可见拟合公式具有一定的可靠性。
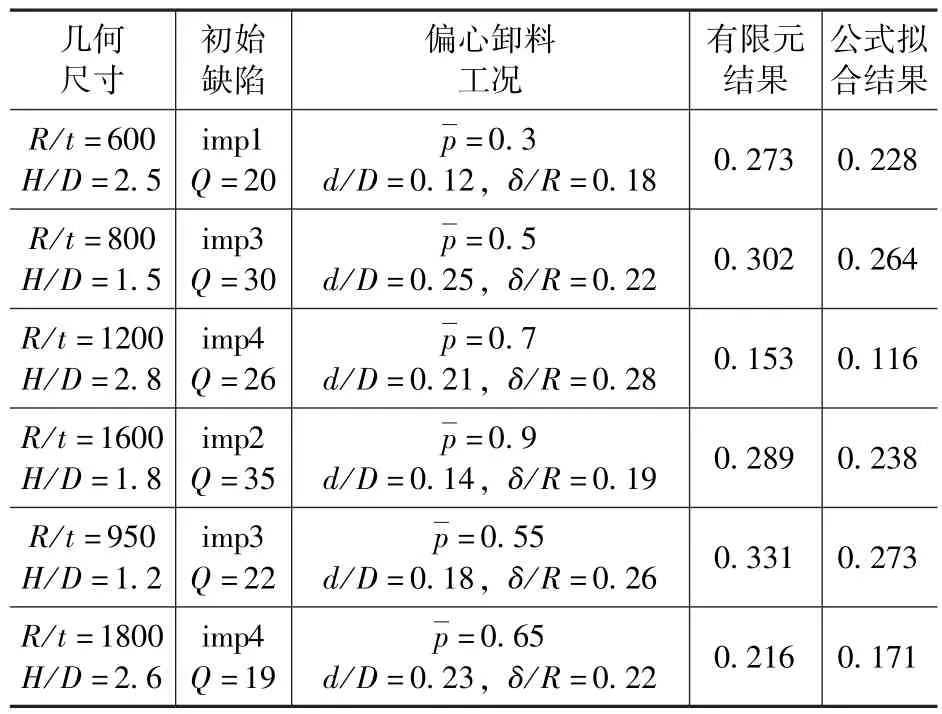
表6 拟合公式与有限元结果对比Tab.6 The comparison of fit formula and finite element
4 结论
本文对钢筒壳在轴压和不均匀内压下的屈曲承载力进行了有限元分析,得到了如下结论:
1.不均匀内压与相同量级的均匀内压相比,会显著降低钢筒仓仓壁的极限屈曲承载力,且随无量纲内压值的增大,轴压和不均匀内压共同作用下钢筒仓仓壁的极限屈曲承载力会随之降低;
2.不均匀内压的分布形式与不同缺陷形式的结合,会导致钢筒仓仓壁出现最小的极限屈曲承载力;
3.在有限元参数化分析基础上拟合出了轴压和不均匀内压下仓壁极限屈曲承载力折减系数的公式,对中国规范中筒仓临界屈曲应力的规定进行补充和完善。
