两种气动推力矢量技术的数值模拟研究

张建东， 王占学， 刘增文， 蔡元虎

（西北工业大学 动力与能源学院，陕西 西安710072）

0 引 言

由于机械式推力矢量喷管固有的缺点，如发动机重量的增加、高温环境下运动件的增多、冷却要求提高、隐身能力差、可靠性下降、成本增大等，使得很多的研究人员开始探索不需要机械调节的流体推力矢量喷管，即通过在喷管壁面的二次流的注入，从而实现主流方向的改变。这种基于二次流控制的推力矢量喷管与机械式推力矢量喷管相比具有明显的技术优势，从而成为喷管矢量控制研究的热点［1－5］。

综合起来，主要集中在三种控制方法，即激波矢量控制（Shock Vectoring controlling，SVC）［3－4］技术、喷管喉部偏移（Throat Shift，TS）［1－2］技术、反流控制（Counter Flow，CF）［6］技术。

本文采用数值模拟的方法，对激波矢量控制和喉部偏移两种喷管气动矢量控制方法的适用范围和相关特性进行了研究。

1 喷管几何结构与气动条件

1.1 几何结构

喷管几何外形［5，7－8］如图1所示。进口面积（高度）Ain＝0.09876，喉部面积（高度）Ath＝0.05283，膨胀比Ae／Ath＝1.1、1.2、1.3、1.4、1.5、1.6、1.7，以完全膨胀为原则所得各膨胀比所对应的设计落压比分别是3.059、3.858、4.640、5.432、6.243、7.076、7.933，喷管扩张段长度R＝0.0504，二次流喷射位置x／x1＝0.7247（取喷管喉部为轴向坐标0点，x1为喷管扩张段尾缘轴向位置），二次流喷射孔与喷管主流方向垂直，二次流喷射孔宽度为喷管喉部宽度的7.7%，二次流进口面积大于喷射孔喉部面积，在本文所研究的二次流压比条件下，二次流喷射孔出口达到声速。喷管外型面保持不变，而外型面尾缘随扩张段末端的移动而改变。

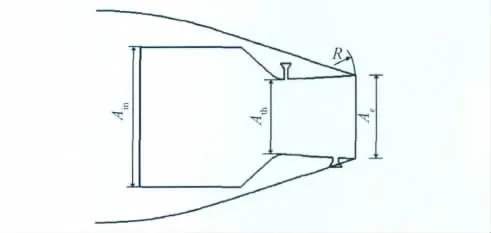
图1 喷管几何型面Fig.1 Nozzle geometry

1.2 气动条件

本研究中，假设喷管工作于海平面H＝0km，飞行马赫数Ma0＝0.3，气流方向角为0.0°，喷管进口气流总温321.6K。

2 喷管流场数值模拟计算方法

2.1 网格划分

为了准确模拟喷管流场，特将整个计算域划分为11个区域，其中喷管内部流场分为2个区域，两个二次喷射流共2个区域，自由流分为6个区域，喷管后部射流分为1个区域。对于远场边界，以喷管出口截面为参照，来流取5倍喷管出口长度，下游取6倍喷管出口长度，上下边界取7倍喷管外壁最大截面长度。需要说明的是，扩张段喷射孔入口的部分区域与外界小部分区域看起来重合，但实际相互之间并无干扰，网格划分见图2。

图2 计算网格Fig.2 Computational grids distribution

2.2 数值计算方法

整个区域共划分网格点16万，壁面y＋值接近1，并使用壁面插值函数。流场计算采用隐式格式求解对流项，采用有限体积法求解N－S方程，湍流模型选用k－ε模型。进口给定总压、总温和气流方向角，出口给定静压。相关气动参数均根据第1节中的设计参数给出。整个流场采用喷管进口参数进行初始化。

在本研究中，通过分别位于喷管上下两侧的喷射孔同时喷射实现TS法控制气动推力矢量；通过位于扩张段的喷射孔单独喷射而位于喉部上方的喷射孔关闭实现SVC法控制流体推力矢量。

3 流场计算结果与分析

3.1 典型流场结构分析

以落压比NPR＝4.0，二次流喷射孔进口总压与主流总压之比（称之为二次流压比）SPR＝1.0，膨胀比Ae／Ath＝1.4为例对两种流体推力矢量方式的流场进行对比，当位于喉部和扩张段的喷射孔都喷射气流时的流场计算结果见图3，只有扩张段喷射孔喷射时的流场计算结果见图4。

由图3可见，当喷管上下两侧喷射时，喷管气动喉部严重偏离喷管的几何喉部，喷管出口气流方向也随之发生了偏转。上侧喷射孔前分离区域位于喷管收缩段，从而对主流产生了阻塞作用，造成主流流量的减小。位于喷管喉部的喷射孔，其前后分离区域均小于扩张段喷射孔，原因是喉部的气流静压大于扩张段，使喉部二次流入射深度较小。

由图4可见，当扩张段喷射孔单独喷射时，二次流喷射对喷管声速线无影响（在本算例中，喉部下壁面处声速线略受扰动）。当主流压力不变时，二次流总压影响二次流的入射深度，从而影响喷射孔上游分离区域的大小。喷射孔下游分离区域内呈亚声速流动状态，所以该区域壁面压力与外界大气压相同［5］。

3.2 SVC法与TS法控制喷管矢量性能对比

为了确定TS法与SVC法控制喷管矢量性能对不同膨胀比喷管的适应范围，本研究对NPR分别为4和7时，喷管喉部高度相同，而膨胀比不同的喷管进行了流场特性的数值模拟，NPR＝4时喷管性能见图5，NPR＝7时喷管性能见图6。

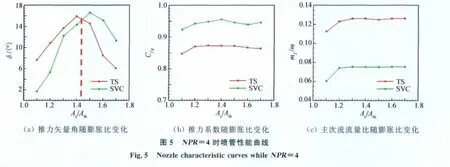
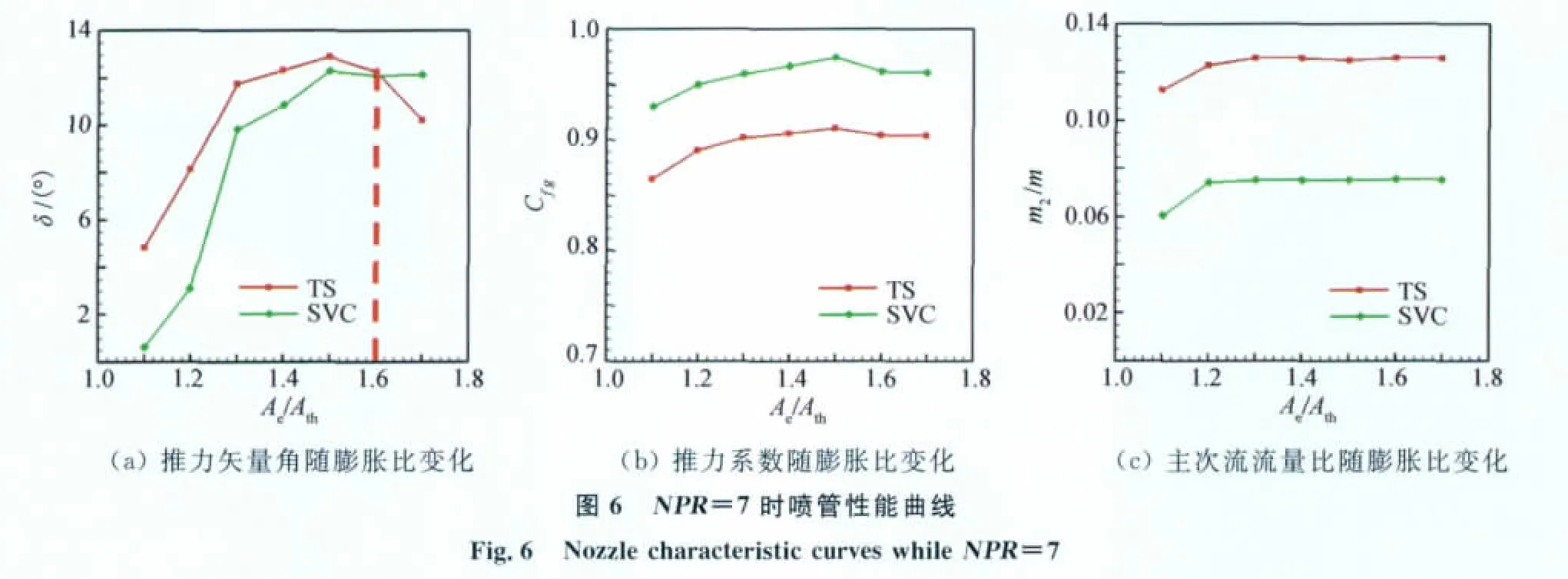
由图5（a）和图6（a）可见，喷管的膨胀比在约为1.5时是一个关键的分界点，当膨胀比小于1.5时，采用TS法使喷管的推力矢量角更大；而当膨胀比大于1.5时，采用SVC法使喷管的推力矢量角更大。由图5（b）和图6（b）可见，SVC法所对应的推力系数更大，这是因为采用TS法时，喉部上方的喷射时主流流量减小，从而使TS法所对应的推力系数小于SVC法，同时，不同膨胀比所对应的推力系数有一个峰值。由图5（c）和图6（c）可见，SVC法主、次流流量比小于TS法，这是因为TS法有上、下两个喷射孔同时在注入二次流气体，同时二次流流量几乎不随膨胀比变化，由此可见，决定主、次流流量比的主要因素是二次流与主流总压比（SPR）。

4 结 论

根据对具有不同膨胀比二元收扩喷管的流场数值模拟计算，可以得出如下结论：

（1）TS法与SVC法所对应的喷管声速线具有不同的分布特征，TS法使喷管声速线发生严重扭曲，而SVC法对喷管声速线无影响；

（2）不同膨胀比所对应的最优矢量控制方法不同，当膨胀比小于1.5时，宜采用TS法控制喷管推力矢量角，而膨胀比大于1.5时，则须采用SVC法；

（3）TS法在控制喷管气动矢量角度的同时，还可以限制喷管主流流量。

［1］MILLER D N，YAGLE P J，HAMSTRA.Fluidic throat skewing for thrust vectoring in fixed geometry nozzles［R］.AIAA 99－0365.

［2］YAGLE P J，MILLER D N，GINN K B，et al.Demonstration of fluidic throat skewing for thrust vectoring in structurally fixed nozzles［J］.JournalofEngineering forGasTurbinesandPower，2001，123：502－507.

［3］JIMENEZ A，MADRID.Thrust vectoring for advance fighter aircraft，propulsion package development［R］.AIAA 2001－3991.

［4］MANGIN B，CHPOUN A，JACQUIN L.Experimental and numerical study of fluidic thrust vectoring of a two－dimensional supersonic nozzles［R］.AIAA 2006－3666.

［5］王占学，李志杰.喷管气动参数对推力矢量影响的数值模拟［J］.推进技术，2008，2.

［6］SANTOS M M.Experimental study on counter flow thrust vectoring of a gas turbine engine［D］.［Doctor′s Degree Dissertation］.The Florida State University College of Engineering，2005.

［7］李志杰，王占学.二次流喷射位置对流体推力矢量喷管气动性能影响的数值模拟研究［J］.航空动力学报，2008，9.

［8］李志杰，王占学.基于激波控制的流体推力矢量喷管数值模拟及试验模拟［R］.天津：2008年中国工程热物理学会年会，2008.