活跃在中考中的动态问题分类探究

2012-11-07

中学教研(数学) 2012年5期

关键词：考试题四边形抛物线

●

(钱岗中学湖北枣阳 441221)

活跃在中考中的动态问题分类探究

●莘义成

(钱岗中学湖北枣阳 441221)

动态问题是近年来中考中的一个热点题型，一般是以压轴题的方式出现.它综合了代数(函数与方程)、空间图形、三角形等知识，通过几何元素(点、线、三角形、四边形、圆)的运动变换，结合其他数学知识形成.这类题综合性强、开放度高，解答的关键是要理解图形运动前后各元素之间的数量关系，善于抓住其中不变的量和变化规律，能从运动变化的角度去思考问题，从而找到解题的突破口，还要综合运用数形结合、分类讨论、方程、函数、转化等数学思想方法去探索解题的思路.它考查面广，涉及的知识点众多，留给学生很大的思维空间和思维量，需要我们在运动中分析，在变化中求解.本文以2011年全国各地中考出现的动点类问题为例进行分析，以供参考.

类型1动态问题与函数图像结合

图1

例1如图1，正方形ABCD的边长为4，P为正方形边上一动点，运动路线是A→D→C→B→A，设点P经过的路线为x，以点A，P，D为顶点的三角形的面积是y．则下列图像能大致反映y与x的函数关系的是

( )

A. B. C. D.

(2011年四川省宜宾市数学中考试题)

分析当点P在AD上运动时，0≤x≤4，△APD不存在，面积为0；当点P在DC上运动时，4≤x≤8，△APD随着点P的运动面积逐渐增大，当点P到达点C时，△APD面积为8；当点P在BC上运动时，8≤x≤12，△APD随着点P的运动面积不变仍为8；当点P在AB上运动时，12≤x≤16，△APD随着点P的运动面积逐渐减小，当点P到达点A时，面积为0.故选B．

点评本题是一道以点运动为背景的图像信息题，解答时必须分情况讨论，从图形和图像上捕获信息.本题涉及分段函数问题、几何问题，考查观察、分析、建模、判断等能力，具有一定的综合性．

类型2三角形中的动态问题

例2如图2，在平面直角坐标系xOy中，直线AB与x轴交于点A，与y轴交于点B，且OA=3，AB=5．点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AO返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P,Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB-BO-OP于点E．点P,Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P,Q运动的时间是t(t>0)秒．

(1)求直线AB的解析式.

(2)在点P从O向A运动的过程中，求△APQ的面积S与t之间的函数关系式(不必写出t的取值范围).

(3)在点E从B向O运动的过程中，完成下面问题：

①四边形QBED能否成为直角梯形？若能，请求出t的值；若不能，请说明理由.

②当DE经过点O时，请直接写出t的值．

(2011年福建省泉州市数学中考试题)

分析(1)在△AOB中,由勾股定理可求出点B的坐标，从而求出直线AB的解析式.

(3)当DE∥QB或PQ∥BO时，四边形QBED都是直角梯形，用相似三角形的判定和性质，构建出一元一次方程解答即可.

(3)当DE∥QB或PQ∥BO时，四边形QBED能成为直角梯形．

①如图4，当DE∥QB时，因为DE⊥PQ，所以PQ⊥QB，从而四边形QBED是直角梯形，∠AQP=90°．由△APQ∽△ABO得

故

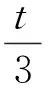
解得

点评本题的动点在三角形的3条边上运动，在第(1)小题中由线段的长转化为点的坐标，进而可求出直线的解析式；第(2)小题用变量表示出三角形的面积，关键是用变量表示三角形的底和高；第(3)小题需在运动中的特殊时刻组成特殊的四边形，根据点的运动情况，合理构建出对应的图形是解答本问的关键.本题把函数、方程、勾股定理、直角梯形、相似三角形的判定和性质等众多知识整合在一起，渗透了数形结合、分类讨论、方程等的思想方法，具有较强的综合性.本题可变式为“当t为何值时，△APQ是等腰三角形”.

类型3四边形中的动态问题

(1)求点B，C的坐标；

(2)求S随t变化的函数关系式；

(3)当t为何值时，S有最大值？求出最大值.

(2011年山东省烟台市数学中考试题)

图6 图7

图8 图9

(2)根据点P的运动情况，应分为3种情况：当点P在AO上时，0

(3)根据第(2)小题的3种情况，分别计算出S的最大值，然后进行比较.

(2)作CM⊥AB于点M，QN⊥AB于点N，则CM=4，BM=3,从而

①如图7，当0

③如图9，当5

2t-8(5

点评本题中随着点的运动，△OPQ也随之发生变化，因此要对运动中的各类情况进行分类讨论，明确点P运动过程中的关键点(分界点)，从而构造出不同的图形，用变量表示出△OPQ的底和高是解答的关键.本题考查一次函数的图像和性质、勾股定理、锐角三角函数、二次函数、梯形的性质等知识点，具有较强的探索性和综合性.

类型4圆中的动态问题

图10

例4如图10，在平面直角坐标系中，点A(10，0)，以OA为直径在第一象限内作半圆C，点B是该半圆周上的一动点，联结OB，AB，并延长AB至点D，使DB=AB，过点D作x轴的垂线，分别交x轴、直线OB于点E，F，点E为垂足，联结CF.

(1)当∠AOB=30°时，求弧AB的长.

(2)当DE=8时，求线段EF的长.

(3)在点B运动过程中，是否存在以点E，C，F为顶点的三角形与△AOB相似？若存在，请求出此时点E的坐标；若不存在，请说明理由.

(2011年浙江省金华市数学中考试题)

分析(1)易知∠ACB=60°,根据弧长公式即可求出.

(2)联结OD，在△ODE中，由勾股定理可求出OE的长，然后利用三角形相似可求得EF的长.

(3)在点B的运动中，点E，F的位置也随之发生变化，应分交点E在O，C之间、在点C的左侧和在点C的右侧3种情况，分别画出图形，利用相似构建出方程予以解答.

(2)如图11，联结OD.因为OA是⊙C直径,所以∠OBA=90°.又因为AB=BD,所以OB是AD的垂直平分线,即OD=OA=10.

在Rt△ODE中，由勾股定理可得OE=6,从而AE=4.易证△OEF∽△DEA,可得EF=3.

图11 图12

图13 图14

(3)设OE=x.

①如图12，当交点E在O，C之间时，由以点E，C，F为顶点的三角形与△AOB相似，有∠ECF=∠BOA或∠ECF=∠OAB.

点评本题是以动点和三角形相似结合的综合性压轴题，具有较强的综合性.考查学生观察、分析、构建图形的能力，把动态问题变为静态问题，从点的不同位置入手，将每种运动变化情况单独用图形进行表示的能力.本题涉及圆的有关性质、相似三角形、一元二次方程等知识，要注意把各种情况考虑全面，构建出每种情况的图形是解题的关键.

类型5抛物线中的动态问题

例5如图15，在平面直角坐标系xOy中，△ABC的2个顶点A，B在x轴上，顶点C在y轴的负半轴上．已知|OA|∶|OB|=1∶5，|OB|=|OC|，△ABC的面积S△ABC=15，抛物线y=ax2+bx+c(a≠0)经过点A，B，C．

图15 图16

(1)求此抛物线的函数表达式.

(2)如图16，设E是y轴右侧抛物线上异于点B的一个动点，过点E作x轴的平行线交抛物线于另一点F，过点F作FG垂直于x轴于点G，再过点E作EH垂直于x轴于点H，得到矩形EFGH．则在点E的运动过程中，当矩形EFGH为正方形时，求出该正方形的边长.

(2011年四川省成都市数学中考试题)

(2)设点E的坐标为(m,m2-4m-5)，抛物线的对称轴为x=2，根据2(m-2)=EF，列方程求解.

解得

m=1,m=-1(舍去负值).

从而

A(-1，0)，B(5，0)，C(0，-5)，

得抛物线的解析式为

y=x2-4x-5．

(2)设点E的坐标为(m,m2-4m-5)，抛物线的对称轴为x=2，由EF=2(m-2)，得

2(m-2)=-(m2-4m-5)

或

2(m-2)=m2-4m-5，

解得

点评本题考查了二次函数的综合运用．根据点的运动带来图形的变化，由正方形的性质构成一元二次方程组求解.第(3)小题探讨存在性问题，此类问题是先假设存在，然后进行推理，分2种情况进行解答，根据函数与方程的转化与应用，可组成2个不同的方程组，解出即得问题的解.本题的关键是采用形数结合的方法，准确地用点的坐标表示线段的长，根据图形的特点，列方程求解，注意分类讨论．

类型6几何图形变换中的动态问题