质疑深究 收获精彩

●

(天台中学高二(2)班 浙江天台 317200)

质疑深究收获精彩

●褚壹钦

(天台中学高二(2)班 浙江天台 317200)

有时候，对教师的讲授是不能过分的相信，因为教师也有出错的时候，对教师的讲授要质疑深究,这样才能获益非浅，也许还能收获精彩.下面就是一个很好的例子.

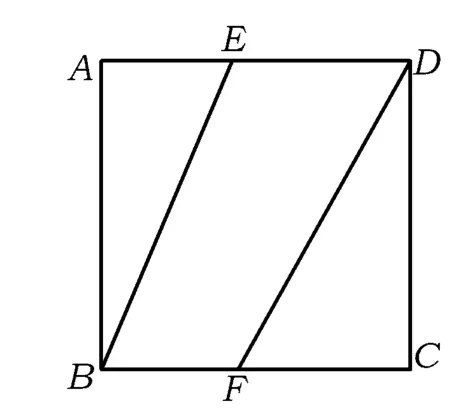
图1

例1如图1，在正方形ABCD中，E，F分别为线段AD，BC上的点，∠ABE=20°，∠CDF=30°．将△ABE绕直线BE，△CDF绕直线CD各自独立旋转一周，则在所有旋转过程中，直线AB与直线DF所成角的最大值为________．

(2011年浙江省数学高考样卷试题)

老师是这样讲授的．按照题意的要求，得到如图2所示的2个圆锥，即圆锥B-AA1和圆锥D-FF1；这样，2个圆锥上各任意取一条母线，这2条母线(大多是异面直线关系)所成的角是因为空间关系太远就很难想象或求出来．要求学生根据异面直线所成角的定义及常用求法思考如何改变圆锥的位置，创造条件来求．

1 质疑

图2 图3

这样，老师就启发学生把圆锥D-FF1平移，如图3．过了一会儿，空间想象力强的几个学生就已经发现所要求的答案是70°，经他提醒，大部分学生都已经明白这个结果,即当2条母线分别是BA1，BN时，所求的夹角为最大．

在本题即将要结束时，老师顺便问了“那么，你们看直线AB与直线DF在什么时候，所成角又是最小呢？是多少呢？学生课后去思考一下；这个答案是10°，答案先给你们，以便检验自己的思考．”

真的是10°吗？课后许多学生陷入思考之中．

2 深究

课后，包括笔者在内的4位学生组成学习小组，准备对这一试题做全面地研究和探索．

其实，探究直线AB与直线DF所成的角，在图3中思考还是很困难的！有学生提出，既然在图3中∠A1BN=110°，所求目标的最大值70°就是在这个位置上，因此我们可以考虑圆锥B-MN的反向部分与圆锥B-AA1的关系，这样就得到图4．

由图4可以发现，要求的异面直线夹角的最大值确实是BM1与BA1所成的角即70°.此时，圆锥B-AA1与圆锥B-M1N1之间有公共部分，有学生怀疑这公共部分可能不是直线，如果是那就是公共母线了，所求异面直线所成的角最小值就不是10°了，应该是0°了．

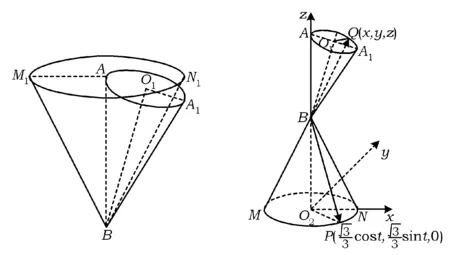
图4 图5

2 收获精彩

为了弄清楚这个问题，笔者所在的学习小组着手研究，同时也把这样的想法报告了老师，引起了老师的注意．

在老师的指导下，我们想到了建立空间直角坐标系，用向量工具解决上面的问题．方法如下．

而点Q要满足什么条件呢？经过学生思考、讨论、挖掘，发现点Q就在2个曲面的公共点上，即球面和平面的公共点上；球面就是以B为圆心、1为半径的球面，满足的方程是x2+y2+(z-1)2=1；平面是过点A、垂直于xO2z的平面，在x轴上的截距为2tan70°，从而平面方程为

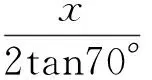
这样点Q就可以由方程组

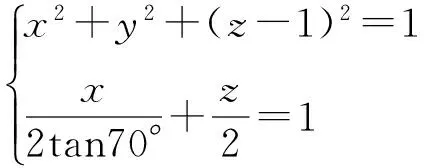
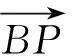
由异面直线夹角定义可得

即

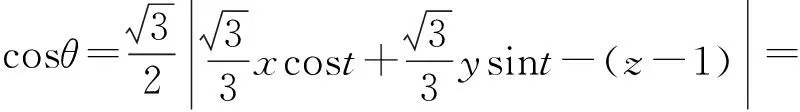
由图像直观可知，这个z-1>0，经过计算可知2≥z≥1+cos40°,令z-1=cosα，α的范围是0°≤α≤40°.

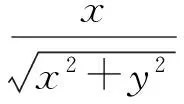
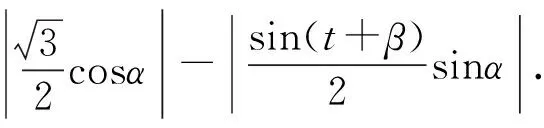
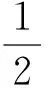
cosθ=sin(α+60°)，

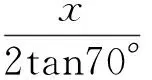
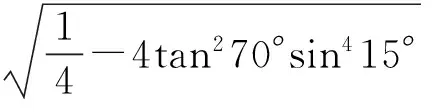
再求β的值，后由sin(t+β)=-1可以求得t的值，即证明了“取到最小值”的存在性．这就充分肯定了上面的怀疑，即这里的2个圆锥面的公共部分应该是直线(公共母线)．

综上所述,直线AB与直线DF所成角的范围为0°～70°．

通过对该试题的钻研，笔者得到了几点启发：

(1)数学试题数量浩如烟海，是无尽的；对数学例、习题的钻研，先要保证质量，后方可上数量．

(2)学习要有质疑的精神，质疑是获得问题的来源，而深入探究又是获得数学知识与解题经验的契机．

(指导老师：王修凯)