用好课程资源 激发学生探究——高中数学探究性教学的实践与反思

●

(元济高级中学 浙江海盐 314300)

用好课程资源激发学生探究
——高中数学探究性教学的实践与反思

●刘凤杰卢明

(元济高级中学 浙江海盐 314300)

数学的探究活动能促进学生将新旧知识进行有效地重组，获得深切的感受与体验，让学生有一个自主建构知识的过程，学会学习，养成良好的学习、质疑和反思的习惯，增强创新能力．因此，数学探究是贯穿于整个高中数学课程始终的重要内容．笔者通过教科书上的一道解析几何探究题(人教A版《数学》2-1第55页)开展探究性教学，说明“用好课程资源，实施探究性教学”是值得广大高中数学教师关注的新途径．

1 案例

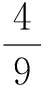
与课本中例2.2和例3比较，你有什么发现？

1．1 初步探究，解决问题

学生经过自主探究，很快得出了点P的轨迹方程，并发现“平面上，如果一个动点到2个定点连线的斜率之积为一个正的常数，那么这个动点的轨迹为双曲线”这个更一般化的结论．

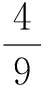
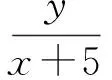
化简得

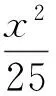
师：谁能从本题中提炼出一般化的结论？

生：设A(-a,0)，B(a,0)(a>0),直线PA,PB相交于点P，且它们的斜率之积kPA·kPA=λ(λ为常数，λ>0)，则点P的轨迹是以A,B为顶点的双曲线(不包括点A,B)．

1．2 比较探究，激发兴趣

师：请比较例2．2和例3，在刚才得出的命题中，如果撤消对λ的取值限制，你又可以得出什么样的结论呢？

学生思考以后，得到命题1,教师充分肯定了学生的发现.

命题1设点A(-a,0),B(a,0)(a>0)，直线PA,PB相交于点P，且它们的斜率之积是λ(λ≠0)，则

(1)当λ=-1时，点P的轨迹是圆

x2+y2=a2(x≠±a)；

(2)当λ<0(λ≠-1)时，点P的轨迹是椭圆

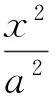
(3)当λ>0时，点P的轨迹是双曲线

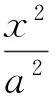
1．3 逆向探究，完善思维

师：如果已知点A,B是相应椭圆的长轴或双曲线实轴的端点，那么又会有什么新的发现呢？

沉默片刻，许多学生发现了命题2,教师再次肯定了学生的发现．

命题2(1)圆x2+y2=a2上任意一点P与A(-a,0),B(a,0)连线的斜率之积kPA·kPB=-1(定值)；

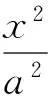
1．4 拓展探究，提升能力

师：在命题2的结论(1)中，在圆的背景下，对于圆上的3个点P，A，B，满足kPA·kPB=-1，你又有什么联想？

生1：我认为对于圆x2+y2=a2上任意一点P来说，不仅是它与点A(-a,0)和点B(a,0)连线的斜率满足kPA·kPB=-1，其实过圆心的任何一条直径的2个端点与点P连线的斜率之积都等于-1(直径所对的圆周角是直角)．

生2：我同意！我觉得还可以得出下列结论.

命题3(1)圆x2+y2=a2上任意一点P与该圆上关于坐标原点对称的2个点A(x0,y0),B(-x0,-y0)连线的斜率之积kPA·kPB=-1；

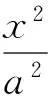
限于篇幅，这里只提供结论(2)的证明．

证明设P(x′,y′)为椭圆上异于A(x0,y0)和B(-x0,-y0)的任意一点，则

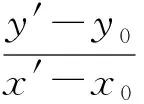
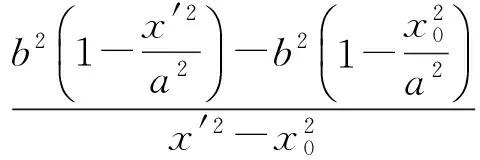
1．5 再逆探究，另辟蹊径

学生对上述命题及其证明都表示惊叹，探究的欲望更加强烈．在经过前面的探究经历后，学生的思维更加活跃，许多学生又得出如下命题：

命题4(1)设A，B是圆x2+y2=a2上2个不同的点，P是该圆上任意一点，且满足kPA·kPB=-1，则直线AB过定点O(0,0)；

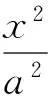
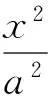
结论(2)和(3)的证明给学生带来了麻烦，于是，教师让学生合作尝试证明，最后有学生给出了证明.限于篇幅，这里仅提供结论(2)的证明.

证明设P(x0,y0)为椭圆上异于A和B的任意一点，A(x1,y1)，B(x2,y2)，直线AB方程y=kx+t，与椭圆方程联立，得

(b2+k2a2)x2+2kta2x+a2t2-a2b2=0，

从而

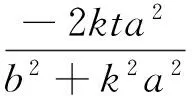
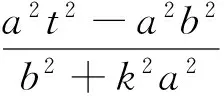
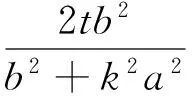
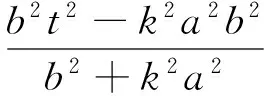
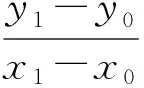
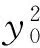
t2-(kx0+y0)t=0，

即

t(kx0-y0+t)=0.

因为P与A,B不重合，所以kx0-y0+t≠0，故t=0，即直线AB过定点O(0,0)．

1．6 发散探究，勇于创新

教师充分肯定了学生善于思考和探究的品质，鼓励学生作进一步的探究．此时，有学生发言.

生：我有一个问题：如果命题4中相应的定值发生改变，那么直线AB是否还过定点？

这一问，把教师也问住了，快下课时，教师坦然回答：刚才这个问题事先没考虑过，把这个问题作为今天的课后作业，希望在下次课上能够分享大家探究的成果．2天后，虽然大家没有得到更一般性结论，但有丰厚的回报．有学生得出以下命题：

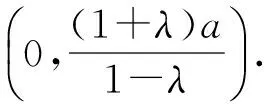
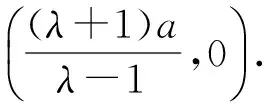
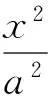
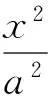
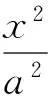
这里仅介绍学生给出的结论(4)的证明．

证明若A,B关于y轴对称，不妨设A(x0,y0)，B(-x0,y0)，则

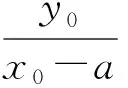
反之亦成立．

若A,B不关于y轴对称，设A(x1,y1)，B(x2,y2)，直线AB方程x=my+t与椭圆方程联立，得

(a2+m2b2)y2+2mtb2y+b2t2-a2b2=0,

从而

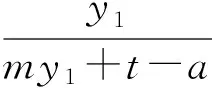
(λm2-1)y1y2+λm(t-a)(y1+y2)+λ(t-a)2=0.

将式(5)，式(6)代入，得

(λa2-b2)t2-2λa3t+a2b2+λa4=0,

即

[(λa2-b2)t-(λa3+ab2)](t-a)=0.

师：请大家回想一下以前做过的一道题目：

设A,B是抛物线y2=2px(p>0)上2个不同的点，O是该抛物线的顶点，且OA⊥OB，求证：直线AB过定点(2p,0)．

师：请对此题进行一般化的改造．

学生经过探究，得到以下命题：

证明设A(x1,y1),B(x2,y2)，直线AB的方程为

x=my+t,

与抛物线方程联立，得

y2-2pmy-2pt=0,

从而

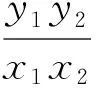
(λm2-1)y1y2+λmt(y1+y2)+λt2=0,

将式(7)，式(8)代入，得

2pt+λt2=0.

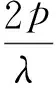
点评由教科书中的一道探究题，教师与学生一起做了这么一篇“大文章”，使人充分感受到了数学的创造美！在猜想与探究的过程中，学生的创新能力得到了培养，也让教师领会到学生的巨大智慧和能量．今日之教学，教师的责任首先是要激发学生的探究兴趣，点燃他们智慧的火花，释放他们探究的能量，让成功的喜悦伴随着创造的全过程．

2 体会与反思

2．1 钻研教材，合理利用课程资源

普通高中课程标准实验教科书人教A版《数学》，试图通过渗透以引导学生主动学习为核心的教学设计，达到引领教学方式变革之目的．即在每节教材中穿插“观察”、“思考”、“探究”之类的栏目，提出问题，引导学生主动学习．以高中数学解析几何内容为例，教材中一共安排了29个探究问题(包括探究与发现、信息技术应用)，其中必修2中有8个，选修2-1中有13个，选修4-4中有8个． 从大的类型分：一般探究问题有20个；探究与发现有4个；信息技术应用5个．这些探究问题既有针对具体内容的，也有针对思想方法的，还有针对特例、细节的，它们构成解析几何的学习主线，形成思想内涵丰富的解析几何的概念网络，体现新课标理念，着眼于学生知识的形成和知识发展规律，着眼于培养学生的创新精神和实践能力．

作为一名数学教师，应该领悟教材编者的意图，课本“探究栏目”提供了一个集探究和文化于一体的完美平台．由前面的案例可以看到，在日常教学中，合理地开发和利用课程资源，可以取得知识教学与能力培养两不误的效果．关于课本“探究栏目”这一课程资源的开发与利用，笔者有2点建议：(1)教师必须根据课本中探究题的类型，针对不同层次的学生，要有不同深度的探究设计；针对不同的教学内容，要有不同广度的探究设计．(2)在注意教法层次性的同时，还必须注意教法的多样性和开放性，给学生留下充分的活动时间与空间，培养学生的钻研精神和合作精神，让不同层次的学生都能学有所获．

2．2 鼓励提问，激发探究兴趣

首先，要了解数学探究性学习的内涵.即学生围绕某个数学问题，进行自主探究、学习，从中获得知识、技能和态度的学习方式和学习过程，包括：观察分析数学事实、提出有意义的数学问题、猜测探求适当的数学结论或规律、给出解释或证明．其次，要明确学生的探究学习起源于对某个问题的兴趣.空洞的说教并不能激起学生持久的探究欲望，正如爱因斯坦所指出的那样:“兴趣是最好的老师，它永远胜过责任感．”唯有兴趣，才是学生积极探究、主动学习的原动力．再次，要鼓励学生提问．学生提出一个有价值的问题比回答出10个教师预设的问题更有价值．现实中，主动向教师提问题的学生并不多，即便有，问的也大多是作业中自己不能解决的问题．因此，教师必须把“发现问题，提出问题”的意识和能力作为学生探究能力培养的重点．此外，教师要善于把握时机，创设问题情境，把问题抛给学生，引导学生去质疑、去发现，可以有效地培养学生发现问题、提出问题的能力，学生一旦能够提出问题，自然就有了探究的兴趣．

2．3 把握角色，谨防假探究

在探究性教学的过程中，教师的角色就是一名“催产婆”，而不是先知先觉的“圣人”．在实施探究性教学的过程中，如果教师为了让学生能够顺利地“猜出”教师需要的“答案”，将探究任务设计得面面俱到，过度引导学生朝某个方向探究，看起来学习过程自然流畅，其实是一种“假探究”．需要强调的是：探究需要给学生预留一定的思维空间和有一定难度的学习任务．当然，完全放任也是不对的，鼓励学生自主探究，不等于让学生脱离教师去单打独斗，要知道探究的形成是基于一定的问题引领下，学生通过独立尝试，在解决问题的过程中实现的．至于问题的由来，自然很大程度上离不开教师的引导、启发和指点．此外，在探究学习的过程中，教师能否为学生营造一个有利于促进学生探究活动深入进行的互动场，也是探究能否持续、获得成功的重要因素．

总之，在中学数学教学中，引导学生开展探究活动，是培养学生创新精神和实践能力的重要途径，它有利于培养学生对数学的情感，增强学生学习数学的自信和克服困难的意志力；有利于培养学生自主意识和合作精神，促进学生的全面发展．作为一名数学教师，必须预以重视，并自觉践行．