应用G′/G展开法求Davey-Stewartson I方程的精确解
2012-11-07冯庆江
冯庆江
(凯里学院 数学科学学院,贵州 凯里 556000)
1001-5051(2012)04-0375-06
应用G′/G展开法求Davey-Stewartson I方程的精确解
冯庆江
(凯里学院 数学科学学院,贵州 凯里 556000)
通过应用G′/G展开法,求出了复系数Davey-Stewartson I方程的精确解,并对解的性质进行了相应的分析研究.
G′/G展开法;复系数;Davey-Stewartson I方程;精确解
0 引 言
随着科学技术的不断发展,非线性科学在数学、物理学、力学、材料科学、通信技术、生命科学和计算机技术等领域的应用已经变得越来越广泛.最近几十年来,许多学者发现了一系列求解非线性偏微分方程的方法,如Bäcklund变换法[1]、Painlevé展开法[2]、齐次平衡法[3]、函数展开法[4]、混合指数法[5]、Hirota变换法[6]、分离变量法[7]、F-展开法[8]、辅助方程法[9]、形变映射法[10]等.最近,李帮庆等[11]利用G′/G展开法成功地求解了不同类型的非线性偏微分方程.本文以Davey-Stewartson I方程[12]
为模型,应用G′/G展开法求方程(1)的精确解,并对解的性质作简单的分析研究.式(1)中:u为复函数;v为实函数;r为实常数,i为虚数单位.
1 G′/G展开法的主要思想
首先,考虑非线性偏微分方程

式(2)中:u=u(x,y,…,t)是未知函数;F是关于u及u的各阶偏导数的多项式.应用G′/G展开法求解方程(2)的具体步骤如下:
步骤1 通过行波变换将变量x,y,…,t转化为行波变量ξ,假设

这样,式(2)就可以转化为只含有行波变量ξ的常微分方程
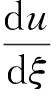
步骤2 将方程(4)的解表示成G′/G的多项式
式(5)中,G=G(ξ)满足
式(5)中的a0,a1,a2,…,am及式(6)中的λ,μ均为待定常数,且am≠0.正整数m的具体值可通过齐次平衡法来确定.
步骤3 将式(5)代入式(4),这时式(4)的左边变成一个关于G′/G的多项式,合并G′/G的相同幂次项,令该多项式的各阶G′/G幂次项的系数为零,导出关于以a0,a1,a2,…,am,α,β,…,η,λ,μ为未知量的非线性代数方程组.
步骤4 求解上述以a0,a1,a2,…,am,α,β,…,η,λ,μ为未知量的非线性代数方程组的解,通过式(6)可以求出G的值,从而进一步确定出G′/G,将a0,a1,a2,…,am,α,β,…,η,λ,μ和G′/G代入式(5),即可以求出方程(2)的行波解.
2 G′/G展开法的应用
下面应用G′/G展开法求解Davey-Stewartson I方程(1).由于u为复数,于是令

式(7)中:ξ=δx+ζy-ωt;η=αx+βy-γt;i2=-1.分别求出ut,uxx,uyy,vxx,vyy,(|u|2)xx,并将它们代入方程(1)的第1个方程,化简并分离实部和虚部,得


根据式(9)可以确定
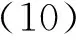
将ut,uxx,uyy,vxx,vyy,(|u|2)xx代入方程(1)的第2个方程,得

联立式(8)和式(11)得方程组
设φ和v具有如下形式:
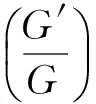

式(13)和式(14)中,G=G(ξ)满足式(6).通过式(6)可以得到
分别求出φ",v",φ3,φv,φ′2,φφ",并将它们代入方程组(12),这时方程组(12)的左边是一个关于G′/G的多项式,令该多项式的各阶G′/G幂次项的系数为零,得出以a0,a1,a2,…,am,α,β,…,η,λ,μ为未知量的非线性代数方程组
求解上述方程组,可得以下5组解:
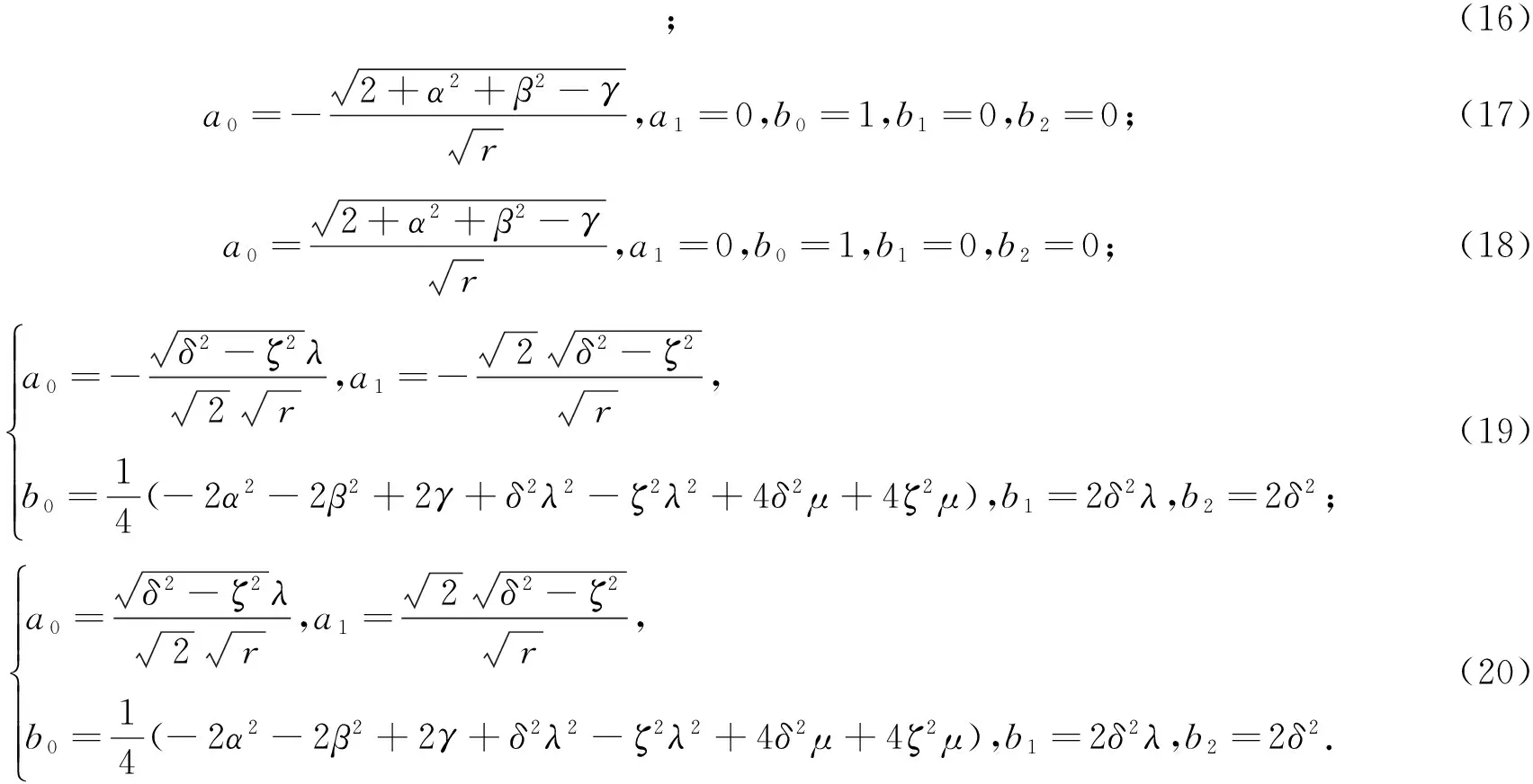
下面分3种情况进行讨论:
情形1当λ2-4μ>0时,
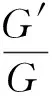
(22)
式(21)和式(22)中,ξ=δx+ζy-ωt(以下同).将式(13),式(14),式(16)~式(22)代入式(7),可以得到以下Davey-Stewartson I方程的5组解:
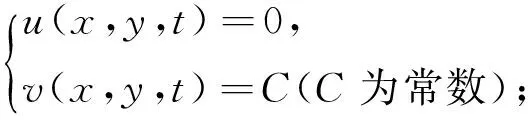
(23)

(24)
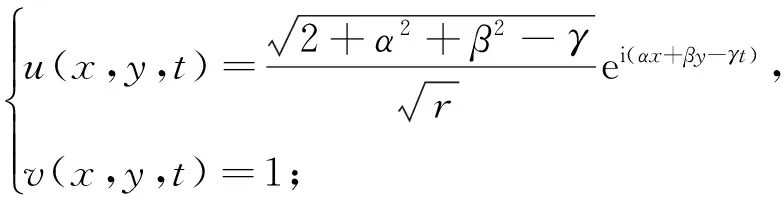
(25)
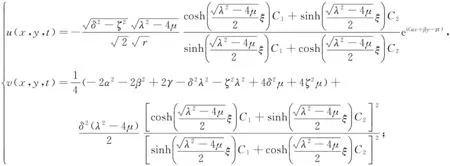
(26)
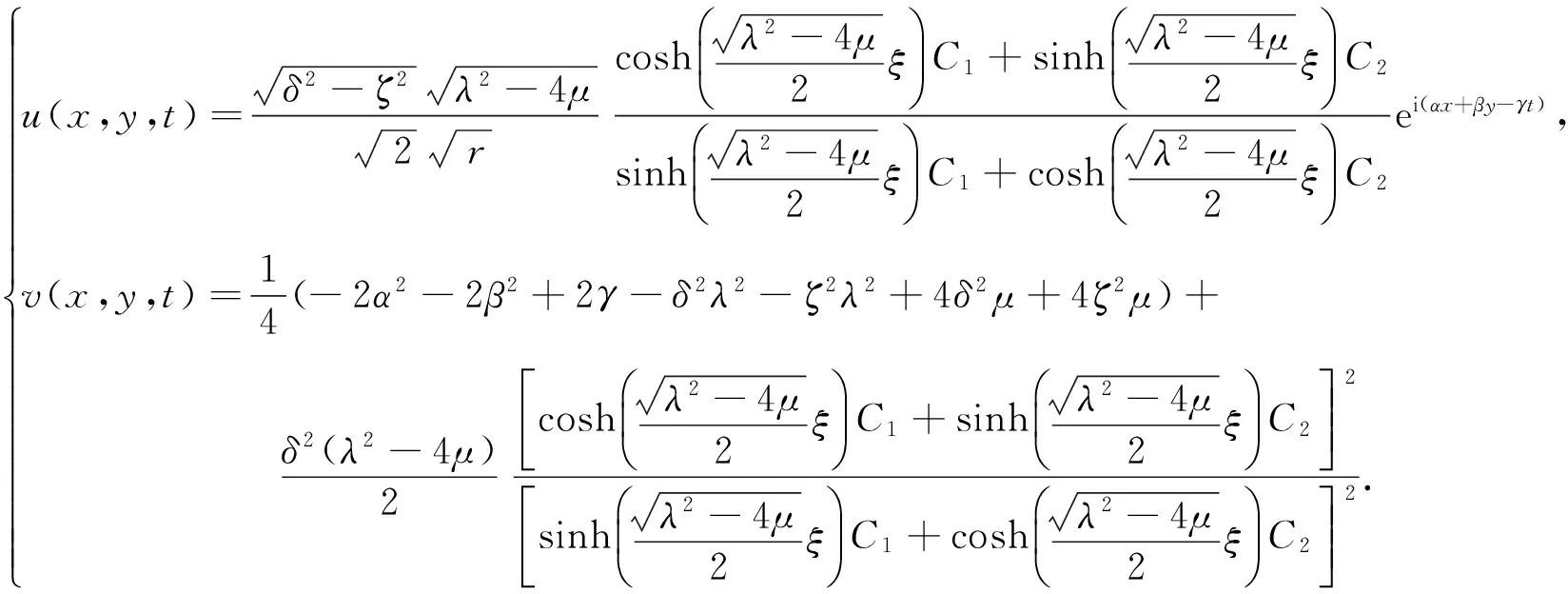
(27)
情形2当λ2-4μ=0时,
将式(13),式(14),式(19),式(20),式(28)和式(29)代入式(7),可得以下Davey-Stewartson I方程的2组非平凡解:
情形3当λ2-4μ<0时,
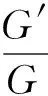
(32)

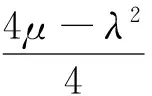
(33)
将式(13),式(14),式(19),式(20),式(32)和式(33)代入式(7),可得以下Davey-Stewartson I方程的2组非平凡解:
为了研究Davey-Stewartson I方程解的性质,下面给出方程部分解的函数图像.
当α=1,β=1,γ=1,δ=2,ζ=1,ω=1,r=1,λ=5,μ=4,y=1,C1=1,C2=2时,式(30)的函数图像如图1所示.

图1 式(30)的函数图像 图2 式(34)的函数图像
当α=1,β=1,γ=1,δ=1,ζ=0,ω=1,r=2,λ=0,μ=1,y=1,C1=1,C2=1时,式(34)的函数图像如图2所示.
3 结 语
本文应用G′/G展开法成功地求出了Davey-Stewartson I方程的9组精确解,并对解的性质作了简单的分析.但是,对于诸如积分形式的(2+1)维Sawaka-Kotera方程[13]
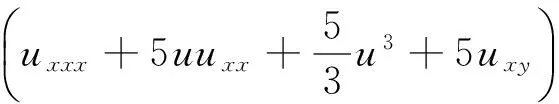
是否也能够用此方法进行求解,作者将作更深入的研究.
[1]范恩贵,张鸿庆.Whitham-Broer-Kaup浅水波方程的Bäcklund变换和精确解[J].应用数学和力学,1998,19(18):667-670.
[2]朱佐农.若干非线性偏微分方程的Painlevé性质和Bäcklund变换[J].东南大学学报:自然科学版,1994,24(2):132-136.
[3]范恩贵,张鸿庆.齐次平衡法若干新的应用[J].数学物理学报,1999,19(3):286-292.
[4]李德生,张鸿庆.改进的tanh函数方法与广义变系数KdV和MKdV方程新的精确解[J].物理学报,2003,52(7):1569-1573.
[5]徐桂琼,李志斌.构造非线性发展方程孤波解的混合指数方法[J].物理学报,2002,51(5):946-950.
[6]张大军,邓淑芳,陈登远.mKdV-Sine-Gordon方程的多孤子解[J].数学物理学报,2004,24A(3):257-264.
[7]阮航宇,陈一新.(2+1)维非线性薛定谔方程的环孤子,dromion,呼吸子和瞬子[J].物理学报,2001,50(4):586-592.
[8]蔡国梁,张风云,任磊.用扩展的F-展开法求耦合Schrödinger-Boussinesq方程组的精确解[J].应用数学,2008,21(1):90-97.
[9]智红燕,陈勇,张鸿庆.广义射影Riccati方程方法与(2+l)维色散长波方程新的精确行波解[J].数学物理学报,2005,25A(7):956-964.
[10]何宝钢,徐昌智,张解放.扩展的形变映射方法和(2+1)维破裂孤子方程的新解[J].物理学报,2006,55(2):511-516.
[11]李帮庆,马玉兰.(G′/G)展开法和(2+1)维非对称Nizhnik-Novikov-Veselov系统的新精确解[J].物理学报,2009,58(7):4373-4378.
[12]张金良.Davey-Stewartson I的周期波解[J].数学物理学报,2005,25A(2):213-219.
[13]阮航宇.(2+1)维Sawada-Kotera方程中两个Y周期孤子的相互作用[J].物理学报,2004,53(6):1617-1622.
SeekingforexactsolutionsforDavey-StewartsonIequationwithG′/G-expansionmethod
FENG Qingjiang
(CollegeofMathematicsandScience,KaiLiUniversity,KaiLiGuizhou556000,China)
By usingG′/G-expansion method, it was obtained the exact solutions for Davey-Stewartson I equation, the properties of solutions was also analysed.
G′/G-expansion method; complex coefficient; Davey-Stewartson I equation; the exact solutions
2012-04-21
贵州省凯里学院教学团队资助项目(JXTD201101);贵州省凯里学院校级课题(Z1219)
冯庆江(1981-),男,河北秦皇岛市人,助教.研究方向:孤立子理论与可积系统.
O175.2
A
(责任编辑 陶立方)
