弱L-平均条件下非精确牛顿型迭代法的半局部收敛性
2012-11-07徐秀斌
刘 涛, 徐秀斌, 肖 媛
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
1001-5051(2012)04-0395-06
弱L-平均条件下非精确牛顿型迭代法的半局部收敛性
刘 涛, 徐秀斌, 肖 媛
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
主要研究了在弱L-平均条件下非精确牛顿型迭代法在求解非线性算子方程时的半局部收敛性.这种弱L-平均条件包含了常用的Lipschitz条件作为特殊情形,故所得收敛结果具有一般性.
非线性算子方程;非精确牛顿型迭代法;半局部收敛;弱L-平均条件
0 引 言
令X和Y是欧氏空间或一般的Banach空间,D是X的一个开凸子集,设F:D⊂X→Y是一个Fréchet可导的非线性算子,
求解非线性方程(1)的近似解是一个重要的问题,因为大量的不同类型的实际问题都可归结为方程(1)的形式,如微分方程、边界值问题、积分方程等.常常用非精确迭代程序求方程(1)解的问题,它的一般表达形式为
式(2)中:初始点x0给定;在Rn中A(xk)是一个n×n的非奇异矩阵;控制序列{ηk}满足0≤ηk≤1.当A(xk)=F′(xk)时,可以得到非精确牛顿型迭代法,其迭代程序为
当A(xk)=F′(x0)时,可以得到简化的非精确牛顿迭代法;当A(xk)近似于F′(xk)时,就得到了非精确牛顿型迭代法(2)[1].
非精确牛顿迭代法包含了经典的牛顿迭代法[2-3],对于非精确牛顿法残余序列的选择影响着非精确牛顿法的收敛性.文献[4]给出了非精确牛顿法(3)的半局部收敛定理,其中残余序列{rn}满足:

此时0≤ηn<η< 1.文献[5]利用Lipschitz条件在开集B(x0,δ)上给出了非精确牛顿迭代法(3)的半局部收敛定理,此时{rn}满足
‖F′(x0)-1rn‖≤ηn‖F′(x0)-1F(xn)‖1+β,0≤β<1.
文献[6]利用Hölder条件,在集合B(x0,r)上给出了非精确牛顿迭代法(3)的半局部收敛定理.文献[7]利用局部弱L-平均条件

在集合B(x0,δ)上给出了非精确牛顿迭代法(3)的局部收敛定理.其中:ρ(x)=‖x-x*‖;xτ=x*+τ(x-x*)(0<τ<1).文献[8]利用弱L-平均条件


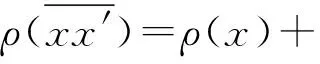
本文主要通过利用弱L-平均条件和控制条件‖F′(x0)-1(rn-rn-1)‖≤ηn‖xn-xn-1‖研究非精确牛顿型迭代法(2)的半局部收敛性,所得结果比文献[4,9]的相关结论更具有一般性.
1 引 理
根据本文的需要,首先给出4个引理及证明,然后在这些引理的基础上证明迭代方法(2)的半局部收敛性.

在给出收敛定理之前先定义如下2个辅助函数:


式(4)和式(5)中,L(u)为非负非减可积的连续函数.
函数f(x)和g(x)的导函数分别为:


则由式(6)和式(7)可以得到
取θ0>0,使得

且记

f(0)=β>0,f(θ0)=-ω2b+β<0,f(R)=β+λR>0.
故f在定义域[0,R]内恰有2个正根,分别记为t*和t**,且有
0 证明 由式(4)知 又由前面给出的条件易得f′(0)<0,f′(θ0)=0,f′(R)>0,故可以得到函数f(t)在区间[0,θ0]上单调递减,在区间[θ0,R]上单调递增;又因f(θ0)=-ω2b+β<0,故f在区间[0,R]内恰有2个正根t*和t**,所以有0 引理2设迭代序列 式(11)中,f(t),g(t)由式(4)和式(5)定义.设t*是方程f(t)=0在区间[0,θ0]的一个根,则由式(11)产生的序列{tn}有 且{tn}单调递增收敛到t*,并有 证明 由式(11)可得 下证t1 因此由f的单调性可知t1=β 现在假设t1 另一方面,由式(8)可以得到 所以式(12)得证.序列{tn}单调递增地收敛于一点,记为γ(γ∈[0,t*]),且γ也是方程f(t)=0的一个根.又由于t*是方程f(t)=0在[0,t*]内唯一的一个根,所以γ=t*,即序列{tn}收敛到t*. 最后证明式(13)成立.由式(8)可以得到 故式(13)成立.引理2证毕. 引理3假设F′(x0)-1F′在开域B(x0,t*)上满足 且对于任意x∈B(x0,t*),F′(x)-1存在,则 证明 由已知可得 则由Banach引理和式(9)易得 故式(18)成立.引理3证毕. 引理4[3]设 其中0≤ρ≤t*,且L(u)在[0,t*]上非负递增,则φ(t)在[0,t*-ρ]上关于t单调递增. 根据上面的引理,以下给出非精确牛顿型迭代法(2)的半局部收敛性定理. 定理1假设F:D⊂X→Y是一阶连续Fréchet可导的非线性算子,D是X的开凸子集.若存在初始点x0∈D,使得F′(x0)-1∈L(Y,X)存在,且有: A(x)可逆;‖F′(x0)-1(A(x)-F′(x))‖≤ω1;‖A(x)-1F′(x)‖≤ω2. 证明 由非精确牛顿型迭代法的迭代式(2)可以得到 xn+1-xn=-A(xn)-1F(xn)+A(xn)-1rn,n=0,1,…, 所以 ‖xn+1-xn‖= ‖A(xn)-1(F(xn)-rn)‖≤ ‖A(xn)-1F′(xn)‖‖F′(xn)-1F′(x0)‖‖F′(x0)-1(F(xn)-rn)‖. (25) 下面用数学归纳法证明式(23)和 成立. 当k=0时,由式(20)有 ‖x1-x0‖=‖A(x0)-1(F(x0)-r0)‖≤β=t1-t0,t0=0. ‖z-x0‖≤‖z-x1‖+‖x1-x0‖≤t*-t1+t1-t0=t*-t0, 下面假设当k=n-1时结论成立,即有 其中:xn-1+τ=xn-1+τ(xn-xn-1);0<τ<1.所以由式(21)和式(22)及引理4有 (27) 所以由引理2、引理3及式(25)有 (28) ‖z-xn‖≤‖z-xn+1‖+‖xn+1-xn‖≤t*-tn+1+tn+1-tn=t*-tn. 根据定理1,当A(x)=F′(x)时,可以给出非精确牛顿迭代法(3)的半局部收敛性定理.此时优函数式(4)和式(5)为如下形式: (29) 定理2假设F:D⊂X→Y是一阶连续Fréchet可导的非线性算子,D是X的开凸子集.若存在初始点x0∈D,使得F′(x0)-1∈L(Y,X) 存在,且有 (31) (32) (33) 式(34)和式(35)中,{sn}单调递增收敛到s*并满足 当令L(u)≡L(这里L是一个大于零的常数)时,由定理2可以得到文献[4,9]中的相关结论. 推论1设F:D⊂X→Y在集合B(x0,t*)内连续可导,假设式(22)成立且控制序列{ηk}满足0≤ηk<1.F′(x0)F′满足对于任意的x∈B(x0,t*),‖x-x0‖+‖x-x′‖≤t*时有 ‖F′(x0)(F′(x)-F′(x′))‖≤L‖x-x′‖. 若2βL≤(1-η)2,则由迭代方法(3)产生的序列{xk}收敛到方程(1)的解x*. [1]Dembtexto R S,Eisenstat S C,Steihaug T.Inexact Newton methods[J].Numer Anal,1982,19(2):400-408. [2]Kantorvich L V,Akilov G P.Functional analysis[M].Oxford:Pergamon Press,1982. [3]Wang Xinghua.Convergence of Newton′s method and inverse function theorem in Banach space[J].Math Comput,1999,68(225):169-186. [4]Guo Xueping.On semilocal convergence of inexact Newton methods[J].Comput Math,2007,25(2):231-242. [5]Argyros I K,Ren Hongmin.Kantorovich-type semilocal convergence analysis for inexact Newton methods[J].Comput Appl Math,2011,235(9):2993-3005. [6]Shen Weiping,Li Chong.Convergence criterion of inexact Newton methods for operators with Hölder continuous derivatives[J].Taiwanese Journal of Math,2008,12(7):1865-1882. [7]Chen Jinhai,Li Weiguo.Convergence behaviour of inexact Newton methods under weak Lipschitz condition[J].Comput Appl Math,2006,191(5):143-164. [8]Wu Min.A new semilocal convergence theorem for the inexact Newton methods[J].Appl Math Comput,2008,200(1):80-86. [9]Argyros I K.On the semilocal convergence of inexact Newton methods in Banach spaces[J].Comput Appl Math,2009,228(9):434-443. SemilocalconvergenceofinexactNewton-typeiterationmethodsunderweakL-averagecondition LIU Tao, XU Xiubin, XIAO Yuan (CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China) The semilocal convergence properties of the variants of inexact Newton-type iteration methods for nonlinear operator equations were studied under the hypothesis that the first derivative satisfies weakL-average conditions. These conditions included the usual Lipschitz condition as special cases. nonlinear operator equations; inexact Newton-type iteration method; semilocal convergence; weakL-average condition 2012-04-10 刘 涛(1987-),男,河南固始人,硕士研究生.研究方向:非线性数值逼近. O241 A (责任编辑 陶立方)


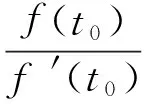





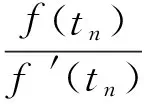






2 半局部收敛性定理



















3 应 用










