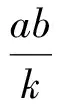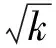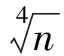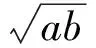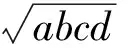与等式ab=cd相关联的竞赛题

●

(南京师范大学 江苏南京 210000)

与等式ab=cd相关联的竞赛题

●葛军

(南京师范大学 江苏南京 210000)

有一系列的竞赛题均涉及到等式的理解和运用.现举例加以说明.

结论1设a,b,c,d为正整数，满足ab=cd，则必存在正整数r,s,u,v，且(r,s)=1，使得a,b,c,d分别可以表示为a=ru，b=sv，c=su，d=rv.

利用结论1，可以较容易地解决一些竞赛题.

例1设a,b,c,d为正整数，满足ab=cd，求证：a2+b2+c2+d2是合数.

分析由结论1，得

a2+b2+c2+d2=

(ru)2+(su)2+(sv)2+(rv)2=

(r2u2+r2v2)+(s2v2+s2u2)=

(r2+s2)(u2+v2).

由a,b,c,d为正整数，知r,s,u,v是正整数,因此

u2+v2≥12+12=2，

同理

r2+s2≥2,

从而可得a2+b2+c2+d2为合数.

评注该题是美国的一道竞赛题.题目虽解答完毕，但还需追求“一分钟的过程，必获十分钟的效果”.首先，可以反思总结出：解决因数分解问题的基本思路之一，就是转化为因式分解问题来处理.其次，自然地运用“一般化”意识,心问：当满足例1的条件时，an+bn+cn+dn(n≥1,n∈N+)仍是合数吗？在a2+b2+c2+d2的分解中，可以将各项式子一般化，即

an+bn+cn+dn=

(rnun+rnvn)+(snvn+snun)=

(rn+sn)(un+vn)

也为合数.

特别地，当n=1时的结论还可以参见文献[1].另外，根据上述过程还可以得到:

a2+b2-c2-d2=

(ru)2+(su)2-(sv)2-(rv)2=

(r2-s2)(u2-v2)=

(r-s)(u-v)(r+s)(u+v).

例2设a,b,c,d为正整数，满足ab=cd，a+b=c-d，求证：存在边长是整数且面积为ab的直角三角形[2].

分析本题的题意是要求证明：存在正整数x,y，使得xy=2ab，且x2+y2为完全平方数.由ab=cd及结论1，可令a=mu,b=nv，c=nu,d=mv,代入a+b=c-d，得

a+b+c+d=2c，

即

(m+n)(u+v)=2c.

对照2ab=2cd，自然地考虑尝试在等式的2边同乘以d(即mv)，得

(m+n)(u+v)·mv=2c·mv=2cd=2ab,

从而 [(m+n)v] [(u+v)m]=

(mv+nv)(mu+nv)=2ab,

即

(d+b)(d+a)=2ab.

假若可以验证(d+a)2+(d+b)2为完全平方数，则问题得到解决.事实上，

(d+a)2+ (d+b)2=

2d2+2d(a+b)+a2+b2=

2d(d+a+b)+a2+b2=

2dc+a2+b2=(a+b)2,

故例2得证.

评注注意到ab=cd及a+b=c-d，联想到a,b为一个一元二次方程的2个根，于是例2变形为2012年全国高中数学联赛江苏赛区初赛试题：

设a,b,c,d为正整数，a,b为方程x2-(d-c)x+cd=0的2个根，证明：一定存在边长是整数且面积为ab的直角三角形.

(第26届独联体数学奥林匹克竞赛试题)

分析观察题中条件与结论，注意到k可视为不变量，尝试从n-k与k的大小关系入手.由k

kn=lm=(k+a)(k+b)=k2+(a+b)k+ab,

推得k|ab，从而ab≥k.因此,

前面讨论了基于直接给出等式ad=bc的相关问题的解决，下面给出2个例题，需先揭示出等式ad=bc，然后再证明问题的结论.

例4在2个相邻的完全平方数n2与(n+1)2之间任取若干个不同的整数，证明：它们中两两乘积互不相同.

(第17届全苏数学奥林匹克竞赛试题)

分析若取2个数，则无两两乘积，不符题意.若取3个数a,b,c,不妨设a

ab

但ad与bc的大小不定，于是就需考虑ad≠bc是否成立？ 考虑到4个数是任取的，则取多于4个数的情况，就可以转化为任取4个数的问题，即探究在任取的4个数中，两两乘积是否不相同.于是，问题就转化为证明：

对于给定的正整数n，若正整数a,b,c,d满足n2

采用反证法证明.假设存在a,b,c,d且n2

a=ru,b=su,c=rv,d=sv,(u,v)=1.

由b>a，c>a，得s>r,v>u，即有

s≥r+1,v≥u+1，

从而

d=sv≥(r+1)(u+1)=ru+(r+u)+1,

而(n+1)2>d，矛盾.

因此，对于介于n2与(n+1)2之间的任意4个整数，它们的两两乘积互不相同，即例4得证.

评注反思上述的证明思路，条件n2

若r≠u，则

在上述推导过程中,

结论成立.

若r=u，则由b

d=sv≥(s+1)s≥(r+2)(r+1)>r2+2r+1.

因为r=u，a=ru≥n2，所以r=u≥n.于是

d=sv>r2+2r+1≥n2+2n+1=(n+1)2,

这与d≤(n+1)2矛盾.

因此，进一步地，得到命题：

命题1对于给定的正整数n，若正整数a,b,c,d满足n2≤a

与例4相比，证明该命题的复杂之处就是需要分情形讨论，其难度也就加大了.例4还可以变化为：

对于给定正整数n，一定存在2n+2个连续整数，使得任取其中若干个数，两两乘积都不相同.

分析遇到唯一性问题，常用反证法来处理.

假设n的分解不是唯一的，则n还可分解为n=u′v′，即uv=u′v′.由uv,u-v联想到

(u-v)2=u2-2uv+v2，

同理可得

(u′-v′)2=u′2-2u′v′+v′2.

由uv=u′v′及结论1，可令u=ac，v=bd，u′=bc,v′=ad，(c,d)=1，这里a,b,c,d为正整数.于是

(u-v)2- (u′-v′)2=u2+v2-u′2-v′2=

(ac)2+(bd)2-(bc)2-(ad)2=

(a2-b2)(c2-d2)=

(a-b)(c-d)(a+b)(c+d).

假设u-v≠u′-v′，则由n为奇数得u,v,u′,v′均为奇数，从而a,b,c,d也均为奇数.若a-b>0,c-d>0，则a-b>2,c-d>2，从而

(u-v)2-(u′-v′)2=

(a-b)(c-d)(a+b)(c+d)≥

2·2·(a+b)·(c+d)>

(1)

这与式(1)矛盾.

假设u-v=u′-v′，即u-u′=v-v′.若u>u′，则v-v′>0，得v>v′，因此n=uv>u′v′=n，矛盾.同理若uu′-v′，即

而 (u-v)2-(u′-v′)2=

(a-b)(c-d)(a+b)(c+d)>0,

(3)

由式(2)，(3)得a>b，c>d.例5得证.

在解决竞赛问题时，首先要学会从简单入手，竞赛题的难度就在于对基本知识熟悉的程度和对简单知识理解的程度.越深刻越本质的知识是竞赛必测的.其次，要学会运用基本的逻辑证明方法(如反证法)处理问题.再次，学会运用“一般化”意识，对所要处理的或已处理的问题进行反思.最后，不要忽视书写的规范，本文期许读者能够简捷、完整地书写上述各例的解答过程.若然，你就会对解题思路有更深刻的认识，甚至得到更为简捷的其他做法以及挖掘出相关的系列问题.如反思例1，你会认识到另外2个解题方向：4个数的平方和可否表示为2个平方数的和、可以表示为2个数平方和的数之积也可以表示为2个数的平方和，自然地再考虑更为一般的问题，如此下去，就会联想到一些著名的数学问题.

[1] 王志雄.数学奥林匹克竞赛36计[M].北京：电子工业出版社,1993.

[2] 余红兵.数学竞赛中的数论问题[M].上海：华东师范大学出版社，2005.