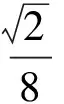竞赛中的数列题评析

●

(东阳中学 浙江东阳 322100)

竞赛中的数列题评析

●陈硕罡

(东阳中学 浙江东阳 322100)

全国高中数学联赛经过20多年的发展，虽然试题题型等几番变化，但总体形成了自己特定的命题风格，特别是一些重点内容，可以说是“年年必考、常考常新”.数列就是这样的一个内容，它在整个中学数学教学中处于一个知识汇合点的地位，很多知识都与数列有着密切的联系.不少关于恒等变形、解方程组、解不等式以及一些带有综合性的数学问题都与数列有关，通过数列能考查学生的综合思维能力和综合运用知识解决问题的能力，因此数列一直受到命题者的青睐.本文将在分析2006～2011年全国高中数学联赛数列试题的基础上，提出数列内容备考的若干思考和建议，与同仁们探讨.

1 近6年全国高中数学联赛数列试题回顾

表1 近6年的数列试题

从表1中，我们可以归纳出全国高中数学联赛对数列内容考查的2个特点：(1)在客观题中，以考查等差数列和等比数列的概念和性质为主，同时结合函数、不等式、数论等知识进行考查，难度相对稳定；(2)在主观题中，基本上都是考查由数列的递推公式求数列的通项公式，然后判断数列的性质或对其求和，或结合其他知识点如存在性问题、唯一性问题等进行考查.对数列而言，求数列的通项是解决数列问题的关键，同时这也是解决数列问题的难点所在.

2 数列试题评析及备考建议

分析历年全国联赛试题的目的不是要押题猜题，而是要分析竞赛试题的特点，把握竞赛命题的方向，寻求竞赛备考的对策.笔者认为，解决数列问题的核心是求数列的通项公式，可以说数列的通项是数列问题的生命线.纵观近几年的联赛数列试题，最终往往是通过构造等比或等差模型来解决.掌握构造的常见技巧和结论，根据递推公式构造等差、等比数列，是解决问题的难点所在.

2.1 特征根法求通项

例1已知p,q(q≠0)是实数，方程x2-px+q=0有2个实根α，β，数列{an}满足a1=p，a2=p2-q，an=pan-1-qan-2(n=3,4,…).

(1)求数列{an}的通项公式(用α，β表示)；

(2009年全国高中数学联赛试题)

解(1)由韦达定理知αβ=q≠0，又α+β=p，因此a1=α+β,a2=α2+β2+αβ,特征方程λ2-pλ+q=0的2个根为α，β．

①当α=β≠0时，通项an=(A1+A2n)αn(n=1,2,…)，由a1=2α，a2=3α2得

解得A1=A2=1,故an=(1+n)αn.

②当α≠β时，通项an=A1αn+A2βn(n=1,2,…),由a1=α+β，a2=α2+β2+αβ得

(2)略.

评析数列的递推关系形如an+1=pan+qan-1(n≥2,pq≠0)，其特征方程为x2=px+q，α,β为特征根.(1)若α≠β，则其通项an=Aαn+Bβn；(2)若α=β，则其通项an=(A+Bn)αn-1(式中A，B由初始值a1,a2确定).

2．2 待定系数法求通项

例2一个由若干行数字组成的数表，从第2行起每一行中的数字均等于其肩上的2个数之和，最后一行仅有一个数，第一行是前100个正整数按从小到大排成的行，则最后一行的数是______(可以用指数表示).

(2009年全国高中数学联赛试题)

解(1)易知：该数表共有100行；

(2)每一行构成一个等差数列，且公差依次为d1=1,d2=2,d3=22,…,d99=298;

(3)a100为所求．

设第n(n≥2)行的第一个数为an，则an=2an-1+2n-2，两边同除2n可得

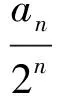
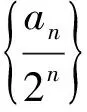
评析数列的递推关系形如an=pan-1+qrn，往往可变形转化为

这样就构造了一个等比数列，从而求得所需的通项公式.

2.3 不动点法求通项

(1)对于怎样的实数x与y，总存在正整数n0，使当n0≥n时，an恒为常数？

(2)求数列{an}的通项公式.

(2006年全国高中数学联赛加试试题)

由此递推，可得

这里Fn=Fn-1+Fn-2(n≥2)，F0=F1=1.由特征根法(或直接由斐波那契数列的通项公式)得

上式中的n还可以负向延伸，例如F-1=0，F-2=1.这样，通项公式对所有的n≥0都成立，因此

x2-2px+q=0.

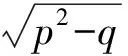
其中{Fn}为斐波那契数列，由此可求得数列{an}的通项公式.

对数列问题而言，求通项公式是关键.中学阶段常见的是等比模型和等差模型，因此不论碰到什么样的题目，都要通过对递推公式进行化简变形.在这个过程中需要掌握一些常见的结论和固定的变形技巧，在不断尝试探索的过程中，完成构造等比数列模型和等差数列模型，从而化未知为已知，实现问题的解决.

同步练习

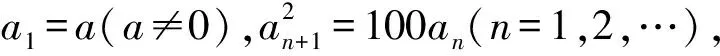
4.已知数列{an}(n≥0)满足a0=0，a1=1，对于所有正整数n，有an+1=2an+2 007an-1，求使得2 008|an成立的最小正整数n.

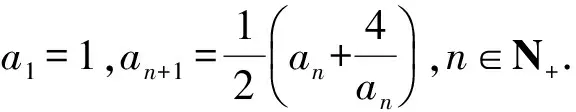
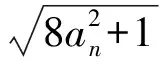
参考答案

1.解由题意得an>0，对递推式2边取对数得

2lgan+1=lgan+2.

由特征根法可求得

易得

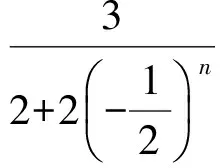
从而

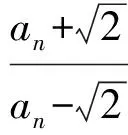
于是

4.解设m=2 008，则an+1=2an+2 007an-1的特征方程为

λ2-2λ-2 007=0，

由二项式定理得

5.解由递推关系知其不动点为2和-2，则

6.解由原递推式可得

展开可得

同理

两式相减，可得

即

an+1+an-1=6an，

由特征根法易求