一道自主招生题的引申
2012-11-07
●
(中国科技技术大学 安徽合肥 230026)
一道自主招生题的引申
●王建伟
(中国科技技术大学 安徽合肥 230026)
例1设a,b为实数,已知对任意实数x,有acosx+bcos2x≥-1恒成立,求a+b的最大值.
(2009年北京大学自主招生数学试题)

例2设a,b为实数,已知对任意实数x,有acosx+bcos2x≥-1恒成立.
(1)求a+b的最大值,及取得最大值的所有数对(a,b);
(2)求a+b的最小值,及取得最小值的所有数对(a,b).

f(t)=2bt2+(2-b)t+(1-b),

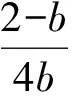
Δ= (2-b)2-4×2b×(1-b)=
9b2-12b+4=(3b-2)2≤0,

(2)取x=0,得a+b≥-1.若a+b=-1,则a=-b-1.令t=cosx,则-1≤t≤1.记
g(t)=2bt2-(b+1)t+(1-b),
条件转化为:当-1≤t≤1时,g(t)≥0恒成立.特别地,g(-1)=2+2b≥0,故b≥-1.
若-1≤b≤0,则g(t)是开口向下的二次函数,最小值必可在某端点取得,而g(1)=0,g(-1)≥0,这样的b必满足要求.
若b=0,则g(t)=-t+1为减函数,而g(1)=0,则b=0也满足要求.


Δ= (b+1)2-4×2b×(1-b)=
9b2-6b+1=(3b-1)2>0,
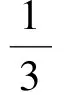
例3设a,b,c为实数,f(x)=acosx+bcos2x+ccos3x.已知对任意实数x,有f(x)≥-1恒成立,求a+b+c的最大值,及取得最大值的所有数组(a,b,c).

-a+b-c≥-1,
于是
a+c≤1+b≤2,
从而
a+b+c≤1+2=3.
若a+b+c=3,则b=1,a+c=2.此时,令t=cosx∈[-1,1],则
(2-c)t+2t2-1+c(4t3-3t)≥-1,
即
t(2ct2+t+1-2c)≥0.
当0 1-2c=0, 解得 例4设a,b为实数,已知对任意实数x,有acosx+bcos3x≥-1恒成立,求b的最大值和最小值. 解取x=0,得 a+b≥-1. (1) 即 -a+2b≥-2. (2) 式(1)+式(2),得 3b≥-3, 故 b≥-1. 例5设a,b,c为实数,已知对任意实数x,有acosx+bsinx+ccos3x≥-1恒成立,求c的最大值和最小值. 解先证明一个引理. 引理1 (引理的证明可用和差化积或复数的方法,略.) 记f(x)=acosx+bsinx+ccos3x,由引理1,得 分别取x=0和x=π,得-1≤c≤1.另外,易知(a,b,c)=(0,0,1)和(a,b,c)=(0,0,-1)满足要求,因此c的最大值为1,最小值为-1. 最后给出一个更一般的问题,细细品味我们可以了解问题的本质. 例6设a1,a2,…,an,b1,b2,…,bn,c为实数.记f(x)=a1cosx+b1sinx+…+ancosnx+bnsinnx+ccos(n+1)x,已知对任意实数x,有f(x)≥-1恒成立,求c的最大值和最小值. 解先证明一个引理. 引理2设m,n为正整数,m≤n,且x为实数,则 引理2的证明 由此立得. (不熟悉复数的读者可用和差化积及裂项求和的方法证明,略.) 由引理2,得 (n+1) ·c·cos(n+1)x=