巧用正三角形解题
2012-11-07
●
(余姚市实验学校 浙江余姚 315400)
巧用正三角形解题
●应立君余雪赞
(余姚市实验学校 浙江余姚 315400)
正三角形又称等边三角形,是最完美的三角形.它的3条边相等,3个内角均为60°,可以据此进行边角的传递、转化;它是轴对称图形,被对称轴分成的2个三角形(含有30°角的特殊直角三角形),可以据此进行长度、角度、面积等计算;它又是旋转对称图形,据此可把它分成3个全等的特殊等腰三角形(顶角为120°).本文介绍正三角形在竞赛解题中的的几种用法,旨在抛砖引玉.
1 化归成“正三角形”
正三角形是特殊的锐角三角形,据此可以对某些试题进行特殊化求解.
例1已知锐角△ABC的顶点A到垂心H的距离等于它的外接圆的半径,则∠A的度数是
( )
A.30° B.45° C.60° D.75°
(2007年全国初中数学联赛试题)
原解如图1,联结BO并延长交⊙O于点A′,联结AA′,A′C.易知AH⊥BC,A′C⊥BC,得
AH∥A′C,
同理
AA′∥HC,
因此

得∠BA′C=60°,故∠BAC=60°.
巧解联想到△ABC为正三角形时,正好满足题设条件.故选C.
评注针对单项选择题,若用特殊值法,则可快速高效地解决.
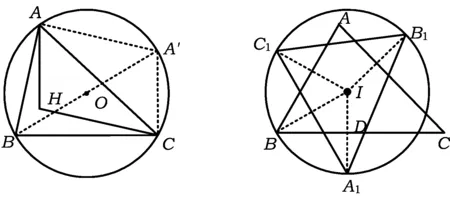
图1 图2
例2已知点I是锐角△ABC的内心,A1,B1,C1分别是点I关于边BC,CA,AB的对称点.若点B在△A1B1C1的外接圆上,则∠ABC=
( )
A.30° B.45° C.60° D.90°
(2005年全国初中数学联赛试题)
原解如图2,联结IA1,IB1,IC1,IB.由轴对称性知
IA1=IB1=IC1=2ID,
且ID⊥BC,点I是△A1B1C1的外心,因此IB=2ID,从而∠IBD=30°.同理∠IBA=30°,于是∠ABC=60°.故选C.
巧解当△ABC为正三角形时,满足题设条件.故选C.
评注利用正三角形内心、外心重合的特殊性质,联想到正三角形与之契合.
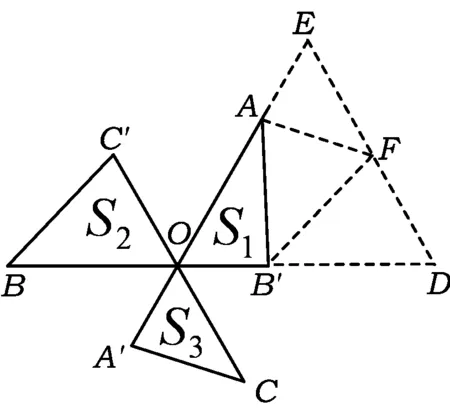
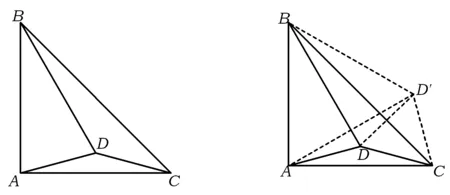
例3已知正数a,b,c,A,B,C满足a+A=b+B=c+C=k.求证:aB+bC+cA (第21届全苏数学奥林匹克竞赛试题) 原解设f(a)=aB+bC+cA-k2= a(k-b)+b(k-c)+c(k-a)-k2= (k-b-c)a+(b-k)(k-c), 当k-b-c=0时,f(a)=(b-k)(k-c)<0;当k-b-c≠0时,f(a)是a关于的一次函数,f(a)随着a的变化而单调增加或减少,且 f(0)=(b-k)(k-c)<0, f(k)=k(k-b-c)+(b-k)(k-c)=-bc<0. 因此,当0 aB+bC+cA-k2<0, 故 aB+bC+cA 图3 图4 巧解如图3,构造边长为k的正△PQR,在各边上分别取点D,E,F,使PD=A,QE=B,RF=C,则QD=a,RE=b,PF=c.易知 S△QDE+S△REF+S△PFD 得 即 aB+bC+cA 评注原解构造函数的代数解法不易想到,做起来也比较困难.若能拓展思路,大胆创新,联想到正三角形的性质,运用面积关系进行整体上的把握,便简洁明了. 平面几何竞赛题,总给人难以入手的感觉,究其原因是图形识别存在障碍,特别是有些问题的图形不完整,让人“不识庐山真面目”.解决此类问题需要大胆想象,积极尝试,填补缺陷,创造完美.正三角形的多重特性,使其成为联想的重要对象. 例4在△ABC中,已知∠CAB=60°,点D,E分别在边AB,AC上,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB= ( ) A.15° B.20° C.25° D.30° (2010年全国初中数学联赛试题) 解如图4,延长AB到点F,使BF=AD.先证△ADE与△ACF均为正三角形,从而 AC=CF,∠A=∠F=60°,AD=BF, 因此△ADC≌△FBC,得CD=CB.再求 从而∠DCB=20°.故选B. 评注根据已知条件,补画正三角形,使整个图形成轴对称,容易作出恰当的判断,反复运用正三角形3条边相等、3个内角为60°的性质,完整地推理出结论. 图5 (第20届希望杯全国数学邀请赛初中试题) 评注若用代数方法分别计算S1,S2,S3,则有繁琐之嫌.针对3条等长线段及两两夹角为60°的已知条件,通过平移构造正三角形,从整体上考虑,给人以耳目一新之感. 例6如图6,△ABC是等腰直角三角形,∠BAC=90°,D是△ABC内一点,且∠DAC=∠DCA=15°.求证:BD=BA. (2009年湖北省黄冈市初中数学竞赛试题) 图6 图7 证法1如图7,作点D关于BC的对称点D′,联结D′A,D′B,D′C,D′D.易知△DD′C为正三角形,可证明△ACD≌△AD′D,得 AD′=AC=AB,∠BAD′=60°, 从而△ABD′为正三角形,再证明BD=BA. 证法2如图8,以AD为边作正△ADE,联结BE.先证△ACD≌△ABE,得 ∠AEB=∠ADC=150°, 再证明△BAE≌△BDE,结论得证. 图8 图9 证法3如图9,延长CD交∠BAC的平分线于点F,联结BF.由轴对称性易证△ACF≌△ABF,得 ∠AFB=∠AFC=∠BFD=120°, 再证△BAF≌△BDF,得BA=BD. 评注注意到题中已知∠DCB=30°(由结论逆推可知∠ABD也为30°),因此通过轴对称变换可得证法1中的正△DCD′和△ABD′,顺着猜想,合情推理表达即可.另外,本题的解法很多,以任何一条线段为边作正三角形均可证明结论. 2个正三角形共顶点时,往往可以找到一对全等三角形(如图10,若△ABC与△DEC是正三角形,则必有△ACE≌△BCD,得BD=AE,且BD,AE的一个夹角为60°),解题时可以据此进行角、线段的等量代换. 图10 例7如图11,△ABC与△DEC均是等边三角形.若∠AEB=145°,则∠DBE的度数是________. (2012年全国初中数学联赛海南赛区试题) 解由已知可证△ACE≌△BCD,从而∠CAE=∠CBD.由凹四边形ACBE得 ∠AEB=∠EAC+∠EBC+∠ACB, 即 ∠EBD=∠AEB-∠ACB=145°-60°=85°. 评注这是由2个正三角形共顶点组成的基本图形,一定含有一对全等三角形,可以进行角度的转移,再结合正三角形的一个内角为60°的隐含条件,迅速准确地求出答案. 图11 图12 例8已知O是等边△ABC内的一点,∠AOB,∠BOC,∠AOC的角度之比为6∶5∶4.则在以OA,OB,OC为边的三角形中,此三角形所对的角度之比为________. (2005年山西省太原市初中数学竞赛试题) 解如图12,以AO为边作正△AOO′,联结O′C.易证△ABO≌△ACO′,得 CO′=BO, 由正△AOO′知AO=OO′,且 ∠AOO′=∠AO′O=60°, 因此△OO′C与以OA,OB,OC为边的三角形全等.可求得 ∠OO′C=144°-60°=84°, ∠OCO′=60°, 从而以OA,OB,OC为边的三角形的对应角度之比为60∶36∶84=5∶3∶7. 评注已有一个正三角形,再添一个正三角形与之共顶点,构成基本图形,实现角及边长的转移.再结合正三角形3条边相等,每个内角为60°的性质,解决问题. 例9已知点P是锐角△ABC内的一个点,且使PA+PB+PC最小.试确定点P的位置,并证明你的结论. (2009年天津市初中数学竞赛试题) 图13 图14 证明如图13,分别以AP,AC为边作正△APP′和正△AB′C,联结P′B′.先证△APC≌△AP′B′,得PC=P′B′.由正△APP′得AP=PP′,从而PA+PB+PC转化为BP+PP′+P′B′. 而对一个确定的锐角△ABC,点B与B′的相对位置关系是确定的,根据“两点之间线段最短”可知B,P,P′,B′在同一直线上时取得最小值(如图14).进而可以说明此时 ∠APB=∠APC=∠BPC=120°. 评注求3条呈发散状的线段和的最小值,往往需要转化成确定2个端点的折线长,而2个正三角形共顶点的基本图形恰能帮助实现这一目标. 本题结论实质上是著名的费马点问题的一部分,有兴趣的读者可以查阅相应的资料,作进一步研究.实践中确定点P的位置的作图方法可以是:以△ABC(最大内角小于120°)的2条边(如AB,AC)为边长,向外作正△ABC′与正△ACB′,线段BB′与CC′的交点就是所求的点P(若以BC为边向外作正△BCA′,则AA′必经过点P).

2 补形成“正三角形”

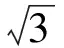
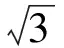

3 构造姐妹“正三角形组”