希望杯数学邀请赛九年级二试模拟试题
2012-11-07睿达资优教育命题组
希望杯数学邀请赛九年级二试模拟试题
一、选择题(共8小题,每小题5分,共40分)

( )
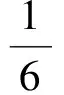
2.已知函数y=(1-a)x+a+4的图像不经过第四象限,则满足题意的整数a的个数有
( )
A.4个 B.5个 C.6个 D.无数个
3.十进制数是满十进位,二进制数是满二进位,三进制数是满三进位.十进制数234可写成1×27+1×26+1×25+0×24+1×23+0×22+1×21+0×20,因此234可记成二进制数为11 101 010.仿此把234记成三进制数应为
( )
A.22 002 B.20 022 C.22 202 D.22 200
4.△ABC的3条边长a,b,c均为整数,且a+bc+b+ca=24.当△ABC为等腰三角形时,它的面积数值不同答案的种数是
( )
A.2种 B.3种 C.4种 D.无数种
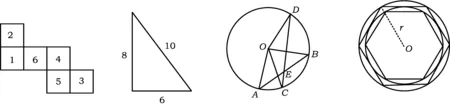
图1 图2 图3 图4
5.有一个边长为6,8,10的直角三角形(如图2),现要求拼上一个一条直角边为8的直角三角形,使拼成的三角形成为一个等腰三角形,则各种不同的拼法种数有
( )
A.无数种 B.4种 C.3种 D.2种
6.在一个停车场内有3类不同的车24辆,其中汽车有4个轮子,摩托车有3个轮子,自行车只有2个轮子.仔细数了一下,停车场内共有86个轮子.设3类车分别有x,y,z辆,那么满足条件的x,y,z的不同值的组数应该有
( )
A.2组 B.3组 C.4组 D.多于4组
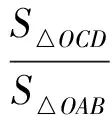
( )
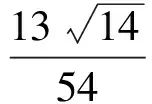
8.在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形(如图4),如此无限继续下去,那么所有这些圆面积之和会趋向于一个确定的常数,你猜想这个常数应该是
( )
A.2πr2B.3πr2C.4πr2D.5πr2
二、填空题(共8小题,每小题5分,共40分)
9.哥德巴赫猜想:任何一个不小于6的偶数可以写成2个奇素数之和.按这种要求表示126,则2个奇素数之间最大的差为______.
10.将1,2,3,…,49,50任意分成10组,每组5个数,每组中有1个中位数,则这10个中位数之和的最大值是______.
11.一个长方体的长、宽、高分别为9 cm,6 cm,5 cm.先从这个长方体上尽可能大地切下一个正方体,再从剩余部分上尽可能大地切下一个正方体,最后再从第2次的剩余部分上尽可能大地切下一个正方体,问经过3次切割后剩余部分的体积为______cm3.
12.用若干个相同的小立方体搭成一个几何体,使它的主视图和俯视图如图5所示.俯视图中小正方形中字母表示在该位置下方小立方体的个数,那么这个几何体最少由______个小立方体搭成,最多由______个小立方体搭成.
13.在矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图6放置,则矩形ABCD的周长为______.

图5 图6 图7
14.图7是4×4的正方形网格,以网格的格点(每个正方形的顶点称格点)为顶点的正方形一共有______个.
16.写出数列1,2,3,5,…的一个通项公式an=______.
三、解答题(共2小题,每小题20分,共40分)
17.在一个直角边为4的等腰直角△ABC(∠C为直角)中,剪出一块扇形,使扇形边缘的2条半径恰好都在△ABC的边上,且扇形的弧与△ABC的其他边相切.请画出所有可能符合题意的图形,并求出扇形半径.
18.已知函数y=(x-2)|x|,
(1)写出y随着自变量x的值增大而增大时,x的取值范围; 以及y随着自变量x的值增大而减小时,x的取值范围.
(2)当a<2时,求函数在a≤x≤2时的最大值和最小值.
参考答案
1.A 2.C 3.D 4.B 5.B 6.C 7.A 8.C
9.100 10.345 11.73 12.9,11
17.符合题意的图形如图8所示.

图8
18.(1)当x≤0时,y=-(x-1)2+1;
当x>0时,y=(x-1)2-1.
由图像可知,随着自变量x增大,y的值增大时x的范围是x≤0或x≥1;随着自变量x增大,y的值减小时x的范围是0≤x≤1.
(2)由函数当x≤2时的图像可知,ymax=0.
当1≤a<2时,ymin=a2-2a;


(供稿:睿达资优教育命题组)
