解决初中数学竞赛中杂题的常用策略
2012-11-07
●
(富阳市永兴中学 浙江富阳 311400)
解决初中数学竞赛中杂题的常用策略
●段春炳
(富阳市永兴中学 浙江富阳 311400)
数学竞赛中出现的杂题往往涉及数论、组合、图论等知识.这类问题背景丰富、解法灵活多变,而所涉及的知识和方法能体现数学的本质,能考查出学生数学思维的灵活性、深刻性和创造性,因而备受命题者的青睐.虽然这些题目没有固定的方法,但一些思想方法和数学原理常被用到,本文通过近几年的初中数学竞赛题举例说明.
1 用“抽屉原理”解决存在性问题
抽屉原理尽管很简单,却应用广泛,特别是在解决穷举有困难的存在性问题中,它往往能起到很好的效果.
例1有一系列数,前2个数是1,2,从第3个数起,每个数都等于它前面相邻的2个数的和的个位数字.请回答以下问题:
(1)在这列数中能否依次出现相邻的2,0,1,2这4个数?说明理由.
(2)这列数中的第2 012个数字是什么?说明理由.
(2012年希望杯初一数学竞赛第二试试题)
分析第(1)小题由奇偶性可知前2个数是偶数,则第3个数必为偶数,因此不可能出现2,0,1,2这4个数.
很多学生在解第(2)小题时一般能猜到这列数会出现循环,希望通过实验找出这个循环,但通过多次尝试没有出现循环时往往会否定自己开始的猜想,从而解题受阻.事实上求解此类试题的关键在于知道这列数是一定会循环的.
当相邻2个数重复出现时,数列就会出现循环,注意到这列数中只出现0到9的数字,因此不同的排列方式共有10×10=100种.因此,根据抽屉原理,相邻2个数在这无穷数串中必定会重复出现,此后成周期循环,且“最坏”的情况是直到第101、第102个数才与第1、第2个数重复.通过实验寻找,如表1所示.

表1 数表
从表1中可以发现,第61个数等于第1个数,第62个数等于第2个数,以下各数以60为周期循环出现.因为2 012=33×60+32,所以第2 012个数字等于第32个数字,即8.
2 用“不变量原理”解决操作性问题
有一类问题要求进行反复的操作,哪些结果可能出现,哪些结果不可能出现.解决此类问题的有效策略是:如果有重复操作,寻找操作过程中的不变量.
例2有3堆石子的个数分别为20,10,12,现进行如下操作:每次从3堆的任意2堆中分别取出1粒石子,然后把这2粒石子都加到另一堆上去.问:能否经过若干次这样的操作,使得
(1)3堆石子的石子数分别为4,14,24;
(2)3堆石子的石子数均为14.
若能满足要求,请用最少的操作次数完成;若不能满足,请说明理由.
(2010年城市杯初一数学应用能力决赛试题)
分析第(1)小题只要从20,10这2堆石子中连续取出6次都加到12这堆中,分别变为14,4,24,而且要得到4,最少是从10变到4,即最少要操作6次.
第(2)小题的答案是不可能满足要求的.将(a,b,c)变为(a-1,b-1,c+2),在这个操作的前后每2个数的差除以3的余数是不变的.3堆石子的石子数均为14,则两两的差除以3的余数均为0,这和起始状态不一致,因此不可能得到.
3 用“对应原理”解决计数问题
在很多复杂的计数问题中,当直接计数较为困难时,可以通过寻找对应关系间接计数.
例3如图1是4×4的正方形网格,以网格的格点(每个正方形的顶点称格点)为顶点的正方形一共有______个.

图1 图2
(第2届睿达杯七年级数学智能竞赛一试试题)
分析题中水平放置的正方形的个数容易得到,但不小心会忽视边与网线不平行的情况,且这种“斜放”的情况又不易计数.事实上由图2可知,这样“斜放”的每个正方形对应着一个水平放置的外接正方形.因此要对“斜放”的正方形进行计数,只要对水平放置的正方形进行计数即可,当然这里不是一对一的,一个边长为n的水平放置的正方形内接(n-1)个“斜放”的正方形,从而共有
16+9×(1+1)+4×(1+2)+1×(1+3)=50(个).
用这种方法可将问题推广到一般情形,即在n×n的正方形网格中可得到符合要求的正方形的个数有:
12×(1+n-1)+22×(1+n-2)+…+
(n-1)2×(1+1)+n2×(1+0)=
4 用“估计、构造”解决离散最值问题
对于离散最值问题,一般要从2个方面进行解答:一方面要“估计”出这个最值,另一方面要能“构造”出一个例子说明最值的存在.
例4有7个人进行某项目的循环比赛,每2个人恰好比赛一场,且没有平局.如果其中有3个人X,Y,Z,比赛结果为X胜Y,Y胜Z,Z胜X,那么我们称X,Y,Z构成一个圈.求在这7个人的比赛中,圈的数目的最大值.
(2008年全国初中数学联赛浙江赛区复赛试题)
分析可通过图形来表示题目的意思.如图3,若3个人A,B,C的比赛结果构成一个圈,则3个人胜负各一场,图中表现为“箭头一进一出”.如图4,若3个人A,B,C的比赛结果不能构成一个圈,则3个人中必有1人胜2场,1人负2场,图中表现为“箭头二出”与“箭头二进”.

图3 图4
在表示3个人比赛结果的胜负图中,把角两边“箭头一进一出”的角称为“好角”,角两边“箭头二出”或“箭头二进”的角称为“坏角”,那么当比赛结果构成圈时图中有3个“好角”(图3),不构成圈时有1个“好角”、2个“坏角”(图4).
设某个人胜k(k=0,1,2,3,4,5,6)场,则他负6-k场,可产生k(6-k)个“好角”.
当k=0,1,2,3,4,5,6时,
k(6-k)=0,5,8,9,8,5,0,
从而
k(6-k)≤9,
即每个人胜负构成的“好角”不超过9个.
再设7个人共构成n个圈,则“好角”共有3n+(35-n)个,由
3n+(35-n)≤9×7=63,
得
n≤14.
另一方面,14个圈是可能的.

因此,圈的数目的最大值为14.
5 用“极端原理”巧妙解题
在所研究的对象中如果存在最大或最小的对象,可以通过对它们的考查来发现问题的关键所在.考查问题的极端情形,往往能起到意想不到的效果,因为极端情形能很好地暴露出问题的矛盾.
例5如图5,在8个点处各写一个数字,已知每个点处所写的数字等于和这个点有线段相连的3个点处的数字的平均数,求代数式
的值.
(第13届希望杯全国数学邀请赛初二第二试试题)
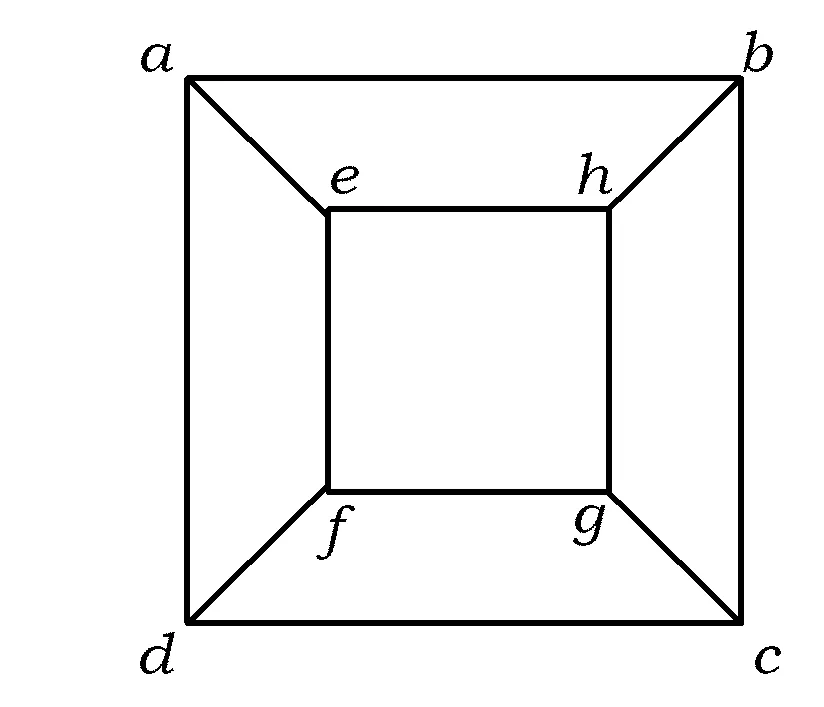
图5

a=b=d=e,
同理可得
c=f=g=h=a,
即
a=b=c=d=e=f=g=h,

[1] 恩格尔.解决问题的策略[M].舒五昌,冯志刚,译.上海:上海教育出版社,2001.
[2] 周春荔.初中数学竞赛中的思维方法[M].北京:中国物资出版社,2004.
