组合赛题解题思路的探索
2012-11-07
●
(南京市外国语学校 江苏南京 210008)
组合赛题解题思路的探索
●黄志军
(南京市外国语学校 江苏南京 210008)
组合赛题是国内外数学竞赛中的热点之一,是数学竞赛中难度较大的问题,同时也是考查学生数学思维的典型问题.组合问题的内容非常广泛,涉及到代数、几何、数论等多个分支,解法灵活多变.笔者选编了近几年国内外一些值得欣赏的典型赛题,并给出一些组合赛题的多种解法,以期灵活运用数学知识去进行探索与尝试,以展现思维的过程,尽力寻求更好的解法.
例1设空间中有2n(n≥2)个点,其中任何4个点都不共面,将它们之间任意连接N条线段,这些线段都至少构成一个三角形,求N的最小值.
分析通过构造实例,说明N≥n2+1,进而证明当N=n2+1时,若在2n个点间连有N条线段,则这些线段至少构成一个三角形.
解法1将2n个已知点均分为集合S和T:
S={A1,A2,…,An},T={B1,B2,…,Bn}.
现将每对点Ai和Bj之间都连接一条线段AiBj,而同组的任何2个点之间均不连线,则共有n2条线段.这时,2n个已知点中的任何3个点中至少有2个点属于同一集合,即这2个点之间没有连线.因而n2条线段不能构成任何三角形,这意味着N的最小值必大于n2.
下面用数学归纳法来证明:若在2n个已知点间连有n2+1条线段,则这些线段至少构成一个三角形.
当n=2时,n2+1=5,即4个点间有5条线段.显然,这5条线段恰构成2个三角形.设当n=k(k≥2)时命题成立,当n=k+1时,任取一条线段AB.若从点A,B向其余2k个点引出的线段条数之和不小于2k+1,则必定存在一点C,它与点A,B都有连线,从而△ABC即为所求.若从点A,B引出的线段条数之和不超过2k,则当把点A,B除去后,其余的2k个点之间至少还有k2+1条线段.由归纳假设知,它们至少构成一个三角形.
综上可知,所求N的最小值为n2+1.
解法2设这2n个点为A1,A2,…,A2n,可知所求N的最小值不小于n2+1.由于2n个点之间连有n2+1条线段,平均每个点引出n条线段还多,故可猜想必定有一条线段的2个端点引出的线段数之和不小于2n+1,用反证法证明.
设从A1,A2,…,A2n引出的线段条数分别为a1,a2,…,a2n且对于任一线段AiAj都有ai+aj≤2n.于是,所有线段的2个端点所引出的线段条数之和的总数不超过2n(n2+1).但在此计数中,点Ai恰被计算了ai次,故有

(1)
从而
(2)
式(2)与式(1)矛盾.从而证明了必有一条线段,从它的2个端点引出的线段数之和不小于2n+1.不妨设这条线段为A1A2,从而又有Ak(k≥3),使线段A1Ak,A2Ak都存在,于是△A1A2Ak即为所求.
解法3易知所求N的最小值不小于n2+1.下面用极端原理来证明,当N=n2+1时,这些线段至少构成一个三角形,从而所求N的最小值为n2+1.
设2n个已知点间连有n2+1条线段,且这些线段不构成任何三角形.设A是2n个点中引出线段条数最多的一个点,共引出k条线段{ABj|j=1,2,…,k}.于是{B1,B2,…,Bk}中任何2个点之间都没有连线,否则必构成三角形.因而,从任一Bj引出的线段条数不超过2n-k.
除了A,B1,B2,…,Bk之外还有2n-k-1个点,其中任何一点引出的线段条数不超过k.于是得到
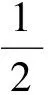
k(2n-k)≤n2,
矛盾.
评注本题用了3种方法求解,都是先通过例子确定出N的一个下界,然后用不同的方法证明这个下界是可以达到的,进而求出N的最小值.解法1用数学归纳法,解法2运用了反证法与柯西不等式,解法3则是运用了极端原理.
例2已知平面上一个含有n个点的集合S,具有如下性质:
(1)S中任意3个点不共线;
(2)对S中每个点P,在S中至少有k个点到点P的距离相等.
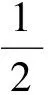

解得


解得

例3300个工作人员分成3个部门,每个部门100人,每2个人或者互相认识,或者互不认识.证明:存在不同部门的2个人,使得在第3个部门中,或有17个人都认识他们,或有17个人都不认识他们.
分析将3个部门的工作人员所成的集合分别记为A,B,C,集合中的元素都称为顶点.在任何2个不属于同一集合的顶点之间都连一条边,2个人认识时边为红色,不认识时为蓝色(这称为双色三部图).共连得1003个三角形.如果三角形中的某个角的2条边同色,就称为同色角.
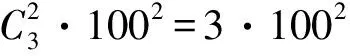
评注化归是指把要解决的问题,通过某种转化,归结到一类已经解决或者能比较容易解决的问题中去,最终获得原问题的一种解题策略.前苏联数学家雅诺夫斯卡娅在回答“解题意味着什么”时说:“解题就是意味着把所要解决的问题转化为已经解决的问题.”
例4设正整数n≥3,而a1,a2,…,an是任意n个互异的实数,其和为正数.若它的一个排列b1,b2,…,bn满足:对任意的k=1,2,…,n,均有b1+b2+…+bk>0,则称这个排列是好的,求好的排列个数的最小值.
分析考察最坏的情形:要使b1+b2+…+bk>0很难满足,只需让负数尽可能多,即取a2,a3,…,an均为负数,a1=-a2-a3-…-an+1.此时对于任何一个好的排列(b1,b2,…,bn),均有b1=a1,而b2,b3,…,bn可以是a2,a3,…,an的任意排列,故此时共有(n-1)!个好的排列.下面证明至少有(n-1)!个好的排列.注意到(n-1)!是将a1,a2,…,an排在圆周上的不同圆排列的个数,因此首先证明每一个圆排列对应一个好排列.为了方便,称好排列的首项为好数,下面只需证明每个圆排列中必存在一个好数.
证法1对n进行归纳.当n=1时,结论显然成立.假设对一切n
证法2利用极端性原理.对任何一个圆排列(b1,b2,…,bn),考察所有以bi为首项的部分和:bi+bi+1+…+bi+t,其中大于n的下标取模n的余数,对所有i=1,2,…,n和所有t=0,1,2,…,n-1,必存在一个最小的部分和bi+bi+1+…+bi+t,因为至少存在一个非正数,所以bi+bi+1+…+bi+t≤0.在所有这样的最小和中又设项数t+1最大的一个为bi+bi+1+…+bi+t,下面证明bi+t+1是好数.
实际上,若存在正整数k,使
bi+t+1+bi+t+2+…+bi+t+k≤0,
则(bi+bi+1+…+bi+t)+(bi+t+1+bi+t+2+…+
bi+t+k)≤bi+bi+1+…+bi+t,
这与bi+bi+1+…+bi+t的和最小且项数最多矛盾.
由于共有(n-1)!个圆排列,而每个圆排列至少对应一个好排列,且不同的圆排列对应的好排列是不同的,故至少有(n-1)!个好排列.综上所述,所求最小值为(n-1)!.

(注:图G的2个不同顶点u,v之间的一条长度为k的路径是指一个顶点序列u=v0,v1,…,vk=v,其中vi与vi+1相邻,i=0,1,…,k-1.)
证明对任意2个不同顶点u,v,若u,v之间的最短路径长度为k,则称它们之间的距离为k.考虑图G,其顶点集为{x1,x2,…,x3n2-n,y1,y2,…,yn},yi与yj相邻(1≤i 易知xi与xj的距离不超过3,图G符合条件,G共有 条边. 下面证明满足题设条件的图G=G(V,E)的边数至少为N.设X⊆V是所有度等于1的顶点的集合,Y⊆(VX)为剩余顶点中与X中某个顶点相邻的所有顶点的集合,Z⊆V(X∪Y)为剩余顶点中与Y中某个顶点相邻的所有顶点的集合,W⊆V(X∪Y∪Z),可得到以下性质: 性质1Y中的任意2个顶点都相邻. 这是因为若y1,y2∈Y是2个不同顶点,设x1,x2∈X分别与y1,y2相邻,由x1与x2的距离不超过3,可知y1与y2相邻. 性质2W中的顶点与每个Y中顶点的距离均为2. 若不然设w0∈W,y0∈Y的距离不小于3(距离显然不小于2),设x0∈X与y0相邻,则w0与x0的距离不小于4,与题设矛盾.性质2成立,由此可知每个W中的点都与某个Z中的点相邻. 当y≤n-1时,由于每个顶点的度不超过4n,故 x+z≤y[4n-(y-1)]=y(4n+1-y)≤ (n-1)(3n+2)=3n2-n-2, w≥3n2-y-y(4n+1-y)≥3. 若a>1,则 N; 评注构造与论证是组合极值的2个方面,构造是构造合乎条件的对象或构造使命题不成立的反例.论证是论证某种量满足某个不等式或论证某些对象具有某种性质,两者都需要灵活的思维、丰富的想象及创造性的构想. 数学竞赛是解题的竞赛,只有通过问题才能学会解题.要提高组合解题能力,必须反复练习,在解各类题中,善于总结,不仅要寻找各种不同的解法,更要找出最佳的方法.我们应当注意数学思想与数学审美,不断提高鉴赏能力.