简谈一道中考试题的教学功能

●

(安宁镇荞窝监狱组织人事科 四川西昌 615014)

简谈一道中考试题的教学功能

●王承宣

(安宁镇荞窝监狱组织人事科 四川西昌 615014)

笔者赏析了四川省的一道中考试题，认为有较强的教学功能，浅析如下，供教研参考.

图1

(1)求点A，B，C的坐标；

(2)如果抛物线y=ax2+bx+c经过点A,B,C，求这条抛物线的解析式；

(3)求第(2)小题中抛物线的对称轴和顶点坐标.

1 强化选择衔接，激发学习兴趣

该题将一个涉及圆的几何图形放入直角坐标系并融入代数知识考查，虽不是独创，但它的高中味很浓，有利于人才的选拔和初高中知识的衔接.按高中学生做的思路解答如下(初中生也能理解)：

⊙Q的方程为

将点A的坐标代入,得

整理得

由题意取x1=1,即|OA|=1,从而|OC|=2,故A(1，0)，B(4，0)，C(0，-2).至此，第(2)小题和第(3)小题也迎刃而解.

对初中生而言，为了避开圆的方程之说，可以换言之：在Rt△AQE中，根据勾股定理得

学生上了高中后便能体会这是将点A的坐标代入圆的方程所得，知识得到了升华，衔接凸显，兴趣激发，选拔功能实现.

2 代数几何有效结合，优化解题过程

求点A，B，C的坐标在该题中起制约作用，一些考生解析几何功底不够好，将圆放入直角坐标系后，由于坐标系“一叶障目”的干扰，不能有效地使用切割线定理：OC2=OA·OB.经实验得知，若去掉坐标系，学生很容易就看出了切割线定理的使用环境.因此，中考复习应强化“在坐标系中处理几何问题”的意识.

该题将代数和几何有效结合是最优解法.

解法2由切割线定理得

OC2=OA·OB,

即

化简得

(以下步骤略.)

与解法1得出圆方程的过程相比，解法2加入了纯几何知识，优化了解题过程.

3 开阔解题视野，培养创新能力

求抛物线解析式，一般是先求出3个点的坐标，再求解析式等.有少部分学生对此提出疑虑,其实该题可以先求解析式，再求点的坐标，从而使学生有创新之感，培养了学生的创新能力.分析如下：

解法3设A(x1,0),B(x2,0),x2>x1>0,则B(x1+3,0).由切割线定理及一元二次方程根与系数的关系得

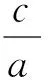
即ac=1.

(1)

由

(x2-x1)2=9,

得

(x2+x1)2-4x1x2=9,

从而

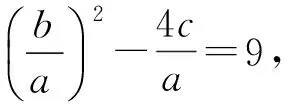
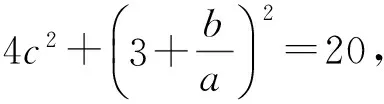
式(3)+式(2)，整理得

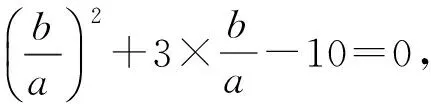
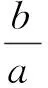
将b=-5a代入式(2)解得

从而

所求解析式为

由x2-x1=3,x1+x2=5,得x1=1，从而得到点A，B，C的坐标(略).

解法3虽谈不上最优，但它起到了开阔解题视野的作用.学生的思维仿佛逛了一趟“数学的桃花源”，通过解题使学生形成通过辛勤耕耘开辟实在的数学桃花源的意识.

其实该题还可以用纯几何知识求出⊙Q的半径R，即由

得

2R2-3R-5=0,

综上所述，该题不仅很好地融合了代数与几何知识，而且解法灵活，教学功能多样，不失为一道好题.