巧补形 妙解题

●

(晋州市实验中学 河北晋州 052260)

巧补形妙解题

●苑建广

(晋州市实验中学 河北晋州 052260)

对于给定“非规则”图形的数学题，通常不易打开思路.这时可综合考虑题设、结论及所给图形的特征，通过“补形”将原图形巧加完善，揭示本质，释放内涵.由于我们对等腰三角形、直角三角形、等边三角形、等腰梯形、矩形、菱形、正方形、圆等特殊图形较为熟悉，因此，若能通过图形变换或做辅助线把非规则图形化归为这些特殊图形，则往往能够化分散为集中，迅速找到解题方法.现归类例析，仅供读者探究之用.

1 补成正三角形

例1如图1，六边形ABCDEF的6个内角都相等．若AB=1，BC=CD=3，DE=2，则这个六边形的周长等于________.

(2011年天津市数学中考试题)

图1 图2

分析由于六边形ABCDEF的每个内角都相等(均为120°)，且每个顶点处的外角均为60°，这样便容易想到将六边形完善成正三角形.分别作边AB，CD，EF所在的直线，并相交于点M，N，P.易判断△MAF，△PDE，△NBC，△MNP均为正三角形，于是

NB=NC=BC=3，PD=PE=DE=2，

得

PN=NC+CD+PD=8.

由△MNP是边长为8的正三角形，得

MA=MN-NB-AB=8-3-1=4，

即

AF=FM=AM=4，

同理

EF=PM-FM-PE=8-4-2=2，

进而可得六边形ABCDEF的周长为15.

例2如图2，已知△ABC为等边三角形，延长BC到D，延长BA到E，并且使AE=BD.联结CE，DE,求证：EC=ED．

(2000年内蒙古自治区数学中考试题)

分析直接通过推导∠ECD=∠EDC来证明EC=ED比较困难.此时可结合题、图及结论特征，将原图补成正三角形：延长BD至点F，使DF=BC，联结EF.因为AE=BD，△ABC为等边三角形，所以

BE=BF，∠B=60°，

从而△BEF为等边三角形，得

∠F=60°，EB=EF.

又易知CB=DF，则

△EBC≌△EDF，

得

EC=ED．

2 补成直角三角形

(2009年内蒙古自治区呼和浩特市数学中考试题)

分析由AB⊥AD，BC⊥CD，知可将原图补成直角三角形：延长DA，CB交于点E，则∠ABE=60°，∠E=30°．在Rt△EAB中，

AB=4，∠E=30°，

得

BE=8，AE=4；

在Rt△DEC中，

CD=5，∠E=30°，

得

CE=15，

于是

因此四边形ABCD的面积为

图3 图4

例4如图4，在梯形ABCD中，AD∥BC，∠B+∠C=90°，AD=1，BC=3，E，F分别是AD，BC的中点，则EF=________.

(2004年江苏省宿迁市数学中考试题)

分析由∠B，∠C互余，知可考虑将原图补成直角三角形.延长BA，CD，相交于点P，联结PF.设PF与AD交于点E′，由AD∥BC，得

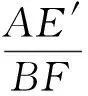
又由BF=FC，得AE′=DE′，即点E与点E′重合.在Rt△PBC中，有

在Rt△PAD中，有

于是

EF=PF-PE=1.

3 补成等腰三角形

例5如图5，在梯形ABCD中，AD∥BC，CE是∠BCD的平分线，且CE⊥AB，E为垂足，BE=2AE.若四边形AECD的面积为1，则梯形ABCD的面积为________.

(2011年内蒙古自治区呼和浩特市数学中考试题)

分析由已知条件“CE平分∠BCD”和“CE⊥AB”，结合等腰三角形“三线合一”，可想到延长BA，CD相交于点F.易知△CBF为等腰三角形(CB=CF)，且BE=EF,故△CBE≌△CFE.设AE=a，则BE=EF=2a，AF=a.

另设△CBE的面积为S，则△FAD的面积为S-1，△CBF的面积为2S.由△FAD∽△FBC，得

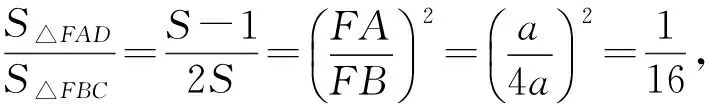
图5 图6

例6如图6，在等腰梯形ABCD中，AD∥BC，∠C=60°，AD=10，AB=18，求BC的长．

(2005年海南省数学中考试题)

分析分别延长BA，CD交于点E．由

AD∥BC，AB=CD，得

∠B=∠C=60°，∠EAD=∠EDA=60°，

从而△EBC与△EAD均为等边三角形，得

BC=BE=AB+AE=AB+AD=18+10=28．

4 补成正方形

例7如图7，在△ABC中，∠BAC=45°,AD⊥BC于点D，已知BD=6,CD=4,则高AD的长为________．

(2008年湖北省鄂州市数学中考试题)

分析由∠BAC=45°，可联想到完善图形:作△ABD关于AB对称的△ABM，再作△ACD关于AC对称的△CAN.延长MB，NC交于点P，易知四边形AMPN是正方形.若设AD=x，则正方形的边长等于x，BP=MP-MB=x-6，CP=NP-NC=x-4.在Rt△BCP中，有

(x-6)2+(x-4)2=(6+4)2，

解得x=12，即高AD=12.

图7 图8

5 补成矩形

例8同例1.

分析如图8，过点B作AF的垂线，分别交AF，CD所在的直线于点M，N；再过点E作AF的垂线，分别交AF，CD所在的直线于点P，Q.易知四边形MNQP为矩形.

在Rt△MAB中，AB=1，∠MAB=60°，可得

同理，在Rt△NBC中，可得

在Rt△QDE中，可得

因此

MP=NQ=NC+CD+QD=

又

得

在Rt△PEF中，由∠PEF=60°，得

EF=2，PF=1,

从而

因此六边形ABCDEF周长为15.

6 补成菱形

例9如图9,在凸五边形ABCDE中，∠A=∠B=120°，EA=AB=BC=2，CD=DE=4，则它的面积为________.

(第44届美国AHSME试题)

分析结合题、图特征，容易想到补全原图形为菱形：延长EA，CB交于点F.易知△FAB为正三角形，边长为2,四边形FCDE为菱形，边长为4.于是

图9 图10

7 补成平行四边形

例10同例1.

分析如图10，延长FA，CB交于点M，延长FE，CD交于点N.易知△MAB，△NDE均为正三角形，且四边形MCNF为平行四边形.从而

MB=MA=AB=1，EN=ND=ED=2，

于是

MC=MB+BC=1+3=4.

因为四边形MCNF是平行四边形，所以

FN=MC=4，

得

EF=FN-EN=4-2=2.

同理可得AF=4，则六边形ABCDEF的周长为15.

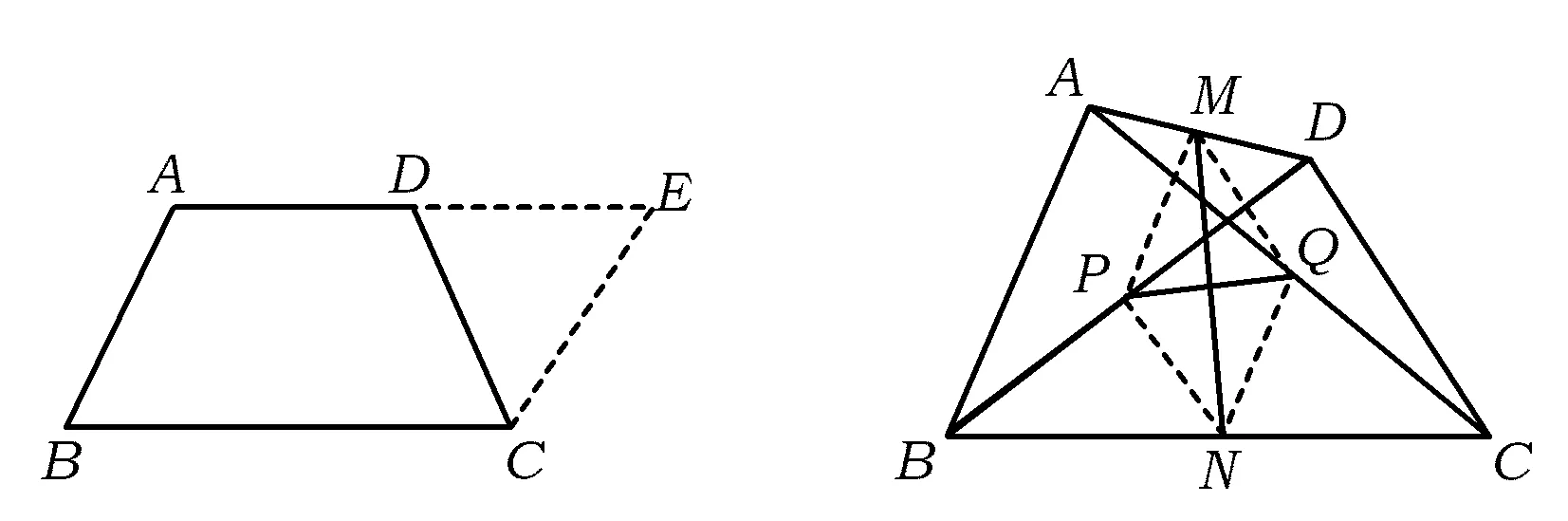
图11 图12

例11同例6.

分析如图11，过点C作CE∥BA交AD的延长线于点E．易知四边形ABCE是平行四边形，△DEC是等边三角形，则

DE=DC=AB=18，

从而

BC=AE=AD+DE=10+18=28．

例12如图12，在四边形ABCD中，AB=CD，M，N，P，Q分别是AD，BC，BD，AC的中点．求证：MN与PQ互相垂直平分．

(2007年湖南省株洲市数学中考试题)

分析欲证MN与PQ互相垂直平分，则四边形MPNQ必为菱形.联结MP，PN，NQ，QM，补全成菱形,由

AM=MD，BP=PD，

得

从而

PM=NQ，且PM∥NQ，

即四边形MPNQ是平行四边形.又由AB=DC，可得

PM=MQ，

从而平行四边形MPNQ是菱形,MN与PQ互相垂直平分．

8 补成等腰梯形

例13同例1.

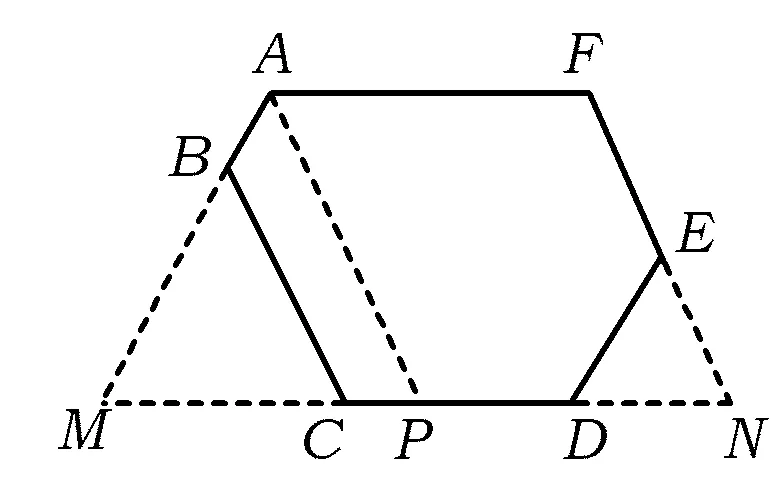
图13

分析如图13，延长AB，DC交于点M，延长FE，CD交于点N，过点A作AP∥FN交MN于点P.易知四边形AMNF为等腰梯形，△MBC，△MAP，△NDE是正三角形，四边形APNF为平行四边形，且AM=FN=4，MN=8,于是

MP=AM=4，

PN=MN-MP=8-4=4，

从而

AF=PN=4.

又EN=DE=2，得

EF=FN-EN=4-2=2，

因此原六边形周长为15.

9 补成圆

圆有着许多美妙的性质.不少数学难题,通过构造“辅助圆”往往能出奇制胜.

例14如图14，在四边形ABCD中，AB=AC=AD.若∠CAD=76°，则∠CBD=________.

(2008年山东省济宁市数学中考试题)

图14 图15

例15如图15，若PA=PB，∠APB=2∠ACB，AC与PB交于点D，且PB=4，PD=3，则AD·CD

等于________.

(2001年TI杯全国初中数学竞赛题)

分析看到“PA=PB”和“∠APB=2∠ACB”，容易想到：以点P为圆心、PA长为半径作圆.此时，点C必然落在⊙P上.作直径BT，联结AT,则BT=8，TD=7，BD=1.易证△BCD∽△ATD,则

即

AD·CD=TD·BD=7.

由此可见，巧妙“补形”，能把条件化分散为集中，便于整体思考和运用，可以迅速释放题、图内涵，打开解题思路.这一点提示我们，遇到平面几何问题时，要善于借助各种手段把不规则、不标准、不熟悉的图形向规则、标准、熟悉的图形转化，从而沟通条件和结论之间的联系，化生为熟，化难为易.