巧拼三角板求tan15°的值

●

(襄州区黄集镇初级中学 湖北襄阳 441123)

巧拼三角板求tan15°的值

●赵国瑞

(襄州区黄集镇初级中学 湖北襄阳 441123)

图1 图2

或许一些学生会认为，三角板的作用只是用来作图，其实不然，它里面包含的数学知识可多啦！利用三角板求15°角的三角函数值便是它的一个巧妙应用，下面仅以求tan15°的值为例．

1 利用15°=45°-30°

方法1将一副三角板按图3所示的方式拼接，其中AC与AE在一条直线上，BC与AD交于点M，则∠BAD=45°-30°=15°．过点M作MN⊥AE于点N，则△MNC是等腰直角三角形，△AMN是半等边三角形．

图3 图4

得

故

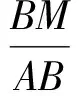
方法2将一副三角板按图4所示的方式拼接，其中AB与AD在一条直线上，BC与AE交于点M，则∠CAE=45°-30°=15°．过点M作MN⊥AE于点N，则△MNC是等腰直角三角形，△ABM是半等边三角形．

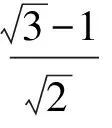
得

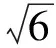
故

评注将方法1中的△ADE绕点A逆时针旋转15°即是方法2的拼接方式．

方法3将一副三角板按图5所示的方式拼接，其中等腰直角三角形的斜边与半等边三角形的较长直角边重合，BD与AE交于点M，则∠BAE=45°-30°=15°．

以下解法同方法1．

评注将方法1中的△ADE绕点A顺时针旋转30°再沿直线AC翻折即是方法3的拼接方式．

图5 图6

方法4将一副三角板按图6所示的方式拼接，其中AB与AE在一条直线上，BC与AD交于点M，则∠CAD=45°-30°=15°．

以下解法同方法2．

评注将方法3中的△ADE绕点A逆时针旋转15°即是方法4的拼接方式．

2 利用15°=60°-45°

方法5将一副三角板按图7所示的方式拼接，其中AC与AE在一条直线上，AB与DE交于点M，则∠BAD=60°-45°=15°．过点M作MN⊥AE于点N，则△AMN是等腰直角三角形，△MNE是半等边三角形．

得

故

图7 图8

方法6将一副三角板按图8所示的方式拼接，其中AD与AB在一条直线上，AC与DE交于点M，则∠CAE=60°-45°=15°．过点M作MN⊥AE于点N，则△ADM是等腰直角三角形，△MNE是半等边三角形．

得

故

评注将方法5中的△ABC绕点A逆时针旋转15°即是方法6的拼接方式．

图9 图10

方法7将一副三角板按图9所示的方式拼接，其中AB与AE在一条直线上，AC与DE交于点M，则∠DAC=60°-45°=15°．

以下解法同方法5．

评注将方法5中的△ABC绕点A顺时针旋转45°再沿直线AE翻折即是方法7的拼接方式．

方法8将一副三角板按图10所示的方式拼接，其中AC与AD在一条直线上，则∠BAE=60°-45°=15°．过点B作BM⊥AE于点M，BF⊥AC于点F，BF的反向延长线交AE于点N，则△ABF是等腰直角三角形，△BNM是半等边三角形．

以下解法同方法6．

评注将方法7中的△ABC绕点A逆时针旋转15°即是方法8的拼接方式．

3 利用15°=90°-45°-30°

图11

方法9将一副三角板按图11所示的方式拼接，其中等腰直角三角形的斜边与半等边三角形的较长直角边重合．过点D作DE∥AC交BC的反向延长线于点E,过点A作AF∥BC交DE的反向延长线于点F,则∠DAF=90°-45°-30°=15°，△BDE是等腰直角三角形．

故

上面的拼接方式中，2个三角板都有一条边(或其中的一部分)重合．其实，我们也可以无需使一条边(或其中的一部分)重合，但要保持其中一条边平行，同样可以求出tan15°的值．如图12(其中EF∥BC)和图13(其中AC∥DF)，你能根据这2个图形求出tan15°的值吗？

图12 图13

[1] 郭红茹，郑泉水.巧拼三角板求sin15°的值[J].中学生数学,2011(9)：15.