基于感性认识下的理性课堂——对“分式”复习课的思考

●

(南京师范大学附属中学新城初级中学 江苏南京 210019)

基于感性认识下的理性课堂——对“分式”复习课的思考

●陆军

(南京师范大学附属中学新城初级中学 江苏南京 210019)

1 背景分析

1．1 课题的由来

本节课是“分式”的复习课．笔者从教和学2个角度，对传统复习课的模式进行改进，让学生经历一个从感性认识上升到理性认识的过程，帮助学生建构知识的体系，促进学生对数学本质的理解．

1.2 学情分析

(1)本节课的学习者是8年级的学生，笔者教学班级的学生有较强的独立思考能力和一定的数学交流意识；

(2)学生经过“不等式、分式”的学习，已具备从具体的数向抽象的字母、代数式转化的能力和数学经验．

1.3 教学目标

(1)对本章知识进行梳理，使所学知识系统化和条理化；

(2)进一步丰富对分式概念的认识，并能有条理地阐明自己的观点；

(3)能解释一些简单代数式的实际背景或几何意义．

2 情境再现

2.1 问题情境

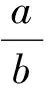
问题的开放性，给学生提供了个性化展示的机会，在解决问题的过程中，感受分式数学模型在生活中的广泛应用．

2．2 感性认识

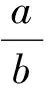
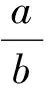
学生已具备的生活经验和感性认识，使学生体会分式是刻画现实世界有效的数学模型成为可能．

师：很好！同学们能用数学的观点解释吗？

2.3 理性分析

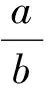
学生独立思考，在有了想法后，进行相互讨论．

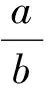
学生在小学阶段中已经有了知识经验：2个分数，分子一样，在分母和分子是正数的条件下，分母小的反而大．

师：谈一谈你做该题的感受．

生：比较2个分式的大小，可以用做差法，通过通分，结果与0比较大小．

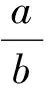
师：根据我们的生活经验，请同学们猜想一下糖水变甜了还是变淡了？

生：与加进去的糖水的浓度有关．

师：与所加糖水的浓度有怎样的关系？

师：怎样用数学符号来说明结论的正确性？大家讨论一下．

课堂一下就变得热闹起来，在讨论后主要有2种方法，教师请2位学生阐述自己的观点．

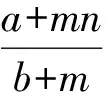
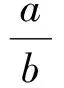
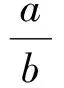
2.4 感性和理性之间的相互转化

师：其实数学中还有很多问题，可以借助这个模型进行解决．

生(齐声)：n杯糖水浓度一样，把它们混合在一起后的糖水浓度不变．

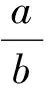
师：我们所研究的不等式的2边都是比值形式，而面积更多的是线段的乘积关系，如何转化？

在教师的点拨下，学生陆续得到结论．

图1

3 教学反思

法国哲学家柏格森认为：人类认识事物有两种根本不同的方法，一种是围着对象转，被称为理性；另一种是进入事物内部，被称为感性．按皮亚杰的儿童认知发展理论的描述，8年级的学生，多处于具体运演阶段和形式运演阶段的转换期，他们能区分内容的真实和形式的假设，但整体水平还不是很高．因此，在教学中不仅要考虑到数学学科的特点，更应遵循学生的学习规律，强调从学生的生活经验和感性认知出发，从具体问题到抽象概念，让学生经历一个数学建模的过程，鼓励学生在观察、分析的基础上，对数学对结论进行归纳、猜测、论证．

3.1 从生活的感性情境中引发学生理性的逻辑思考

数学学科具有较强的抽象性，而抽象的数学知识往往具有深刻的生活背景，我们可以让数学教学更贴近生活．本节课从解释分式所表示的实际意义入手，让学生积累感性经验，为后继的数学理解提供知识保障，感性的情境是学生理性思考的载体．

3.2 从解题的感性经验中提升学生理性的归纳能力

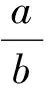
心理学认为感性认识是学生理解知识的基础，直观是数学抽象思维的途径和信息来源．因此，课堂应该是感性认识下的理性课堂．