基于SPH方法的浅水爆炸研究

刘翠丹，明付仁，丛 刚，王 超

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

0 引言

爆炸冲击波攻击舰船和潜艇属于水下爆炸在国防上的应用，水下爆炸产生的高压冲击波会使舰船发生毁灭性破坏。浅水爆炸由于边界效应，冲击波压力十分复杂，对浅水环境中的舰船打击作用显著加强，因此研究浅水爆炸中冲击波的特性对舰船受攻击时的冲击响应预报及舰船防护结构设计具有重要意义。

对于沉底和自由面爆炸，已经有不少探索，但是对于浅水爆炸来说，目前可参考的资料还较少，这是由于浅水爆炸要考虑水底及水面双重的影响，情况较复杂。在试验方面，刘文华［1］等通过单个球形装药浅水爆炸研究了几种参数对水中冲击波峰值压力的影响，探索了边界条件影响下冲击波的变化规律;高永军［2］等对浅层水中爆炸冲击波参数和空间流场的压力分布进行分析，得出试验范围内的冲击波压力的经验公式;张鹏翔［3］等分析浅水爆炸的水面切断现象对冲击波的正压作用时间和比冲量的影响，对实验数值进行回归，得到精度较高的回归公式。在数值模拟方面，顾文彬［4］等数值模拟研究水底和水面效应对冲击波的影响;孙百连［5］等对沉底2个装药爆炸进行数值模拟，将其与单个装药爆炸和无限水域2个装药同时爆炸进行了对比，研究水底水面对冲击波的影响。在理论方面，张鹏翔［6］等探讨了浅水爆炸中的冲击波切断现象，主要分析了切断现象的特性，产生机理以及对冲击波的影响，对两类切断现象进行了探讨。上述文献中大多数采用试验的方法进行分析，还有少数采用有限元分析。而传统有限元方法分析爆炸问题存在弊端，特别是大变形、运动交界面问题，经常导致计算崩溃甚至无法计算。近年来引起关注的是新一代计算方法——无 网 格 法。 SPH (Smoothed Particle Hydrodynamics)方法作为一种拉格朗日形式的无网格粒子法具有自适应、无网格、粒子形式等特性，在大变形的流体动力学问题上具有独特优势，适合于解决水下爆炸产生的大变形问题。

本文通过SPH方法进行数值模拟，再现了浅水爆炸中的基本过程，分析冲击波的压力峰值和冲量特性、研究爆深和泥沙密度等参数对浅水爆炸的影响，旨在揭示近边界爆炸冲击波传播特征，为舰船水下爆炸的载荷确定、结构响应预报及防护结构设计提供参考。文中使用的程序对自由场中的水下爆炸模拟，并将结果与经验公式对比，验证了程序的精度，限于篇幅，这里不予呈现。

1 基本理论

1.1 SPH控制方程

拉格朗日描述下的流体控制方程可写作一系列偏微分方程，也就是著名的Navier-Stokes方程，其中包括质量守恒方程、动量守恒方程和能量守恒方程。SPH方法是应用核近似和粒子近似对N-S方程进行离散，得到以下SPH形式的控制方程［7］:

以上分别为连续性方程、动量守恒方程、能量守恒方程。Π采用Monaghan型人工粘度项［8］，下标i，j表示相互作用的1对粒子，上标α，β表示沿坐标轴的方向。

1.2 状态方程

1.2.1 TNT状态方程

TNT爆炸产生的爆轰产物采用Jones-Wilkins-Lee状态方程［9］:

式中:η为爆轰产物密度与初始炸药密度的比值，即η=ρ/ρ0;A，B，R1，R2和ω为与炸药状态有关的常数。

1.2.2 水的状态方程

水在爆炸冲击波传播阶段采用Mie-Grüneisen状态方程［10］，其具体形式取决于水的状态。

在压缩状态下水的压力为

在膨胀状态下水的压力为

式中:μ为压缩比;e为单位质量内能;μ=η-1，当μ＞0时，水处于压缩状态，当μ＜0时，水处于膨胀状态;C0为声速;γ0为 Grüneisen系数;a为体积修正系数;S1;S2;S3为试验拟合系数。

1.2.3 泥沙的状态方程

泥沙的状态方程引用文献 ［11］中的经验形式。

多项式状态方程是流体物态方程的经验形式，常用其拟合Mie-Grüneisen物态方程。多项式状态方程由下式给出

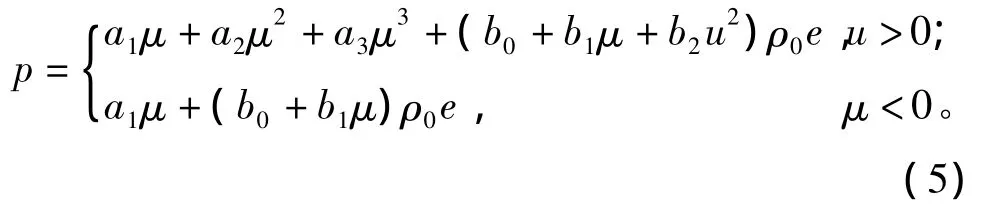
式中:a1，a2，a3，b0，b1，b2为物态方程经验系数;μ，e与前同。而Grüneisen系数表示为

1.3 浅水爆炸的基本理论

同时受水面水底影响的装药水中爆炸定义为浅层水中爆炸［12］。浅水爆炸冲击波主要受水面、水底2种界面的影响，是一个涉及水、目标运动及边界效应的复杂爆炸动力学问题。

稀疏波，该波经过一段时间后到达测点，使测点处的压力受到削弱，冲击波在水底反射，当反射冲击波遇上入射波，会使得测点处的压力峰值比无限场中大。水面反射波到达测点，与入射冲击波或反射冲击波作用，使得合成压力低于水介质的静压力，表现在压力曲线上波形被削去一截，称作水面切断现象［3］。

水底对爆炸效果的影响是多方面的。爆炸冲击波到达水底后，产生反射冲击波在水中传播，同时产生纵波和横波。当这2种弹性波与水底的分界面作用时产生瑞利波。瑞利波在水底的不规则反射形成前驱波，使压力增加10%～20%。反射波追上入射波，二者融合形成马赫波。与无限水域相比马赫波使压力增加3%～7%，可见水底对冲击波的影响不可小视［12］。随着测点高度或测点距爆心距离增加，水底影响减小［4］。装药量和水底材料一定时，爆深不同，测点压力有很大不同。测点相同，随着爆深的增加，相同比例距离上的峰值压力增加［13］。

2 浅水爆炸数值模拟

2.1 数值模型

本文采用SPH方法模拟浅水爆炸，利用Fortran编程建模，模型图见图1。

图1 浅水爆炸模型Fig.1 Shallow water explosion model

图中上面为水域，下面为泥沙水底，正方形TNT炸药位于水域的中央。模型中常量主要有:水深a=0.600 m，水底泥沙尺寸b=1.500 m，c=3.000 m，装药 TNT质量 m=0.360 kg，直径 d=0.045 m。模型中的变量有炸药中心距自由面距离高度h、测点距爆心的水平距离e和垂向距离f以及泥沙的密度ρ。浅水爆炸模型中变量h=0.300 m，ρ=1 800 kg/m3。为了研究浅水爆炸时自由面和泥沙水底的影响，本文将其计算结果和相同药量无限水域爆炸的计算结果进行对比。无限水域爆炸模型长3.0 m，宽2.1 m，炸药位于水域中心，TNT尺寸与浅水爆炸计算模型相同。

2.2 基本物理现象

炸药水中爆炸时，在装药和介质的界面处，爆炸产物以极高的速度向周围扩展，强烈地挤压周围的水介质，使其压力、密度、温度突然升高，形成初始冲击波。

当水域比较浅时，底部效应与自由面效应都不能忽略，自由面效应和底部效应共同对直达波产生作用。图2显示了不同时刻下浅水爆炸计算模型的压力云图和粒子分布图，从图中可知，TNT引爆后，会产生压力极高的强冲击波在水域中传播，在70 μs时是冲击波到达边界之前的云图，此时冲击波还没有受到边界的影响;在130 μs时，冲击波传播至自由面处，反射一列稀疏波，使稀疏波的影响区域压力降低，由于自由面附近爆炸会削弱气泡对舷侧的攻击效果［14］，因此可以得出结论，若武器在浅水中靠近自由面爆炸时，会削弱爆炸产物的攻击效果。此时冲击波传到水底在泥沙中产生圆形的冲击波向外传播，泥沙中的冲击波压力高于水中的冲击波压力。至200 μs时，2种反射波相向传播，即将相遇;至380 μs时，2种反射波相遇，稀疏波的影响范围逐渐增大，涵盖近自由面的大部分区域，此时，水下爆炸冲击波的高压高能作用使自由面发生了水冢现象。在水和泥沙的交界面处，由于自由面反射的稀疏波致使泥沙中冲击波压力迅速降低，逐渐和水中压力相同。同时冲击波在水底的反射冲击波遇上入射波，在近水底处产生前驱波，此波与入射波叠加，使测点处压力变大。至540 μs时，水冢不断地增大，由于爆炸冲击的作用，邻近自由面的水粒子产生凸起的现象，随着爆炸产生的气体接近底部泥沙，气体的非球形就逐渐变得明显，这里的现象与文献 ［14］中的结论一致，即随着气泡距离壁面越近，气泡非球状出现的越早［14］。

图2 浅水爆炸粒子分布图及压力云图Fig.2 Particle distribution and explosion pressure pictures of shallow water explosion

2.3 压力及冲量特性

图3显示了e=0.40 m，f=0.25 m，f=0.01 m，f=-0.24 m时，浅水爆炸和无限水域爆炸的压力时程对比曲线。

图3 不同测点的压力时程曲线Fig.3 Pressure process curve of different point

当f=0.25 m时，由于测点位置靠近自由面，此时冲击波压力主要受自由面影响，受底部影响较小，自由面使冲击波产生“切断”效应，即把冲击波的波尾截掉，减小冲击波的冲量和能量，并使这部分能量转化为流体向上运动的动能。

当f=-0.24 m时，由于测点位置靠近水底，此时冲击波压力主要受底部影响，从0.2 ms开始，水底反射波传到测点，浅水爆炸压力值大于无限水域压力值。这是由于泥沙的反射作用使冲击波变强。到0.45 ms，自由面反射波到达测点，使得压力值降低，小于无限水域的压力值。

当f=0.01 m时，测点位于爆心的水平左侧，受到自由面反射波和水底反射波的双重作用，压力曲线既出现了“截断”效应，又出现了压力峰值交错。

冲击波冲量是丈量冲击波强弱的标志，表1中给出了2种工况下的测点冲量。

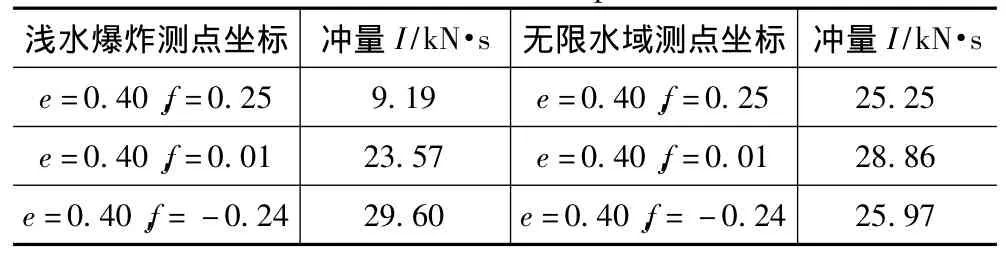
表1 测点冲量Tab.1 Point impulse

自由面会使冲击波的冲量减少，而底部会使冲击波的冲量增大，分析上表可知，当f=0.25 m时，测点以自由面影响为主，冲量减少了36%;当f=-0.24 m时，测点以底部影响为主，冲量增加了14%;当f=0.01 m时，测点同时受到自由面和底部的影响，作用效果存在一定的抵消。

2.4 不同爆深的影响

不同爆深对浅水爆炸的压力峰值有影响，为了研究该问题，本文分别取爆深h=0.1 m，h=0.3 m，h=0.5 m，其余的参量都与浅水爆炸模型相同。经过程序计算，得到对比云图 (图4)和压力时程曲线(图5)。

从图4可以看出，h越大，浅水爆炸产生的水冢现象就越不明显，若爆深足够大，则不会出现水冢现象。

图5显示了3种爆深的压力时程曲线。这里由于爆深差别较大，3个测点集中选择在爆心的左侧附近。

对于不同爆深下相对位置相同的测点，当h=0.1 m时，爆心靠近水面，压力曲线主要受到近水面反射波的影响，出现明显的截断，压力峰值也迅速下降，压力曲线尾部出现截断效应。当h=0.5 m时，爆心接近水底，压力曲线主要受底部影响，脉宽变大，作用时间变长。而h=0.3 m时，测点同时受到自由面和底部的影响，压力曲线先是受水面影响出现截断现象，然后受底部影响延长了作用时间，并且在尾部出现压力波动的现象。

对于同一爆距下的3条曲线，当f=-0.09 m时曲线波动的幅度较其他2条明显。这是由于此时测点距水底较近，流场区域内受底部泥沙影响较大。但是压力峰值比前二者中爆炸的峰值小。这是由于泥沙土壤在高压爆炸产物的作用下，迅速变形成坑，消耗了一部分爆炸能量，引起水底附近冲击波压力的削弱，所以此时水底附近的压力要比前二者小。

冲击波的冲量是压力曲线与坐标轴围成的面积，分析图5可以看出，随着h的降低，冲击波的冲量减少，表2给出了各工况下的冲量值，从数值上也说明了这点。自由面会使冲击波的冲量减少，而底部会使冲击波的冲量增大。分析表2可知，当h=0.1 m时，测点以自由面影响为主，冲量较小;当h=0.5 m时，测点以底部影响为主，冲量较大;当h=0.3 m时，测点同时受到自由面和底部的影响，作用效果存在不同程度的抵消。总结上述分析可知，随着h的增加，冲量会增加。

表2 测点冲量Tab.2 Point impulse

2.5 不同底部泥沙密度的影响

在浅水爆炸中，水底泥沙的密度也是影响压力的因素，通常泥沙的密度范围是1 500～2 700 kg/m3。为了研究该问题，本文分别选取变量泥沙密度为1 500 kg/m3，1 800 kg/m3和2 400 kg/m3这3 种工况，经过编程计算，得到对比云图(图6)和压力时程曲线(图7)。

从图6可以看出，泥沙密度对压力值的影响，随着泥沙密度的增大，压力峰值也相应的增大，增幅约为1.1倍。图6的现象是由爆轰气体(入射波)、水面对冲击波的反射波以及水底对冲击波的反射波三者相互作用形成的，观察图6可知，随着泥沙密度的增大，使得3种波相互作用的现象更加明显，当ρ=2 400 kg/m3时，药包下方的压力明显减小了，与水接近，这是由于泥沙密度增大使水底反射波的压力变大，其与爆轰产生的气体波作用时相互抵消的结果。

图7中分别给出了3个测点的压力时程曲线。

改变泥沙密度主要影响的是水底反射波的特性，从而影响整个冲击波。

当f=0.2 m时，由于测点处于近水面，离水底较远，几乎不受水底反射波的影响，只有爆轰气体和近水面反射波作用，因此3条曲线轮廓几乎重合。而且可以看出，受近水面反射波的影响，压力曲线出现截断现象。

当f=0 m时，从180 μs开始，爆轰气体传到测点，开始产生压力，此时测点位于水域中间，同时受水面和水底的影响。到340 μs，3种波同时到达测点，曲线从此时开始出现不同的现象。设p1500，p1800，p2400为某一时刻的压力值，从图7中可以看出，当t＞340 μs时，p2400＞p1800＞p1500，水底反射波使压力值变大，随着水底泥沙密度的增大，压力增大的比例也相应变大。

当f=-0.2 m时，从200 μs开始，爆轰气体传到测点，开始产生压力，此时测点靠近水底，以底部影响为主，脉宽变大。到260 μs时，水底反射波和爆轰气体同时到达测点，曲线开始出现不同的现象。从图中可以看出，受水底反射波影响，当 260 μs＜ t＜520 μs时，p2400＞p1800＞p1500，随着水底泥沙密度的增大，压力值增大。到520 μs时，水面反射波到达测点，测点此时受3种波作用，从压力曲线可以看出，测点的压力受到削弱。与无限水域相比，无论密度多大，受浅水效应的影响，到540 μs时压力都等于0。

3 结语

浅水爆炸问题目前主要集中在试验研究，而本文针对此类问题采用无网格SPH方法对其进行数值模拟，从不同爆深、不同底部泥沙密度等几个方面进行了研究和思考，得出如下结论:

1)浅水爆炸中截断与增强效应共存，这是由于水面和底部泥沙共同作用的结果。一方面水面效应能够反射稀疏波，减小冲击波的冲量和能量，并使这部分能量转化为流体向上运动的动能，产生截断效应和水冢现象;另一方面，爆炸冲击波与水底冲击作用，到达底部发生反射，使水底快速变形，压实，由此产生的底部效应能够增大冲击波的冲量和能量，使压力作用时间增长，表现为增强效应。

2)不同爆深时，浅水中压力和冲量受水底和水面影响程度不同。当爆深较小时，受水面影响较大，压力曲线出现截断的效应。当爆深较大时，压力曲线主要受底部影响，作用脉宽变大，峰值增大。在爆深从小逐渐增大的过程中，受水面和水底效应共同影响，冲量增大，压力曲线分别经历峰值和脉宽的削弱、峰值和脉宽增大的过程，并且在尾部出现压力波动的现象。随着爆深的增加，水冢现象逐渐变得不明显直至消失。

3)不同底部泥沙密度时，浅水中压力与冲量呈增强趋势。随着泥沙密度的增加，压力峰值增大，3种泥沙密度在380 μs增幅约为1.1倍。随着泥沙密度的增大，底部反射波的增强效应逐渐大于水面反射波的截断效应，3种波(入射波、水面反射波以及水底反射波)相互作用的现象更加明显。

［1］刘文华，罗松林，顾文彬，等.单个球形装药浅层水中爆炸冲击波特性的研究［J］.工程爆破，1999，5(3):1-5.LIU Wen-hua.LUO Song-lin.GU Wen-bin，et al.Research on specific properties of shock wave from explosion of single spherical charge in shallow water［J］.Engineering Blasting，1999，5(3):1-5.

［2］高勇军，陈小波，等.单个球形装药浅层水中爆炸的试验研究［J］.工程兵工程学院学报，1998，14(1):96-100.GAO Yong-jun.CHEN Xiao-bo，et al.Experimentation and research on a spherical-charge explosion under shallow water［J］.Journal of Nanjing Engineering Institute，1998，14(1):96-100.

［3］张鹏翔，顾文彬，等.浅层水中爆炸水面切断现象的实验研究［A］.第七届爆破学术会议论文集［C］.成都:2001:353-357.ZHANG Peng-xiang.GU Wen-bin，et al.Experimental researchesofcutoffphenomenon by watersurface subjected to shock waves generated by explosion in shallowlayer water［A］.The 7th blasting academic conference proceedings［C］.Chengdu:2001:353-357.

［4］顾文彬，孙百连，等.浅层水中沉底爆炸冲击波相互作用数值模拟［J］.解放军理工大学学报，2003，4(6):64-68.GU Wen-bin.SUN Bai-lian，et al.Numerical simulation of explosive shock wave interaction in shallow-layer water［J］.Journal of PLA University of Science and Technology，2003，4(6):64-68.

［5］孙百连，顾文彬，等.浅层水中沉底的两个装药爆炸的数值模拟研究［J］.爆炸与冲击，2003，23(5):460-465.SUN Bai-lian.GU Wen-bin，et al.Numerical simulation of explosion shock wave interaction in shallow-layer water［J］.Explosion and Shock Waves，2003，23(5):460-465.

［6］张鹏翔，顾文彬，等.浅层水中爆炸冲击波切断现象浅探［J］.爆炸与冲击，2002，22(3):221-228.ZHANG Peng-xiang.GU Wen-bin，et al.Discussions of blasting shock waves cutoff in shallow-layer water［J］.Explosion and Shock Waves，2002，22(3):221-228.

［7］LIU G R，LIU M B.光滑粒子流体动力学——一种无网格粒子法［M］韩旭，杨刚，强洪夫，译.长沙:湖南大学出版社，2005.1-432.LIU G R，LIU M B.Smoothed particle hydrodynamics:A mesh free particle method［M］.Changsha:Hunan University Press，2005.1-432.

［8］MONAGHAN JJ，On the problem of penetration in particle methods［J］.Journal of Computational physics，1989，82:1-15.

［9］DOBRATZ B M.LLNL Explosive Handbook［R］.UCRL-52997，Lawrence Livermore National Laboratory，Livermore，CA.1981.

［10］STEINBERG D J.Spherical explosions and the equation of state of water［R］.UCID-20974，Lawrence Livermore National Laboratory，Livermore，CA.1987.

［11］汤文辉，张若棋.物态方程理论及计算概论(第二版)［M］.北京:高等教育出版社，2008.278-300.TANG Wen-hui.ZHANG Ruo-qi.Overview of theory and calculation of the forms equation.［M］.Beijing:Higher Education Press，2008.278-300.

［12］顾文彬.叶序双，等.浅层水中爆炸水底影响的试验研究［J］. 解放军理工大学学报，2001，2(2):55-58.GU Wen-bin.YE Xu-shuang，et al.Experimental studies of bottom influence in shallow-layer water explosion［J］.Journal of PLA University of Science and Technology，2001，2(2):55-58.

［13］顾文彬.叶序双，等.界面对浅层水中爆炸冲击波峰值压力影响的研究［J］.解放军理工大学学报，2001，2(5):61-63.GU Wen-bin.YE Xu-shuang，etal.Peak pressure investigation of exploding wave influenced by interfaces in shallow-layer water［J］.Journal of PLA University of Science and Technology.2001，2(5):61-63.

［14］张阿漫，王诗平，等.不同冲击环境下气泡脉动特性实验研究［J］.力学学报，2011，43(1):71-83.ZHANG A-man，WANG Shi-ping，et al.Experimental study on bubble pulse features under different circumstances［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43(1):71-83.