基于双基地模型的鱼雷自噪声仿真预报
2012-10-20徐园园王明洲蒋继军
徐园园,王明洲,蒋继军,李 斌
(1.中国船舶重工集团公司第七〇五研究所,陕西西安710075;2.水下信息与控制重点实验室,陕西西安710075)
0 引言
鱼雷自噪声直接影响信噪比和信号处理的性能。因此,自噪声的研究与预报对鱼雷的声自导作用距离和探测精度等有着重要意义。
鱼雷在水下航行时,螺旋桨产生的空化或机械振动转化为水下声波传到鱼雷头部声呐,是鱼雷自噪声的重要组成部分。在航速超过20 kn的情况下,自噪声中螺旋桨噪声占主导地位[1]。鱼雷速度越高,螺旋桨噪声越大,相应自噪声也越强。
螺旋桨噪声通过海水传到鱼雷头部声呐的路径如图1所示。通过路径A海洋中的散射体反向散射螺旋桨噪声,引起了体积散射自噪声;通过路径B海面反向散射螺旋桨噪声,引起了海面散射自噪声;路径C为海底散射路径。
本文研究在高频段、高航速条件下,螺旋桨噪声通过A,B,C三种声散射路径传播到鱼雷头部声呐形成自噪声的强度。
1 鱼雷自噪声散射模型
本文依据文献[2-3],区别以往文献资料[4-8]对流噪声和机械噪声的研究,基于双基地的混响散射模型基本理论,推导螺旋桨散射自噪声。但在混响散射模型中杂波噪声为窄带脉冲,时间域上只在脉宽T内有信号,而自噪声在时间域上连续,任意时刻都存在噪声信号,这直接导致了散射体元选法的差异,将在下文中详细叙述。视鱼雷头部声呐为无指向性换能器,设换能器与螺旋桨噪声源的距离(雷长)为L。
1.1 体积散射自噪声
海洋本身或其体积之中包含大量不均匀的粒子,阻挡了照射到它们上的一部分声能,并把这部分声能再辐射回去,将这些散射体反向散射的螺旋桨噪声称为体积散射自噪声。
1.1.1 体积散射自噪声理论模型
某一时刻的噪声信号通过不同散射路径在同一时刻到达鱼雷头部声呐才能进行叠加。此时双程散射路径长度相等,不同散射路径形成的轨迹为椭球面。
使用以O为原点的直角坐标系(x,y,z),S为螺旋桨位置,Q为鱼雷头部声呐,它们是椭球的焦点。体积散射自噪声几何模型如图2所示。
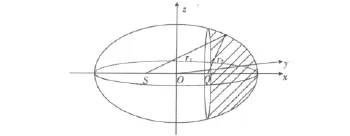
图2 体积散射模型坐标系Fig.2 The spherical coordinate of volume scattering model

设I0为距离噪声源1 m处的声强(SNL=10 logI0)。按照球面波传播规律,体积散射自噪声为

体元的选法:计算中体积散射微元是在椭球面上进行划分的。椭球面的大小只与噪声信号传播时间t/传播距离a有关,且由于螺旋桨噪声的连续性,T时刻产生的界面散射自噪声是由0~T内的噪声信号叠加形成的,即界面散射自噪声区域为椭圆面层叠加成的椭球体,那么层厚选为da,如图3所示。即体积散射自噪声为
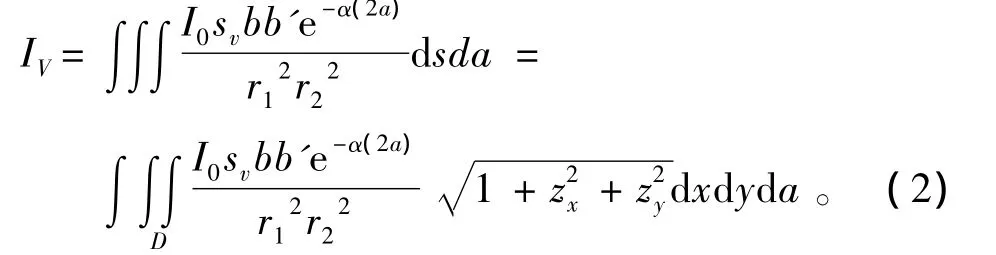

图3 体积散射体元Fig.3 The volume scattering element
1.1.2 体积散射自噪声预报
根据假设,b(θ,φ)=b'(θ,φ)=1,且考虑遮蔽效应,只算前向噪声,如图2所示的阴影区。体积散射自噪声为
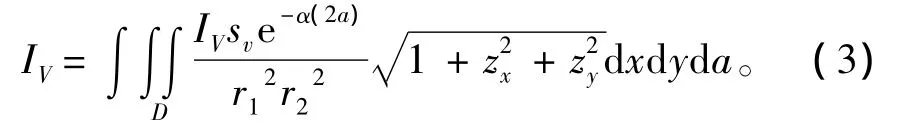
e2∂r按泰勒公式展开前3项,式(3)通过计算积分[9]得到:

体积散射自噪声级为
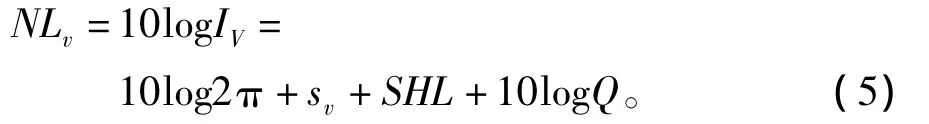
其中,

当观测距离增大时,椭球体近似于球体,相当于收发同置声呐的情况(L=0时)。
体积散射自噪声为

体积散射自噪声级为
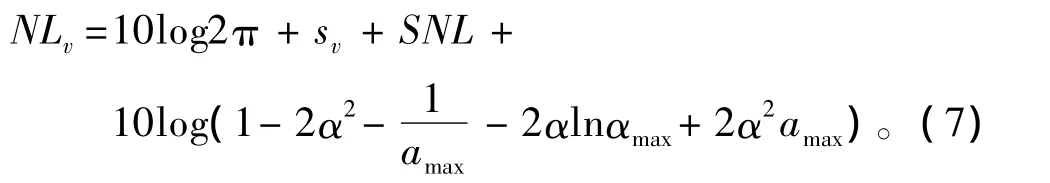
1.2 界面散射自噪声
螺旋桨噪声通过分布在界面上的散射体散射所形成的自噪声为界面散射自噪声。最显著的散射界面是海面和海底。
1.2.1 界面散射自噪声理论模型
椭球与界面相交的曲线为椭圆 (见图4),其方程为

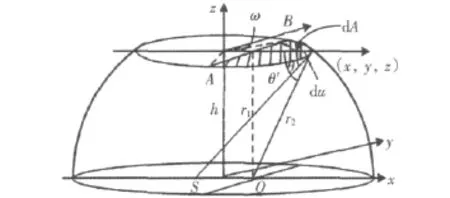
图4 界面散射模型坐标系Fig.4 The Spherical Coordinate of surfaee seat tering model
根据球面波传播规律,界面散射自噪声为

界面散射区域面元的选取:椭球面的大小只与噪声信号传播时间t/传播距离a有关,椭圆面的大小与传播距离a及航行深度h有关,即只与u有关。且由于螺旋桨噪声的连续性,某一时刻T产生的界面散射自噪声的区域是由0~T内噪声信号叠加成的,即为椭圆曲线叠加成的椭圆面,如图4中的阴影区。
1.2.2 界面散射自噪声预报
粗糙表面对声的散射满足Lambert定律随角度变化的函数。即界面散射系数为
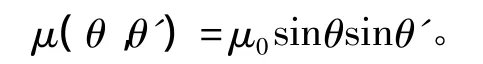
其中:θ为入射声波与界面之间的夹角;θ'为散射声波与界面的夹角;μ0为界面散射常量。
椭圆的2个焦点是收、发平台的2个点;椭圆的大小与信号传播路径a/时间t有关,椭圆曲线叠加形成的椭圆。
采用椭圆参数坐标,计算积分[9]得界面散射自噪声为

当L=0时,可得界面散射自噪声为

界面散射自噪声级为

其中,
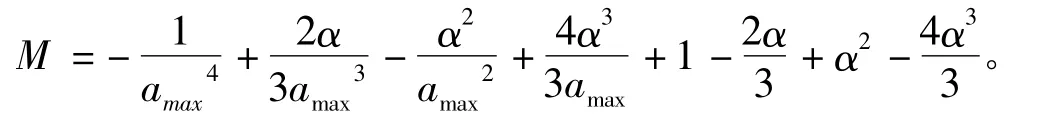
2 仿真分析
2.1 鱼雷自噪声仿真预报
仿真条件:假定海深100 m,鱼雷航行深度H=40 m,鱼雷辐射噪声级10logI0=108 dB。体积散射系数10log sv=-80 dB,界面散射常量10log μ0=-30 dB(海面),10log μ1=-20 dB(海面)。
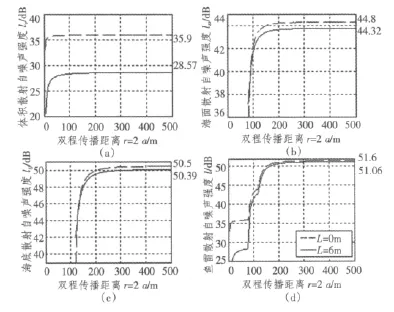
图5 散射自噪声随传播距离的变化关系Fig.5 The variation rule of scattering noise intensity with the change of propagation distance
从图5可看出,由于海底散射系数大,鱼雷散射自噪声中海底散射自噪声占主要地位。噪声信号传播到大约150 m左右的距离时,即鱼雷尾部噪声产生t=0.2 s后,头部声呐接收到的噪声强度达到某个定值,这个值即为散射自噪声强度,该值与国内外公开发表的现役鱼雷自噪声级相符,表明公式推导的正确性。
同时可以看出,在设定海深情况和航行深度的情况下,雷长L对体积散射自噪声影响较大。这是因为越靠近噪声源附近,散射距离越近,此时形成的散射自噪声影响大;当散射距离增大时,此时的散射自噪声的贡献越来越小。考虑雷长时,对体积散射自噪声影响最大的噪声源附近的噪声信号没有到达头部声呐,但对界面散射自噪声影响不大。
2.2 鱼雷散射自噪声与参数的关系
改变鱼雷辐射噪声级、散射系数、声吸收系数以及航行深度H等参数,进行计算机仿真,研究体积散射、界面散射及鱼雷散射自噪声强度随参数变化的规律。
2.2.1 散射自噪声与螺旋桨辐射噪声的关系
各种鱼雷在25 kHz的辐射噪声谱级与航速的函数关系,其随航速增加而增加,鱼雷散射自噪声也相应增加。仅改变辐射噪声级,得出表1的结论。
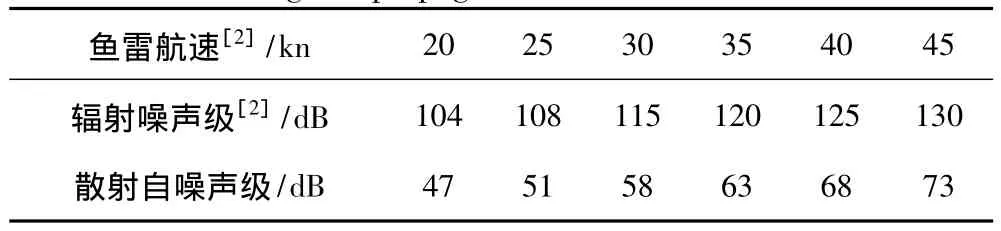
表1 鱼雷散射自噪声随螺旋桨辐射噪声级的变化规律Tab.1 The variation rule of the scattering noise intensity with the change of propagation distance
从表1数据可知,鱼雷散射自噪声与辐射噪声级成正比关系。
2.2.2 声吸收系数
仅改变声吸收系数,在上述条件下进行仿真:
α1=0.14 dB/km(纯水),
α2=2 dB/km(海水,温度为80°F),
α3=4.4 dB/km(海水,温度为60°F),
α4=6 dB/km(海水,温度为40°F)。
图6分别为体积散射、海面散射、海底散射及鱼雷散射自噪声随声吸收系数变化的关系。由于温度和盐度不同,海水声吸收系数不同,散射体积自噪声随声吸收系数的增大而减小。这是因为声吸收系数越大,噪声信号在海水中的衰减越大。

图6 鱼雷散射自噪声随声吸收系数的变化规律Fig.6 The variation rule of volume scattering noise intensity with the change of the scattering coefficient
2.2.3 散射系数
仅改变散射系数,在上述条件下进行仿真。
1)体积散射系数
体积散射强度大约在-70~-90 dB/km之间[2]。

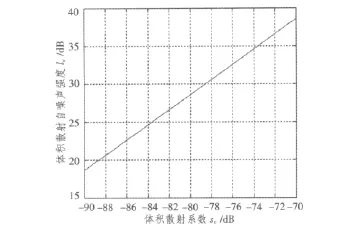
图7 体积散射自噪声随体积散射系数的变化关系Fig.7 The variation rule of volume scattering noise intensity with the change of sailing depth
2)界面散射系数
仅改变海面、海底散射系数,在上述条件下进行仿真,得出表2和表3的结论。

表2 海面散射自噪声随散射系数的变化规律Tab.2 The variation rule of sea surface scattering noise intensity with the change of the scattering coefficient

表3 海底散射自噪声随散射系数的变化规律Tab.3 The variation rule of sea floor scattering noise intensity with the change of the scattering coefficient
从表2和表3的数据可知,界面散射自噪声与散射系数成正比关系。
2.2.4 航行深度
仅改变航行深度,在上述条件下进行仿真。
图8(a)为体积散射自噪声随航行深度的变化规律。根据球面扩展定律,靠近鱼雷声呐的辐射噪声强度较远距离的大,当鱼雷航行靠近海面或海底时,因为海面或海底的影响,靠近声呐附近的散射体积小,所以产生的体积散射自噪声相应的就小。由图8可以看出,鱼雷辐射噪声信号扩展到靠近声呐附近10 m内的辐射噪声强度对体积散射自噪声强度的影响较大。当鱼雷航行远离海面或海底一定距离时,入射噪声强度Iinc对体积散射自噪声强度影响已经可以忽略,散射噪声强度Iscat=sv·Iinc·dV,尽管散射体积dV在变大,但此时因体积散射引起的自噪声强度亦可忽略。由此可见,体积散射自噪声强度只在鱼雷航行距离海面或者海底10 m内时会发生变化。

图8 散射自噪声随航行深度的变化规律Fig.8 The variation rule of volume scattering noise intensity with the change of sailing depth
图8(b)和(c)为界面散射自噪声随航行深度的变化规律。鱼雷航行距海面越近,海面散射自噪声小;鱼雷航行距海底越近,海底散射自噪声就越大。这是因为靠近鱼雷声呐的辐射噪声强度较远距离大,当鱼雷航行远离海面或海底一定距离时,辐射噪声Iinc减小,Iscat=∫μ·Iinc·dA,界面散射面积在变大,因为界面散射系数大,此时因界面散射引起的自噪声强度减小。
图8(d)为鱼雷散射自噪声随航行深度的变化关系曲线。海面、海底散射是主要影响因素。当海面散射自噪声大于海底时,海面散射自噪声占主要地位;反之,则海底散射自噪声占主要地位。
3 结语
基于双基地的声散射模型对鱼雷自噪声进行理论建模分析,推导出体积散射、界面散射自噪声及鱼雷自噪声理论预报公式。对鱼雷自噪声进行仿真研究,讨论了鱼雷自噪声随不同参数的变化规律。仿真结果表明,本文理论模型得出的鱼雷自噪声符合客观规律和现役鱼雷自噪声强度范围,该理论模型是有效的,这种思路和方法也是可行的,对高频、高航速下鱼雷自噪声的预报有实际意义。
[1]WSITE A D.实用声呐工程[M].王德石,译.北京:电子工业出版社,2004.79-111.
[2]尤立克 R J.水声原理[M].洪申,译.哈尔滨:哈尔滨船舶工程学院出版社,1990.190-240.
[3]惠娟,王自娟,惠俊英,等.双基地混响平均强度理论及仿真预报[J].物理学报,2009,58(8):5491-5499.HUI Juan,WANG Zi-juan,HUI Jun-ying,et al.The theoretical and simulation prediction of bistatic reverberation average strength[J].Acta Physica Sinica,2009,58(8):5491-5499.
[4]王国治,温华兵.鱼雷结构振动传递特性的试验研究[J].实验力学,2001,16(2):188-195.WANG Guo-zhi,WEN Hua-bing.An experimental investigation on the vibration transmission property of torpedo structure[J].Journal of Experimental Mechanics,2001,16(2):188-195.
[5]杜向党,秦丽萍,石秀华.鱼雷头部自噪声计算方法[J].弹箭与制导学报,2006,26(3):140-145.DU Xiang-dang,QIN Li-ping,SHI Xiu-hua.Computing method for the self-noise of torpedo[J].Journal of Projectiles,Pockets,Missiles and Guidance,2006,26(3):140-145.
[6]陈春玉,易红,郝保安,等.鱼雷发电机噪声对自导系统的干扰及其抗干扰技术[J].鱼雷技术,2007,15(6):1 7-19.CHEN Chun-yu,YI Hong,HAO Bao-an,et al.Influence of noise from torpedo electric generator on homing system and countermeasures[J].Torpedo Technology,2007,15(6):1 7-19.
[7]赵加鹏,石秀华,杜向党.鱼雷流噪声的综合预报方法研究[J].鱼雷技术,2009,17(2):10-14.ZHAO Jia-peng,SHIXiu-hua,DU Qiang-dang.An integrated prediction method of torpedo flow noise[J].Torpedo Technology,2009,17(2):10-14.
[8]李国付.鱼雷自导作用距离估算方法[D].西安:西北工业大学,2007.16-30.
[9]埃伯哈德,蔡德勒,等.数学指南[M].北京:科学出版社,2012,138-210.
