区域防空武器系统可靠性建模与仿真

魏 勇，黄 波，王新华，衡 辉

(海军潜艇学院导弹兵器系，山东青岛266042)

0 引言

武器装备作战效能的一个重要性能是可靠性，即武器装备在规定的使用条件下完成规定任务的能力。目前，对可靠性的研究主要集中在系统可靠性计算解析公式已知的情况下，对单个装备或系统可靠性研究及评估方法与算法方面。如文献［1-3］分别对导弹武器系统、舰艇的推进系统及火箭炮的发射系统的可靠性进行研究。文献［4］提出了基于事件模块的可修K/N(G)系统可靠性指标仿真算法。文献［5］研究了基于Bayes观点的系统可靠性评估方法。文献［6］给出基于单元参数渐近分布的渐近正态方法。

尽管上述研究取得了大量的研究成果，但如何研究复杂的、多样化的武器装备组成系统的可靠性，仅仅将针对单体或部件的可靠性分析方法，直接移植到对复杂系统可靠性的分析是不够的。因此，必须建立复杂系统可靠性相关理论与分析方法。本文通过对假想的区域防空武器装备系统进行分析，建立了区域防空装备系统的典型任务想定、装备系统组成想定和可靠性框图，通过蒙特卡罗仿真的方法研究系统可靠性的建模与仿真。文献 ［7］为研究提供了新的思路和方法。

1 防空系统组成及任务

1.1 系统组成

设定的区域防空体系如图1所示。假想敌轰炸机群要对目标进行轰炸，防空体系由3个层次的防御系统构成防空网络，对象分别是预警机、战斗机A、战斗机B、远程导弹A、远程导弹B、高射炮和地面雷达组成的防空体系。具体的层次结构如下:预警机和地面雷达站构成侦察体系;远程地空导弹阵地A和远程地空导弹阵地B成第1层次的防御体系;战斗机群A和战斗机群B构成第2层次的防御体系;高炮阵地构成第3层次的防御体系。

预警机和地面雷达组成并联的空-地侦察体系，共同对敌方目标进行侦察。远程导弹、战斗机群和高射炮组成的3层防御体系在时间上是有先后顺序的，在逻辑上是有触发关系的，其中，预警机或地面雷达发现敌机目标后，调动远程导弹A和远程导弹B执行拦截任务，如果拦截不成功则调动战斗机A和战斗机B进行空中格斗;如果任务依然失败了，就调动高射炮进行最后一层次的拦截。系统战斗工作过程主要工作状态及相关工作单元如表1所示。

表1 区域防空体系工作状态与相关工作单元Tab.1 Working state and correlative units of ZADWS

1.2 系统任务描述

系统任务是指防空系统每天执行规定时间的预警、防空任务，对可能的来犯敌机进行拦截并予以击毁，阻止敌机对我保护目标的轰炸。

任务是由各个作战单元任务按照一定的逻辑关系组合而成。各个作战单元的具体任务分工不尽相同，但每个作战单元的任务都有着一定的逻辑关系，描述如表2所示。

表2 区域防空武器系统任务描述Tab.2 Mission description of ZADWS

2 防空系统可靠性仿真模型

2.1 防空系统可靠性逻辑框图

整个区域防空任务是由预警机任务、地面雷达任务、远程导弹A(B)任务、战斗机A(B)任务和高射炮任务组成。预警机与雷达是协同工作关系，认为体系中一个系统工作，任务就可以执行，因此预警机与雷达可以看作可靠性并联系统;导弹、战斗机和高炮在执行任务上是先后关系，可以看作可靠性并联系统;侦察体系与防御体系之间是可靠性串联系统。整个系统的可靠性逻辑组合关系如图1所示。

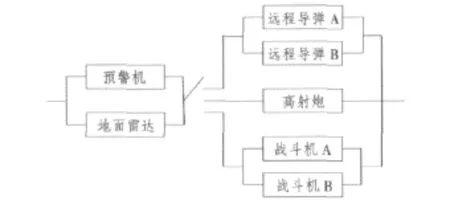
图1 区域防空武器系统可靠性逻辑框图Fig.1 Reliability logic diagram of ZADWS

2.2 子系统可靠性分布模型

子系统i的可靠度Ri(t)一般可由理论推导或实验统计得出。本文中假设各子系统可靠性分布模型如下:

1)体系中，预警飞机和地面雷达系统以电子器件为主，为不失一般性，可以假设其失效时间服从负指数分布，即系统i的开始工作时间，则系统Ti的可靠性为

式中λi为系统i的平均故障率。

2)导弹、战斗机均为短时间工作设备，取其一次工作成功率为可靠性指标，其分布函数服从二点分布，即

式中Pi为子系统一次工作成功率。

3)高炮是高强度、大应力环境条件下的工作设备，其设备故障分布函数为威布尔分布，工作的失效密度函数为

式中:m＞0，t0＞0，m为形状参数，t0为尺度参数;γ为位置参数，取常数。

系统可靠度为

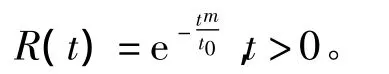
2.3 仿真统计模型

仿真利用离散事件驱动的仿真引擎模拟执行体系中装备使用的活动，自动推进任务的实例。由于各装备都是不同概率分布的随机变量，每次仿真运行都要从这些概率分布中进行随机抽样，得到规定概率分布的抽样时间，以便获得该次仿真运行的实际参数。

假设仿真系统总运行时间为T，任务时间为t，最小统计时间单位为Δt，仿真总运行次数为N。在第i次运行中M个子系统中第j个子系统的失效时间抽样值为 tij(1≤i≤N，1≤j≤M)。

1)系统任务可靠度模型

任务可靠度是指产品在规定的任务剖面内完成规定功能的能力。其度量指标用任务可靠度表示，它是系统能持续完成作战与训练任务的能力。其数学模型为

任务成功与否与装备故障引起的停机时间和任务允许的停机时间有关。在随机模拟时，统计模型为

2)数理统计置信度模型

对于这种统计试验结果，须根据置信度计算参数的置信下限，由于母体分布为 ［0 1］分布且DX均未知，故其可靠性的置信下限模型如下:

设系统的任务可靠性为R，置信水平为1-α，其置信下限R为

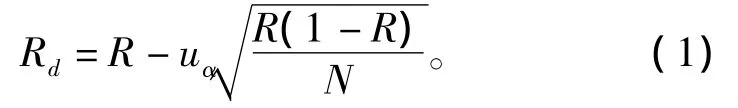
其中uα为α的标准正态分布的分位数，当置信水平为90%时，uα=1.28。

3 可靠性仿真实例

3.1 仿真原理与流程

对离散事件系统的仿真可采用Monte-Carlo法［8］产生随机事件，通过事件驱动仿真系统的运行过程，仿真原理如图2所示，仿真流程如图3所示。

3.2 仿真结果

表3给出了区域防空系统各子系统主要任务参数及根据系统的使命任务，以及确定的系统可靠性要求参数。

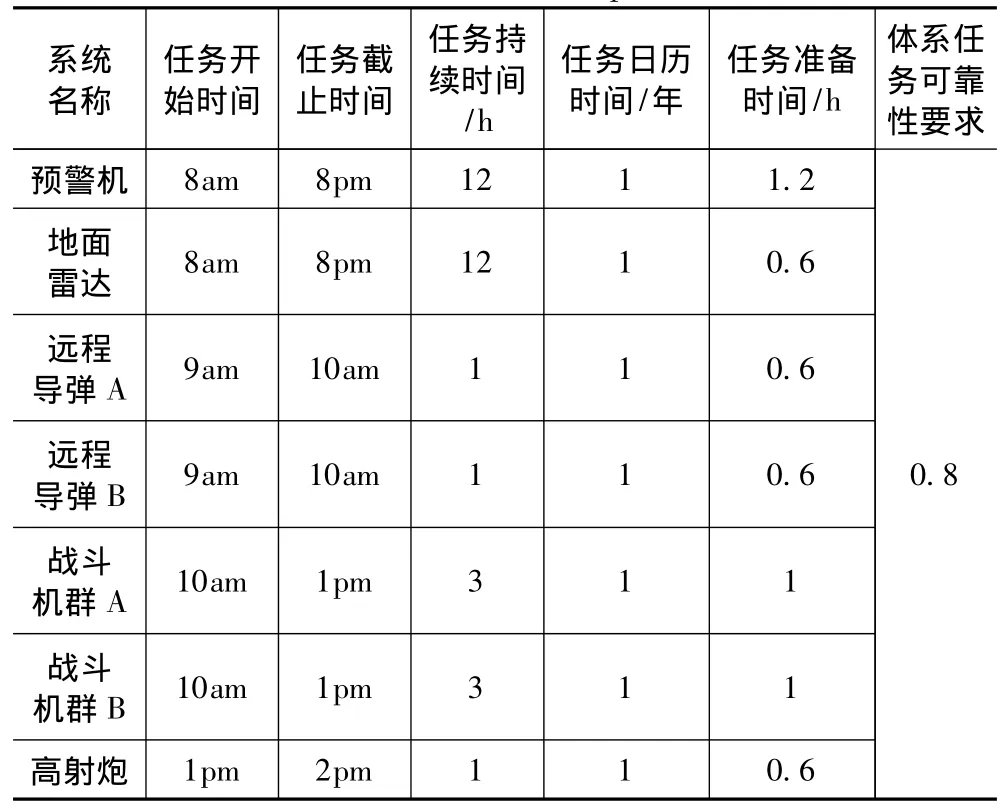
表3 任务参数Tab.3 Table3 Mission parameters

表4为在一定的任务时间及系统的可靠性数据等约束下，通过仿真得出的各子系统的任务可靠性。由于是统计试验，仿真中每50次试验统计1次输出参数，如果这次输出的“任务可靠性的置信下限”参数大于“规定的任务可靠性要求”参数，模拟结束，否则进行下1个50次统计。

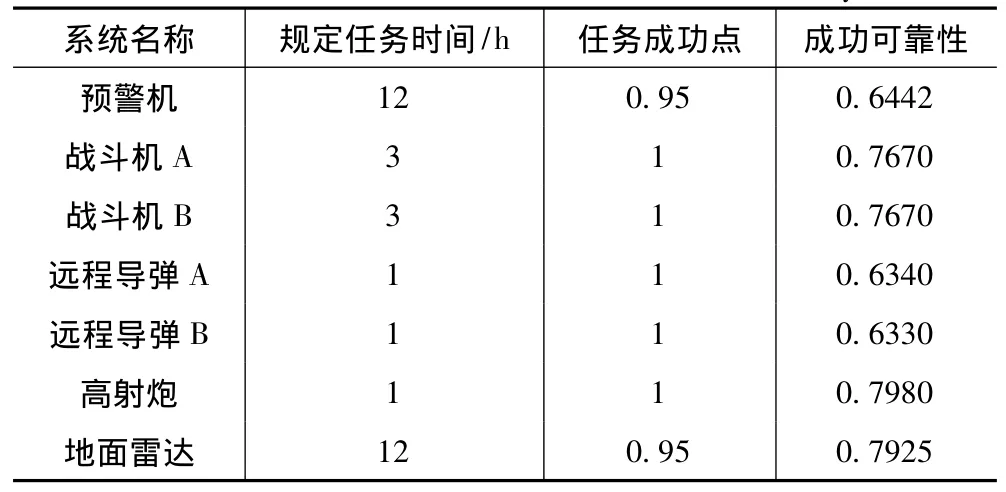
表4 任务可靠度仿真结果Tab.4 Simulation results of mission reliability

根据3层防御体系中各武器装备任务的逻辑组合关系，由图1所示可靠性框图关系，根据各个系统的任务可靠度，可以计算出3层防护体系拦截敌机总的任务可靠度

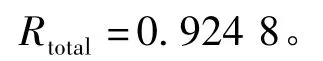
由式(1)可得任务可靠度的置信下限

结果说明，区域防空体系在该任务想定下，任务可靠度为0.924 8，任务可靠度的置信下限为0.877 06，满足任务可靠性0.8的使用要求。

图4是仿真50次时的频数直方图。从图中可以看出，在工作时间段的中部有一个明显的突起，这是因为此处导弹、飞机的可靠性模型采用的是两点分布，而且越是任务后期，由于涉及子系统增多，整个系统故障率增加，这和工程经验是一致的。

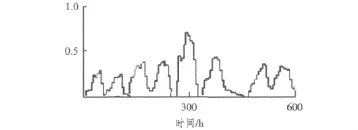
图4 频数直方图Fig.4 Frequence

4 结语

区域防空体系可靠性仿真的结果主要取决于体系中各组成装备的可靠性模型及其参数的合理性。本文是把体系中的装备看作一个整体进行求解，要使仿真结果更精确，需要将装备分解成子系统、部件，通过建立部件、子系统的可靠性模型，可以使得装备的可靠性模型得到细化，这样仿真结果可以越来越精确，才能提高区域防空体系的整体可靠性，而这项研究将是一项重要和长期的任务。

［1］辛永平，李为民.一种典型防空导弹武器系统可靠性模型及仿真实现［J］.系统工程与电子技术，2003，25(3):316-319.

［2］杨卫英.某舰主推进系统任务可靠性研究［J］.船舶，2005(5):41-43.

［3］罗辉，周建平，王德群.某新型火箭炮发射系统的可靠性分析［J］.四川兵工学报，2008(1):63-65.

［4］陈砚桥，金家善.可修K/N(G)系统可靠性指标的仿真算法研究［J］.计算机仿真，2008，25(11):115-118.

［5］SPRINGER M D，THOMPSON W E.Bayesian confidence limits for the product of cascade exponential systems［J］.IEEE Trans Reliability，1967，R16(9):86-89.

［6］HARTER H L，MOORE A H.Asymptotic variances and covariance of maximum likelihood estimators［J］.Annal Mathematical Statistics［J］.1967，38(4):557-570.

［7］巩军，黎放，刘平.基于PMS理论的常规潜艇任务可靠性研究［J］.舰船电子工程，2008，28(7):166-168.

［8］肖刚.动态系统可靠性仿真的五种蒙特卡罗方法［J］.计算物理，2001，18(2):173-176.