叶身/端壁融合技术研究
2012-09-28季路成李伟伟伊卫林
季路成,田 勇,李伟伟,伊卫林
(1.北京理工大学宇航学院,北京 100081;2.中国科学院工程热物理研究所,北京 100190;3.中国科学院研究生院,北京 100190)
0 引言
叶轮机内普遍存在复杂角区流动,其引起的性能恶化是叶轮机气动问题的主要部分。类比外流领域,叶轮机内并未选择“翼身融合”以消除这种影响,而是在不同指导思想下展开了实践探索,其中1类是采用弯叶片[1],利用弯叶片产生叶片体力特殊分布以实现二次流动控制、改善性能。但同时也产生了“正弯好还是反弯好”的疑惑和缺乏实施准则的问题。叶轮机中另1类受重视的角区问题发生在叶片前缘与端壁相交区域,不过,相关研究一直将此视为壁面上障碍物绕流问题而孤立地关注马蹄涡的产生、发展和影响、控制问题。一些研究者将前缘处修型为凸包,用于增强前缘马蹄涡的吸力侧分支以削弱通道涡,如2000年Sauer等[2]的工作;Zess等[3]的研究则关注修改前缘形状以直接削弱马蹄涡。此外,研究者还更多孤立关注端壁附面层内横向二次流影响,提出了非轴对称端壁技术[4-7]。
本文基于二面角原理,借鉴外流翼身融合,以及综合叶轮机非轴对称端壁技术,提出了叶轮机叶片(身)/端壁融合技术(BBEW)[8]。以NASA 67号转子叶片为例,采用数值方法验证该技术在减弱或消除角区分离方面的有效性。研究不包含已经广为研究的非轴对称端壁,仅局限于叶片与端壁连接处以光滑曲面过渡,而其特殊情况——以适当大倒圆过渡,与通常工艺倒圆并不相同,倒圆半径一般沿流向保持不变,仅仅是出于避免应力集中等纯结构工艺方面的考量。
1 二面角原理
二面角概念最早由Smith[9]在1963年与掠概念同时提出,Lewis[10]进行了2者在叶轮机应用的研究,但是,关于二面角对流动影响机理与使用规律,相关文献一直未给出深入明确阐释。在以后的发展历程中,掠叶片技术在20世纪90年代中后期取得突破性进展,尽管有关联,弯叶片技术关注点却与二面角渐行渐远,由此产生“正弯好还是反弯好”的疑问,导致公开文献中二面角尚未直接应用于指导设计的局面。
2006年,从二面角决定相交固壁附面层形态这一认识出发,基于流动堵塞和损失厚度的几何假设,Ji[11]给出描述角区3维附面层的等效2维附面层模型,并结合2维附面层分离准则,建立了固壁交汇角区分离判定准则,继而提出了以二面角视角控制角区流动的规律。
事实上,在Ji[11]所述二面角原理中,固壁交汇角区流动形态经由综合3个附面层方程来描述,即

式中:H为形状因子;Mae为主流马赫数;Cf为摩擦系数;α为叶表与端壁相交的二面角;x为流动方向。
对上述角区所涉及的3类附面层引用文献[12]中的准则进行分离预测,即

任何1类附面层被判别为分离都意味着角区流动将发生分离,而分离点后的预测将由于严重偏离实际而不再被采纳。针对叶表附面层和端壁附面层,上述即是传统的叶轮机设计判据,而针对新建立的角区等效附面层,体现为上述分离准则式直接相关于二面角α,这将带来新的叶轮机设计判据。为此,将式(3)代入式(4)、(5)中,由考察角区内分离判据参数-(θef/ue)(due/dx)和 dθef/dx 沿叶表与端壁交线的变化规律得出
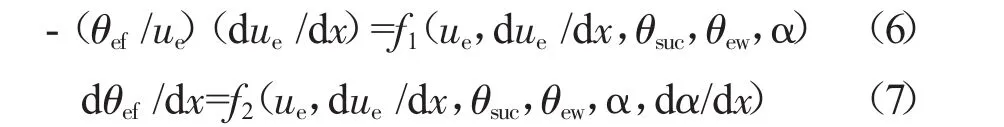
除了是主流速度ue、速度流向梯度due/dx、叶表和端壁附面层动量损失厚度(θsuc,θew)的显函数,分离判据参数还是二面角α及其流向梯度dα/dx的函数。也就意味着,可能通过调节二面角α及其流向梯度分布而避免分离

可以证明,对所有情况,df1/dα<0,因而表明,二面角α越小,等效2维附面层越容易分离,角区越容易分离。所以为避免角区分离,应使二面角α尽可能大。
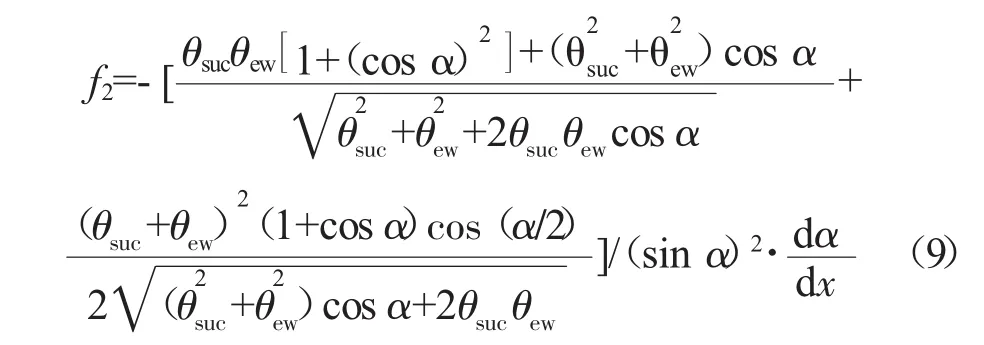
由上式可看出,dθef/dx与dα/dx间存在准线性关系,且比例系数始终为负数,因此,只有当dα/dx为负,即二面角α沿流向递减才有可能发生角区分离,而α变化梯度绝对值越大,角区也就越容易分离。因而,为避免角区分离,应使α沿流向逐渐增大,或者使α沿流向逐渐减小过程尽量平缓,尤其在α较小的区域更应如此。
2 二面角原理与叶身/端壁融合
二面角原理表明,在设计中通过监控和调整二面角大小及其流向变化率可以规避分离,而控制规律是增大和减小二面角流向变化梯度的绝对值。据此,二面角原理有以下3种应用方式。
2.1 增大二面角
根据二面角原理,增大二面角可以改善角区流动、抑制分离。为此,叶轮机设计中应在端区尽可能增大叶片与端壁相交二面角(如图1所示),这与流行的弯叶片技术具有某种程度的相近性,但弯叶片技术更强调通过弯改变叶片压力分布,继而改变二面角,减小损失,未能特殊关注角区流动,体现为尚未形成有关近端区叶片弯和尺度范围的经验。而根据二面角原理,增大二面角的展高区间尺度与当地附面层厚度尺度相当——这是难得的设计准则。
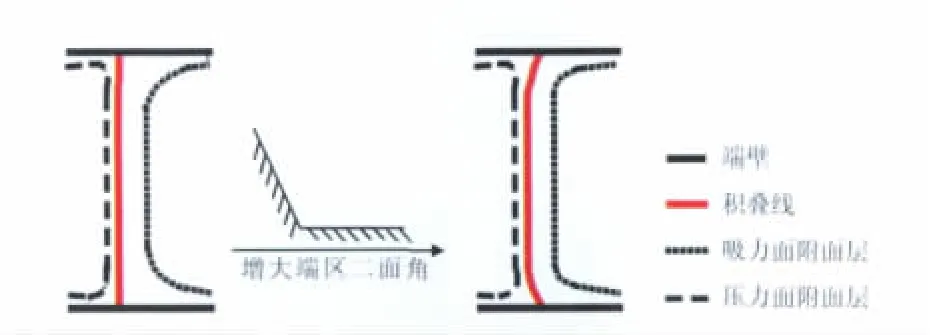
图1 增大二面角方式
2.2 增大过渡曲线(面)的最小曲率半径
在一些场合,叶片二面角增大便对应着其背面二面角减小,而且增加二面角自身就可能受到其他外在因素限制,如高负荷风扇根部。在这种局面下,将叶片表面与端壁以任意光滑曲线(面)过渡连接(这时相当于二面角变为180°),如图2所示,并置光滑曲线(面)最小曲率半径至少与当地附面层最大厚度尺度相当,同样可能达到改善流动效果。应该注意,这与通常的工艺倒圆在用途上完全不同,尽管有时由于过渡光滑曲线选为圆而形态相似,但沿环绕叶片与端区的交线,倒圆半径通常不变或简单线性变化,其用途主要是避免应力集中、提高叶片强度。
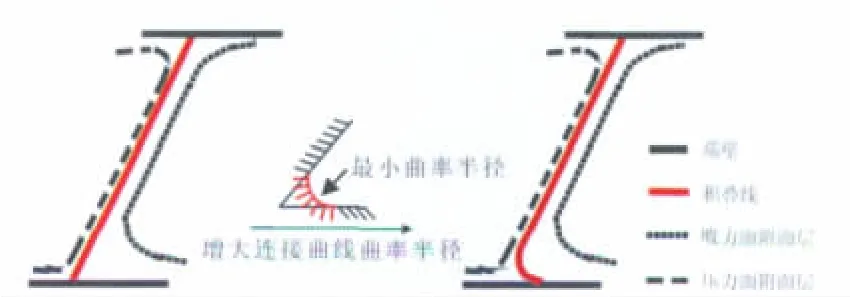
图2 增大最小曲率半径方式
2.3 减小二面角流向变化梯度
还有些情况,不是二面角不够大,而是其流向减小的梯度太大。例如高负荷风扇根部,根区叶片在弦长中点以后通常是二面角迅速减小而导致分离。针对这种情况,减小二面角变化梯度会大大改善流动。极端情况发生在与固壁相交钝体绕流上,如图3(a)所示,这时端壁附面层可看成为二面角为180°的交汇附面层,在遇到钝体障碍物时,这个附面层迅速分为交角之和为180°的2股角区流动,角区二面角由180°在极短距离内变为互补的钝角和锐角,二面角变化梯度趋近无穷大,导致流动分离卷起,即形成马蹄涡。根据该认识,改造钝体与端壁相交过渡形式,使二面角流向变化梯度为有限值,结果是马蹄涡被大大削弱甚至消除,如图3(b)所示。

图3 控制二面角流向梯度方式
除继承非轴对称端壁以部分控制横向二次流外,从内涵看,叶身/端壁融合技术主要包含上述二面角原理的3种应用方式:(1)针对第1种方式,主要依靠调整叶片积叠轴使叶片吸力面与端壁尽可能成钝角相交;(2)如果受外在条件限制而使得第1种方式不可为时,则采用第2种方式,用光滑曲线(面)过渡连接吸力面和端壁;(3)针对前缘与端壁交汇处,则采用第3种方式,对叶片前缘采取前伸光滑曲面方式,使二面角随流梯度由无穷大减为有限小值。3种处理方式的几何特征尺度均与当地附面层厚度尺度直接关联。
限于篇幅,本文仅研究叶身/端壁融合的第2种方式,即增大过渡曲线(面)的最小曲率半径。
3 数值研究
3.1 数值模型选择
据负荷与叶片折转内在关联,在端区负荷较高时更可能出现二面角较小或其沿流递减梯度较大情形。由此,叶身/端壁融合更多会在高负荷叶片内清楚展示其效益。为清晰证实叶身/端壁融合技术效果,选用合适的数值模型非常关键。
NASA 67转子叶片是NASA设计并试验的低展弦比跨声速轴流风扇动叶,已作为高负荷跨声速风扇/压气机流动机理研究和CFD校验的典型案例使用。该转子叶片根区近尾缘吸力面与端壁间存在的分离现象是其中重要特点,这已在研究中得到广泛证实[13],如图4所示。参数化分析表明,转子叶片根区表面与端壁所交二面角形成如图5所示流向分布,在吸力面侧,二面角从前缘附近约110°到中弦处开始迅速降为尾缘处约60°,在逆压梯度较大的后半部恰恰是二面角流向减小梯度较大的区域,按照前述准则,这也是最倾向于分离的区域。因此,在67转子叶片上实施叶身/端壁融合技术最有可能展现其应用效果,这是以下选用67转子叶片(原型)及其改型(实施叶片/端壁融合后简写为BBEW改型)作为本研究数值模型的初衷。

图4 Chima[13]计算所得67转子叶片根区分离情况

图5 67转子叶片根区叶表与轮毂端壁二面角分布
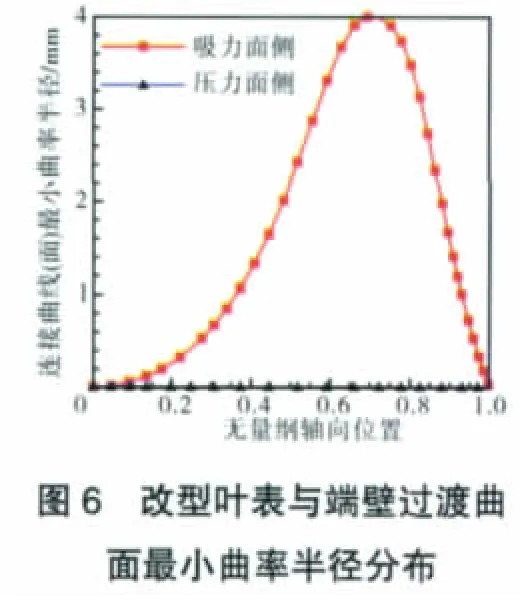
同时,尽管完整的叶片/端壁融合专利[8]技术在端壁形式方面可以继承非轴对称端壁,但鉴于相关研究已比较深入,且本文更关注叶身与端壁交汇角区,改型过程因而仅涉及用光滑曲线(面)连接吸力面和端壁以增大二面角。从图5中可见67转子叶片根区二面角流向分布,并考虑压力面与吸力面侧差别、前缘/尾缘处应与原型一致等,按如图6所示规律给定叶表与端壁过渡光滑曲线(面)最小曲率半径沿流程分布,形成67改型叶片与端壁如图7所示。本研究中尚未对叶表与端壁过渡光滑曲线(面)最小曲率半径沿流程分布进行优化,这是后续深入研究和应用努力的方向。

3.2 数值研究方法
针对67转子叶片原型及其BBEW改型,采用ANSYS-ICEM生成结构化网格,如图8所示。为确保模拟质量,网格生成过程既考虑了叶尖间隙,也保证了近壁网格间距Y+<20~50以可靠描述附面层;同时为确保比对结果合理有效,对这2个算例均采用相同网格拓扑结构,并保持网格疏密一致。根据单排单通道流动模拟的网格依赖性研究结果,将计算总网格数控制在210万左右。
数值模拟基于N-S方程,并采用带扩展壁面函数k-ε模型对湍流相关项进行封闭。为使数值研究结果可采信、结论可靠,数值模拟均采用CFD商业软件ANSYS-CFX,并对原型进行了详细数值校验以获得正确的使用和评估经验。图9、10分别给出了100%转速下试验与数值计算结果的对比,包括总性能和详细的流动参数展向分布。由此可见,无论是总体性能参数还是流动参数的分布,计算值都与试验值符合很好,针对该软件、该算例的计算经验得以建立。

图8 计算网格
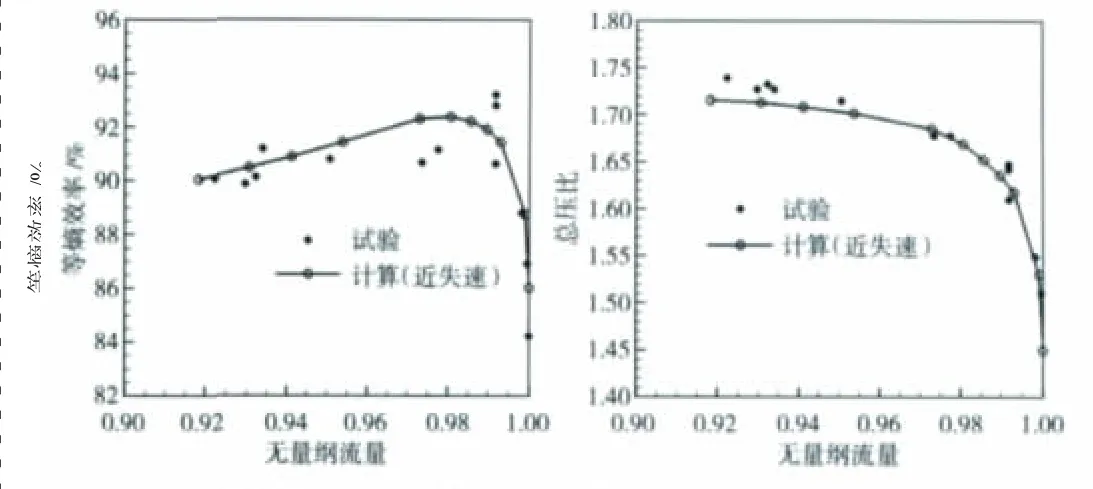
图9 效率与压比特性线的计算与试验对比(100%转速)
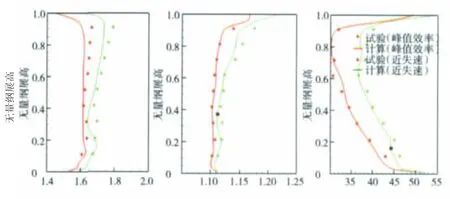
图10 峰值效率点与近失速点出口总温、总压、出口角展向分布的计算与试验对比(100%转速)
4 结果分析
对原型和BBEW改型进行了数值模拟。根据计算结果整理得到的压比和效率特性分别如图11、12所示。相对于原型,BBEW改型有略微的裕度优势但仍有待试验验证,在堵塞流量不变条件下压比略有增大、效率整体提高0.2~0.3个百分点。峰值效率点和近失速点效率的展向分布对比分别如图13、14所示。
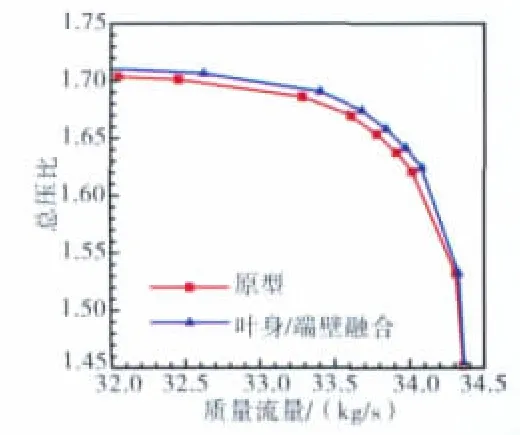
图11 原型和BBEW改型的流量-压比特性

图12 原型和BBEW改型的流量-效率特性

图13 峰值效率点的效率展向分布对比

图14 近失速点的效率展向分布对比
从图中可见,在峰值效率点,叶身/端壁融合使得转叶根区效率较原型有显著改善,甚至大部分展高的效率提高。需要解释的是,由于较大效率改善主要发生在根区,而根区流量比率低且基准效率已经较高(95%以上),因此,整体上显现的效率提升并不大。另外,未能优化也是效率提升有限的原因之一。
峰值效率点和近失速点绝对切向速度分量的展向分布分别如图15、16所示。从图中可见,采用叶身/端壁融合以后,根区20%展高内绝对切向速度分量大大增加(约10%),结合如图17、18所示的峰值效率点和近失速点子午速度变化较小的总体情况看,说明根区20%展高范围内流动落后角减小,在叶型未经改变情况下,叶身/端壁融合削弱附面层分离是产生这一效果的根本原因。
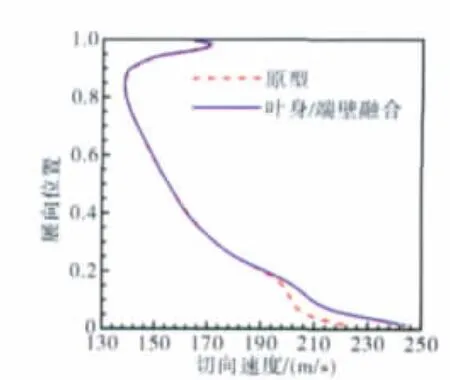
图15 峰值效率点的切向速度展向分布

图16 近失速点的切向速度展向分布
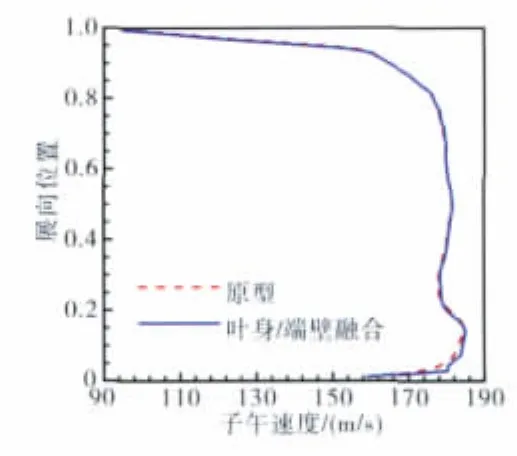
图17 峰值效率点的子午速度展向分布
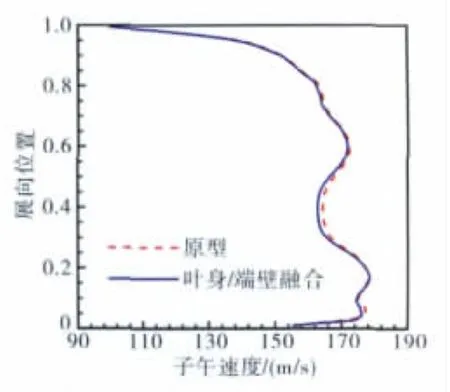
图18 近失速点的子午速度展向分布
峰值效率点和近失速点时叶片根部吸力面与轮毂端壁摩擦力线的分布对比分别如图19、20所示。从图中可见,在原型中,轮毂端壁附面层在冲向吸力面时与已经处于分离边缘的叶表附面层交汇,在靠近尾缘时已经无法自持,形成角区分离,表现为摩擦力线并未到达吸力面,而是汇聚形成分离线;与此形成鲜明对比,在BBEW改型中,近尾缘附近轮毂壁面上的摩擦力线光滑地移向叶表吸力面,而吸力面上附面层分离甚至角区分离已消失殆尽,表明端壁附面层冲向叶表吸力面时,顺带移除了叶表吸力面附面层中的低能流团,避免了已处于分离边缘的吸力面附面层继续走向失稳。从总体看,无论是在峰值效率点还是近失速点,BBEW改型均明显地削弱了近尾缘处根部角区分离,叶片后尾迹宽度明显减小。整个特性线上各工况点的流场检验均显现了这样的规律。

图19 叶片根部吸力面与轮毂端壁摩擦力线分布对比(峰值效率点)

图20 叶片根部吸力面与轮毂端壁摩擦力线分布对比(近失速点)
为更清晰认识叶身/端壁融合效果的机制,选择如图21所示S3-4和S3-6的2个流向位置的S3截面,观察其马赫数以及熵分布情况。原型和BBEW改型在S3-4、S3-6截面处等马赫线对比分别如图22、23所示。由图中可见,在S3-4截面,BBEW改型使吸力面与轮毂角区流动速度大大提高,到了S3-6截面,已经可以清晰看到,由于前面流速提高后,根部角区分离大大减小,体现为低速区范围显著减小。原型和BBEW改型在S3-4、S3-6截面处熵等值线进一步对比分别如图24、25所示。从图中明显可见,尽管原型和BBEW改型在S3-4截面处的熵分布几乎一致,但BBEW的作用在近尾缘处显露无遗:在S3-6截面处,不但根部高熵区(通常被称为尾迹区)厚度明显减小,熵的最大值也有所减小。
上述分析清楚表明:采用BBEW技术能够消除或削弱角区分离,是继续提高叶轮机负荷能力的重要技术途径。
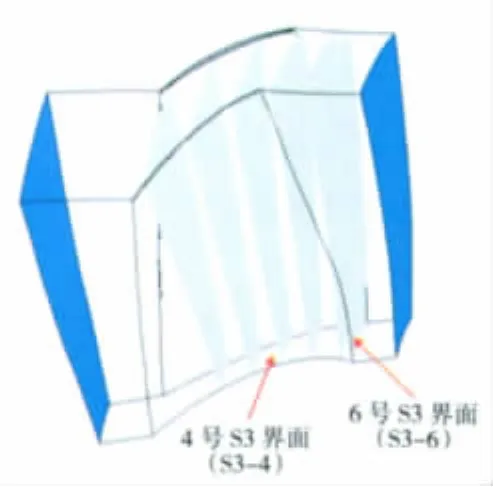
图21 S3-4和S3-6截面定义

图22 S3-4截面等马赫数线对比(峰值效率点)

图23 S3-6截面等马赫数线对比(峰值效率点)

图24 S3-4截面熵等值线对比(峰值效率点)

图25 S3-6截面熵等值线对比(峰值效率点)
5 结束语
本文首先回顾了二面角原理,继承了但不在本文讨论范围的非轴对称端壁技术,叶身/端壁融合技术包含了二面角原理的3种应用方式,其中第2种方式作为本文研究重点。为此,选择NASA67号转子叶片作为研究对象,实施了吸力面与轮毂端壁的光滑过渡。数值模拟结果表明:仅采用叶身/端壁融合技术中第2种二面角原理应用方式,即便还未经过详细优化,叶身/端壁融合已经能在几乎全部工况下消除根区吸力面侧角区分离,能够改善效率和压比等性能参数,是1种有前景的叶轮机负荷能力最大化技术途径之一,未来可能广泛应用于轴流/混流/径向压气机、涡轮、泵和风机等叶轮机械。
[1]Filippow G A,WANG Zhong-qi.The effect of flow twisting on the characteristics of guide rows[J].Teploenergetika,1964,11(5):54-57.
[2]Sauer H,Muller R,Vogeler K.Reduction of secondary flow losses in turbine cascades by leading edge modifications at the endwall[J].Journal of Turbomachinery,2001,123(2):207-213.
[3]Zess G A,Thole K A.Computational design and experimental evaluation of using a leading edge fillet on a gas turbine vane[J].Journal of Turbomachinery,2002,124(2):167-175.
[4]Deich ME,Zaryankin A E.Methods of increasing the efficiency of turbine stages[J].Teploenergetica,1960,7(2):18-24.
[5]Morris A W H,Hoare R G.Secondary loss measurements in a cascade of turbine blades with meridional wall profiling[R].ASME 75-WA/GT-13.
[6]Kopper F C,Milano R,Vanco M.Experimental investigation of endwall profiling in a turbine vane cascade[J].AIAA Journal,1981,19:1033-1040.
[7]Rose M G.Non-axisymmetric endwall profiling in the HP NGVs of an axial flow gas turbine[R].ASME 94-GT-249.
[8]季路成,伊卫林,田勇,等.一种叶轮机械叶片与端壁融合设计方法:中国,CN102094847A[P].2010-06-15.
[9]Smith L H,Yeh H.Sweep and dihedral effect in axial flow turbomachinery[J].ASME Journal of Basic Engineering,1963,85(3):401-416.
[10]Lewis R I,Hill J M.The influence of sweep and dihedral in turbomachinery blade rows[J].JournalofMechanical Engineering Science,1971,13(4):266-285.
[11]JI Lu-cheng,SHAO Wei-wei,YI Wei-lin,et al.A model for describing the influences of SUC-EW dihedral angle oncorner separation[R].ASME 2007-GT-27618.
[12]Nash J F,Macdonald A G J.The calculation of momentum thickness in a turbulent boundary layer at mach numbers up to unity[M].London:Aeronautical Research Council Current Papers,1967:963.
[13]Chima R V.Viscous three-dimensional calculations of transonic fan performance[C]//AGARD Conference proceedings CP-510,London:HerMajesty's Stationery Office,1991:80-103.
