1种新型增推喷管的数值研究

林 卉，李志强

（北京航空航天大学能源与动力工程学院，北京 100191）

0 引言

作为航空发动机的重要部件之一，喷管的性能对发动机的性能有着重要影响。如果喷管的面积比按设计降压比定出，则当喷管的工作状态发生变化时，其面积比就不再适应变化后的喷管降压比，使喷管处于不完全膨胀或过度膨胀状态，从而使喷管推力下降。为此，国内外的工程应用和机理研究主要集中在喷管喉道处通过机械或气动方式来控制喷管流量以适应不同的工作状态。而相比于机械调节造成的喷管结构复杂、质量大等缺点，射流控制技术从20世纪90年代开始得到了广泛关注[1-2]。与传统的机械式方案相比，射流方案具有机械部件少、质量轻、费用低等优点[3]。目前研究较多的射流方案主要有：激波操纵[4-5]、喉道偏移[6-7]以及在此基础上发展的双喉道偏移[8-11]和逆流控制[12]。而近年来在高性能喷管方面的研究大多集中于双喉道偏移产生矢量效应技术。国内在射流推力矢量技术方面的研究起步较晚，在双喉道喷管领域的研究还很少，一些高校的少许研究仍然集中在矢量效应方面，而对其增推原理尚未进行研究。

为了进一步研究射流控制技术对喷管内部流动和推力性能的影响，促进喷管出口射流控制技术的发展，本文将双喉道喷管的出口喉道设计为1个气动喉道，而不再是几何固体喉道，从而建立1种“固－气双喉道喷管”。利用数值模拟手段，探索该喷管出口处射流控制气动喉道对轴对称超声速收扩喷管性能的影响规律。

1 传统双喉道喷管

双喉道喷管（Dual-Throat Nozzle，简称DTN）是在传统的喉道偏移喷管后增加1个收缩段，形成1个凹腔（如图1所示），并在上游喉道处引入二次流扭曲了该处的声速面，通过凹腔内流动分离产生的上、下壁面压力差使主流进一步偏转。采用双喉道方案可以比采用传统的喉道偏移方案获得更大的推力矢量效率，且不减小推力系数。文献[9]的试验研究表明，在喷管落压比PRN=4时，该方案实现了最大为15°的推力矢量角，最大推力效率是6.1°/单位引射量，对应的推力比为0.968，与非推力矢量相比，推力损失小于0.5%。如此良好的表现使得双喉道喷管成为目前国内外航空界探索研究的热点，但该喷管的优势也仅仅局限在良好的矢量效果上，而却不能得到增推效果。

图1 双喉道喷管（DTN）结构

2 物理模型和计算方法

2.1 计算模型

本文的研究对象为小收扩比喷管[13]，其几何模型如图2所示。原始喷管几何形状如图2（a）所示，喷管出口面半径为0.01273 m，出口面积与喉道面积之比为1.055，具体几何尺寸见文献[13]。为了实现气固双喉道思想，在喷管出口处增加了1个二次流控制的气动喉道，如图 2（b）所示。

图2 喷管几何模型

2.2 计算网格

采用商用Fluent软件进行2维模拟，考虑对称性，计算网格为实际流场的一半，均为6面体网格，如图3（a）所示，网格数量约为4万个，在压力变化较大和近壁面处进行加密，使得壁面处的y+≤3，从而保证该网格质量满足SA湍流模型的需要。喷管气动喉道处的网格细化如图3（b）所示。

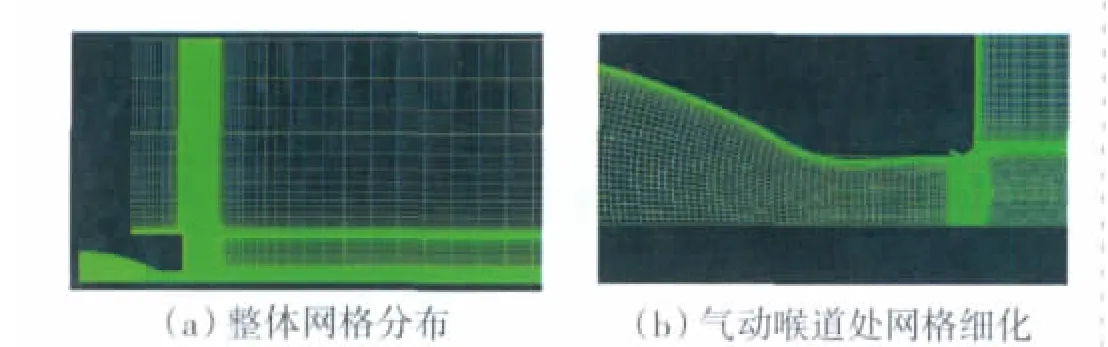
图3 计算网格

2.3 计算方法与边界条件

流场计算基于求解2维Reynolds时平均N-S方程。采用4阶R-K进行时间推进求解，对流项采用2阶迎风格式离散求解，黏性项采用中心差分格式求解。

主流为超声速流动，进口为压力进口，状态给定总压、总温、初始静压和速度方向。射流流动假设为均匀流动，进口也为压力进口。出口采用压力远场条件，假设壁面绝热无滑移。自由流马赫数为0.03，主次流入口总温为300 K，环境温度为297 K，环境压力为9.895 MPa，设计落压比PRN=3.16，二次流入口细缝长度为0.64 mm。

分别计算了不同二次流的压比（PRS）和喷射角度时的喷管推力性能。

2.4 参数计算

式中：Wip/is为主流/射流理论流量[16]；Wp/s为主流/射流实际流量；Ue为喷管出口速度；P9为出口静压；P0为大气压；A9为出口面积；A8为固体喉道面积；A10为气体喉道面积；为主流/射流进口总压；Ft1为射流后主流实际推力；Ft0为无射流时主流实际推力；X1为气体喉道与出口的轴向距离；D为喷管出口直径。

2.5 数值方法的验证

利用文献[13]的结果对所采用的计算方法进行验证。原始喷管出口轴线速度分布如图4所示，在无射流、PRN=3.16时，在喷管出口轴线速度分布的试验值和计算值吻合较好，表明本文所采用的计算方法比较精确，能用于固气双喉道喷管研究。

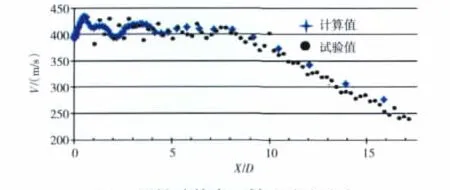
图4 原始喷管出口轴线速度分布

3 数值结果及分析

3.1 二次流压力对喷管性能的影响

喷管出口射流控制处形成气动喉道的二次流的压力对喷管出口主流流场、推力系数和流量系数的影响规律如图5、6所示。

从图中可见，在PRN=2.135时，对于主流流场来说，当二次流压比为0.8时，射流压缩主流作用开始明显，主流流量系数开始减小；当二次流压比增大至1.0时，由于主流压缩造成的流量系数减小7%，此时二次流所占出口流量增大。同时，随着二次流压比的增大，主流出口有效面积减小，扩张段超声气体被再次压缩，出口静压增大，当PRS＞0.7时，二次流能有效地在喷管出口处形成1个气体喉道，即喷管变成固-气双喉道喷管，可以通过调节气体喉道面积来有效控制出口截面的流动，从而增大喷管的推力系数。另外，随着气动喉道的形成，主流受环境作用的影响减弱，即有效减弱了主流和环境相互作用所产生的激波效应，从而进一步提升喷管的推力。在没有二次流所形成的气动喉道，即PRN=2.135、PRS=0时，喷管出口静压小于外界大气压，属于过膨胀状态，存在过膨胀损失，则其推力系数小于有气动喉道的喷管推力系数。

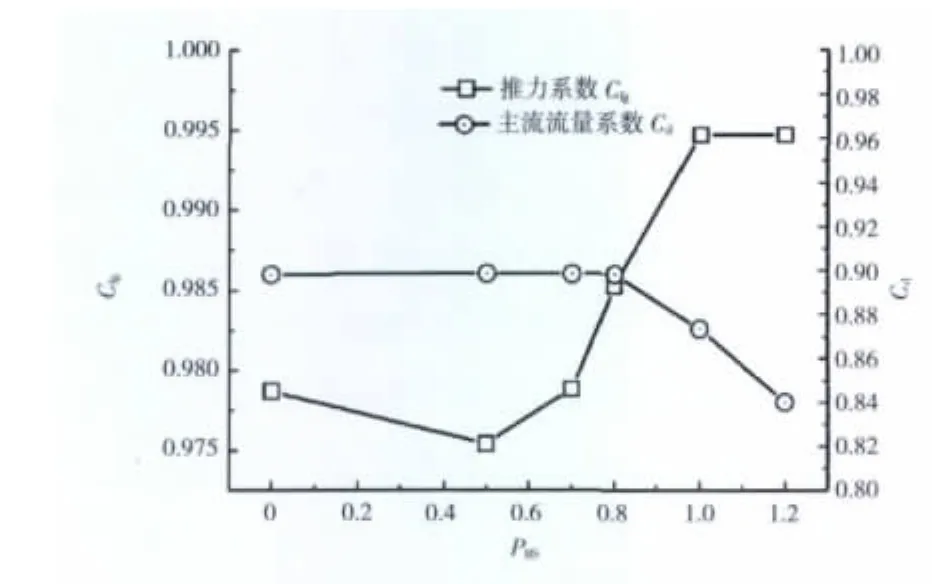
图5 推力系数和主流流量系数随PRS变化

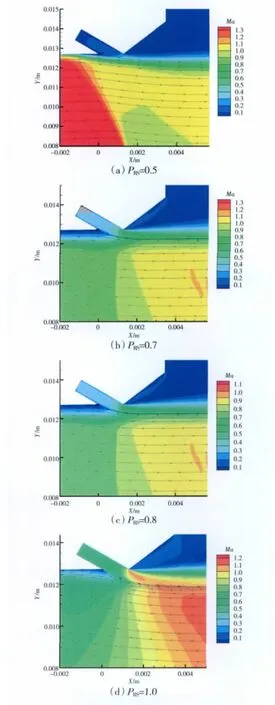
图 6 PRN=2.135、θ=30°时不同 PRS 主流流场

喷管轴线出口无量纲压力变化情况如图7所示。图中横坐标表示轴线远离出口距离X与出口直径D的比值，纵坐标表示轴线出口压力与环境大气压之比，2个参数均为无量纲数。从图7中可见，当PRN=2.135 时，在无射流情况下，即 PRS=0 时，P/P0＜1，即喷管出口压力小于反压，出口超声速气体受到强压缩产生激波，出口压力突然增大，气体经过激波推力有所损失，推力系数减小；当PRS=0.5时，出口为超声速，并且仍有激波出现；继续增大PRS时，主气流量也随之增加，激波前压力增大，因此激波强度减弱，激波往外移动，喷管出口处为亚声速，激波出现在外界大气中，并且随着PRS的增大，激波与出口截面的距离在增大，使得激波对喷管出口影响减小，推力系数随之增大。[14-15]

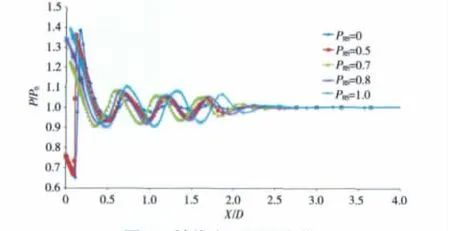
图7 轴线出口压强变化

3.2 二次流喷入角对喷管性能的影响

当PRN=2.135和PRS=0.7时，不同射流喷入角对主流流场的影响如图8所示。图中红色区域为超声区，蓝色区域为亚声区，中间分界线为声速线。当喷入角为30°时，主流被压缩；当喷入角增大到60°时，主流被明显压缩，出口有效面积减小，同时声速线靠近出口，出口速度增加，喷管出口激波被抑制，推力系数增大；而当喷入角增大到90°时，主流被压缩效果又变得不明显；喷入角继续增大到120°时，主流又重新被有效压缩，但此时声速线却向喷管出口处靠近，出口压力减小，推力系数增大但小于60°时的值。由此可见，顺向二次射流能获得更好的推力效果。射流喷入角影响主流流场，从而影响喷管性能的变化如图9所示。

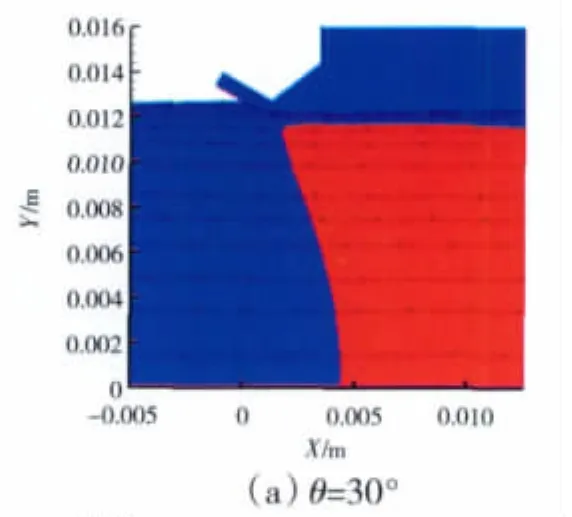
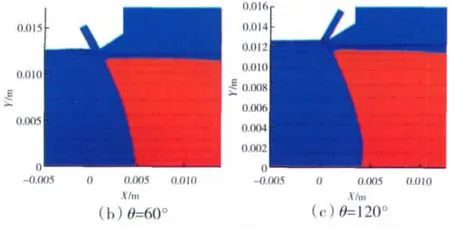
图8 PRN=2.135、PRS=0.7,不同射流喷入角时主流流场

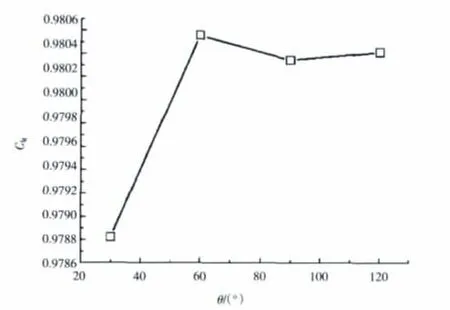
图9 PRN＝2.135、PRS=0.7时推力系数随射流喷入角的变化

3.3 气动喉道对喷管主流推力的影响

当PRN=2.135、θ=30°时，不同气动喉道位置和面积对喷管主流推力的影响如图10所示。

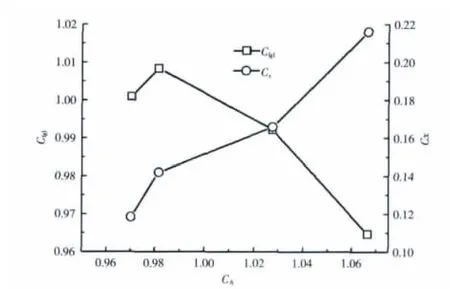
图10 不同CA下主流推力系数变化曲线

由于射流的屏蔽作用，主流从喷管出口到气动喉道这段距离不受大气影响。因此在气动喉道截面运用动量方程获得主流在射流影响下的实际推力，并且与无射流状况下主流实际推力作比较，得到主流推力系数Cfg1。同时，为了比较不同PRS下的气动喉道位置，设定系数CA为固体喉道面积与气体喉道面积之比，系数Cx为气体喉道远离出口距离与出口半径之比。

随着PRS的增大，气动喉道面积相应减小，CA逐渐增大，射流对出口气流进行再次压缩，主流推力系数先增大后减小。对于主流推力而言，气动喉道等同新的出口，而PRN小于设计值时，相应的最佳CA值增大，主流膨胀更充分，主流推力系数随之增大，且大于1，表示射流控制能有效提高主流推力。但随着PRS的增大，气动喉道面积减小，Cx增大，喉道位置远离出口，主流出口速度减小，整个喷管类似收敛喷管，主流推力系数随之减小。在PRN=2.135时，CA在0.97～0.99内能有效提高主流推力系数。

4 结论

（1）喷管出口注气改变了主流有效出口面积，使得有过膨胀损失的喷管被再次压缩膨胀，从而增大推力系数。在保证流量比小于0.1范围内，当PRN=2.135、PRS=1时，推力系数达到0.995，比无射流时的提高了1.7%，达到预期的固-气双喉道目的。

（2）射流角度对喷管出口实际面积和流场有一定影响；顺向射流能获得更好的推力效果。

（3）调节气动喉道面积能有效增大喷管主流推力系数，使喷管工作点向设计点靠拢，达到最优效果。

[1]Deere K A.Summary of fluidic thrust vectoring research conducted at NASA Lang-ley Research Center[R].AIAA-2003-3800.

[2]胡海洋，王强.跨声速条件下轴对称收扩喷管内外流场的数值研究[J].航空动力学报，2008，23（6）：1041-1045.

[3]Kowal H J.Advances in thrust vectoring and the application of flow-control technology[J].Canadian Aeronautics and Space Journal,2002,48（2）：145-151.

[4]Deere K A.Summary of fluidic thrust vectoring research conducted at NASA Langley Research Center[R].AIAA-2003-3800.

[5]Hamed A,Laskowski G.A parametric study of slot injectionthrust vectoring in a 2DCD nozzle[R].AIAA-97-3154,

[6]Yagle P J,Miller D N,Ginn K B,et al.Demonstration of fluidic throat skewing for thrust vectoring in structurally fixed nozzles[R].ASME 2000-GT-001.

[7]Flamm J D.Experimental study of a nozzle using fluidic counterflow for thrust vectoring[R].AIAA-98-3255.

[8]Deere K A,Berrier B L,Flamm J D.A computational study of a new dual throat fluidic thrust vectoring nozzle concept[R].AIAA-2005-3502.

[9]Flamm J D,Deere K A,Berrier B L,et al.Experimental study of a dual-throat fluidic thrust-vectoring nozzle concept[R].AIAA-2005-3503.

[10]Flamm J D,Deere K A,Mason M L,et al.Design enhancements of the two-dimensional dual throat fluidic thrust vectoring nozzle concept[R].AIAA-2006-3701.

[11]Flamm J D,Deere K A,Mason M L,et al.Experimental study of an axisymmetric dual throat fluidic thrust vectoring nozzle forsupersonic aircraftapplication[R].AIAA-2007-5085.

[12]Flamm J D.Experimental study of a nozzle using fluidic counterflow for thrust vectoring[R].AIAA-98-3255.

[13]PandaJ，SeasholtzRG.Velocityandtemperature measurement in supersonic free jets using spectrally resolved rayleigh scattering[R].AIAA-99-0296.

[14]额日其太，李喜喜，王强.轴对称喷管喉道面积射流控制数值模拟研究[J].推进技术，2010，31（3）：361-365.

[15]王庆伟，刘波，王如根.二元喷管气动喉道控制的数值模拟[J].航空学报，2009，30（2）：226-231.

[16]廉小纯，吴虎.航空燃气轮机原理[M].北京：国防工业出版社，2001：215-221.