安装误差对航空弧齿锥齿轮传动误差曲线的影响分析

刘光磊，张瑞庭，赵宁，江平

（1.西北工业大学机电学院，西安 710072；2.中航工业航空动力机械研究所，湖南 株洲 412002）

安装误差对航空弧齿锥齿轮传动误差曲线的影响分析

刘光磊1，张瑞庭1，赵宁1，江平2

（1.西北工业大学机电学院，西安 710072；2.中航工业航空动力机械研究所，湖南 株洲 412002）

刘光磊(1962)，男，博士，副教授，硕士生导师，主要研究方向为机械系统及其关键零部件工作能力分析与评价，以及弧齿锥齿轮设计与分析等。

传动误差曲线是评价弧齿锥齿轮副动态特性与啮合性能的重要指标，而安装误差又对动态特性与啮合性能产生直接影响。为此，分析了传动误差曲线对各类型安装误差变动的敏感性。依据局部综合法设计得到了齿轮副加工参数，形成弧齿锥齿轮副齿面。计入系统安装误差，通过对轮齿接触分析，得到了传动误差曲线与齿面接触印痕。定量分析了在不同安装误差条件下，传动误差曲线的变化情况，并对航空附件传动系统中的1对弧齿锥齿轮进行了传动误差曲线对安装误差的敏感性分析。结果表明：传动误差曲线对小轮安装距误差更为敏感。

弧齿锥齿轮；安装误差；轮齿接触分析；传动误差；敏感性分析

0 引言

弧齿锥齿轮因具有承载能力强、传动平稳、效率高等优点，被广泛地应用于航天、航空、航海、汽车和精密机床等机械传动领域。安装于实际传动系统中的弧齿锥齿轮，不可避免地存在系统安装误差。一定范围内的安装误差，可能不会对齿面接触印痕造成明显的影响；同时，在系统安装误差的影响下，传动误差曲线可能已经发生了一定程度的变化，该变化会对弧齿锥齿轮传动的平稳性、振动与噪声造成较大影响。因此，分析传动误差曲线对系统安装误差的敏感性，对于指导弧齿锥齿轮的安装调整，提高其动态啮合性能，降低振动与噪声，具有重要的理论与工程实际意义。

传动误差主要由弧齿锥齿轮的准共轭特性、变形及制造误差造成，对齿轮的动态特性有着重要的影响。其工作载荷时的曲线波动幅值决定了振动的大小，波动幅值越大，振动越大，噪声也越大[1-2]；Simon[3-4]通过分析不同安装误差值条件下，齿面接触印痕形状和位置的变化，研究了不同类型安装误差对准双曲面齿轮和弧齿锥齿轮啮合性能和传动误差的影响，但并没有比较在不同类型安装误差同等变动量的条件下传动误差的变化情况；刘光磊等[5]提出了航空弧齿锥齿轮低噪声和低安装误差敏感性设计方法，完成了某型航空弧齿锥齿轮的齿坯及加工参数设计，得到了对称型的传动误差曲线和接近于直线的啮合迹，但没有具体地分析安装误差对传动误差曲线的影响；张艳等[6]通过定量输入系统安装误差，分析了其对弧齿锥齿轮副齿面接触印痕变动的影响，但未对传动误差的变化进行分析；唐进元等[7]以加工误差与齿轮啮合性能的关系研究为重点，也研究了安装误差对啮合性能的影响，分析中采用的方法与传统的V-H分析方法无异，且没有对比不同类型安装误差对啮合性能的影响；吴训成等[8]研究了安装误差对齿面啮合点位置的影响，但没有涉及传动误差曲线。

本文依据局部综合法设计得到了弧齿锥齿轮加工参数，形成弧齿锥齿轮齿面；计入系统安装误差，通过轮齿接触分析，得到传动误差曲线和接触印痕；改变系统安装误差值的大小，对传动误差曲线幅值和接触印痕的变化进行比较，从而分析传动误差曲线对不同类型安装误差的敏感性，为高动态性能弧齿锥齿轮的实际安装调整提供理论分析与指导。

1 系统安装误差

根据国家标准GB11365-89[9]的规定，弧齿锥齿轮安装在实际装置上时，需要控制的安装误差项目主要包括齿圈轴向位移偏差ΔfAM、齿轮副轴间距偏差Δfa和交角偏差ΔE∑。其中，ΔfAM分别包括小轮、大轮安装距误差ΔH和ΔJ，如图1所示。从图中可见，以锥顶重合处为参考位置，规定安装误差向小端移动为负，向大端移动为正。Δfa用ΔV表示，规定以锥顶重合处为参考位置，从大轮正面看，小轮在大轮的右边，大轮向上移动为正，向下移动为负。ΔE∑用Δ∑表示，规定以锥顶重合处为参考位置，轴交角增大为正，轴交角减小为负。在该标准中，各项安装误差均以线长度计值。因此，轴交角偏差实际是由齿宽中点处的等量弧长偏差换算得到。

图1中其他符号的角标所代表的坐标系分别是：S1（O1;X1,Y1,Z1）和S2（O2;X2,Y2,Z2），分别表示与小轮、大轮固连的坐标系；Sd(Od;Xd,Yd,Zd)为固连于Sh（Oh,Xh,Yh,Zh）的辅助坐标系；Sh为啮合坐标系。

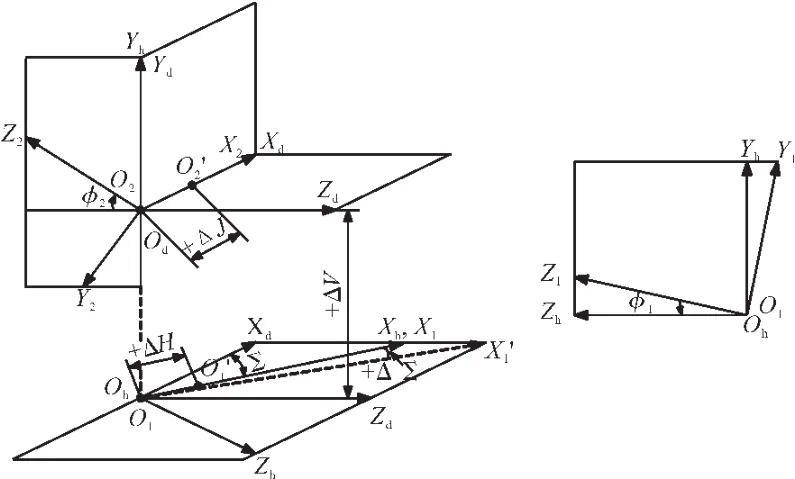
图1 计入系统安装误差的啮合坐标系

2 基于局部综合法的轮齿啮合分析

2.1 弧齿锥齿轮副齿面

局部综合法通过控制传动误差曲线的2阶导数和齿面在参考点处啮合时的接触状态，来控制齿面的啮合性能，并据此确定小轮和大轮的加工参数。

文献[10-11]根据配对齿面Σ（1）与Σ（2）之间的曲率关系，给出了局部综合法的基本方程组

式中：系数ai1、ai2、ai3的详细表达式见文献[10-11]；

由式（1）得到齿轮副的加工参数，将刀具齿面经过一系列坐标变换，即可形成齿轮的齿面。

2.2 含安装误差的轮齿啮合分析

获取弧齿锥齿轮的齿面后，通过式（2）将小、大轮的齿面和法线方程分别转换到啮合固定坐标系中

式中：θp、φcr1为展成小轮齿面时的曲面坐标；θg、φcr2为展成大轮齿面时的曲面坐标；Mh1、Md2、Mhd为含安装误差的坐标变换矩阵；M′h1、M′d2、M′hd为自由矢量变换矩阵，分别由Mh1、Md2、M′hd去掉最后1行1列得到；矢量r、n为齿面上任意点处的径矢和法矢；角标表示所在的坐标系。

当弧齿锥齿轮副啮合时，2个齿轮的齿面从啮入到啮出始终连续相切，故在啮合坐标系Sh中，有如下的TCA基本方程组[10]

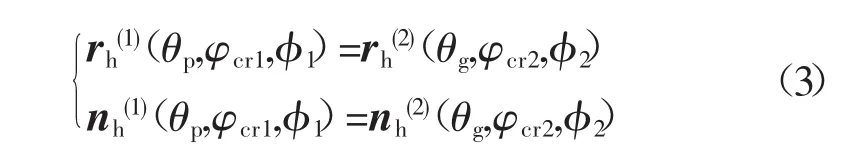
式中：φ1、φ2分别为小轮和大轮在啮合时的转角。

在ΔH、ΔJ、ΔV、Δ∑取值不同的条件下，求解式（3），可以得到含安装误差时弧齿锥齿轮副的传动误差曲线与齿面接触印痕。

3 传动误差曲线

传动误差曲线是评价弧齿锥齿轮啮合性能的重要指标。理想的传动误差曲线为1条中凸的对称型抛物线，并且相邻齿对所形成的各曲线相交。该设计可以使得从动轮在转动过程中经历1个由慢到快的啮入和由快到慢的啮出过程，并且啮入加速和啮出减速的程度基本一致，使齿轮的啮合过程尽可能平稳、安静，并有利于减少齿轮安装误差对啮合性能的影响，如图2所示。从图中可见，预置的传动误差曲线为对称的抛物线，横坐标为小轮在啮合时的转角，纵坐标为大轮在啮合时的转角与理论转角之差，A和A′为相邻传动误差曲线的交点，B和C分别为传动误差曲线的起点和终点。

图2 传动误差曲线及其交点

传动误差函数Δφ2[1,10]按下式计算

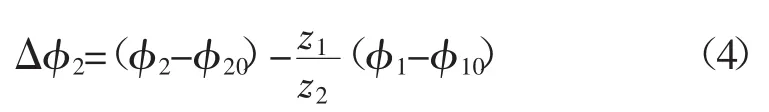
式中：φ10、φ20分别为小轮和大轮从加工起始位置算起，到二者在参考点M处啮合时各自需要转过的角度；z1、z2为2个齿轮的齿数。

A和A′的纵坐标即为传动误差曲线的幅值。在各单因素安装误差同等变动量的条件下，经TCA分析，得到不同类型安装误差时的传动误差曲线幅值，与无误差时的进行比较后，可以定量地评价传动误差曲线对不同类型安装误差的敏感性。

4 数值算例

利用某型航空发动机附件传动系统中的1对弧齿锥齿轮，以“小轮凹面、大轮凸面”的情况为例，进行传动误差曲线对安装误差的敏感性分析。轮坯几何参数见表1，大轮加工参数见表2，局部综合参数见表3，小轮凹面加工参数见表4。

在无安装误差和安装误差各自取0.003 mm时，经TCA得到的传动误差曲线和齿面接触印痕分别如图3～7所示。安装误差取值按GB/T11365-89中规定的5级精度齿轮所允许的安装极限偏差值而定。各项安装误差在± 0.005 mm范围内，单独变化时的传动误差曲线幅值变动如图8所示。

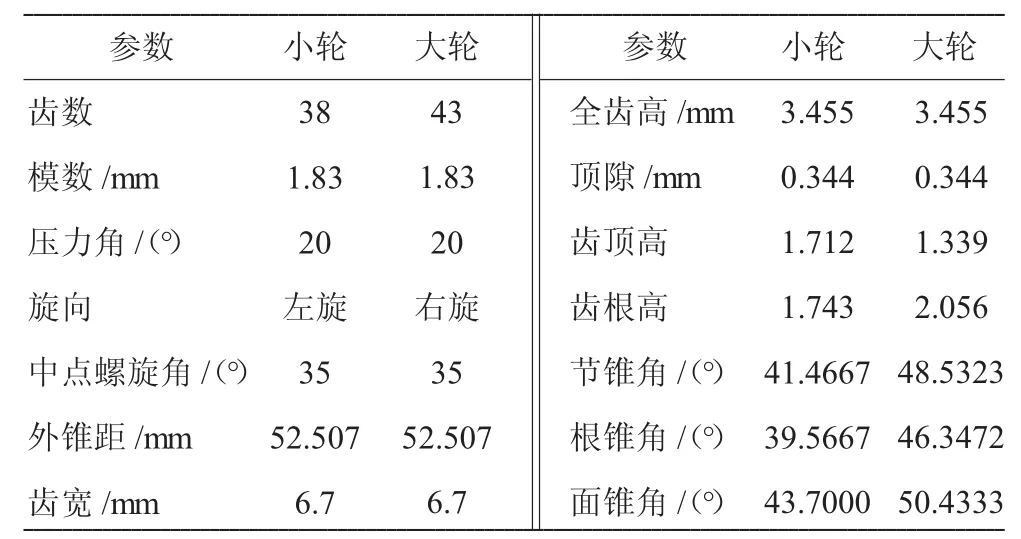
表1 轮坯几何参数

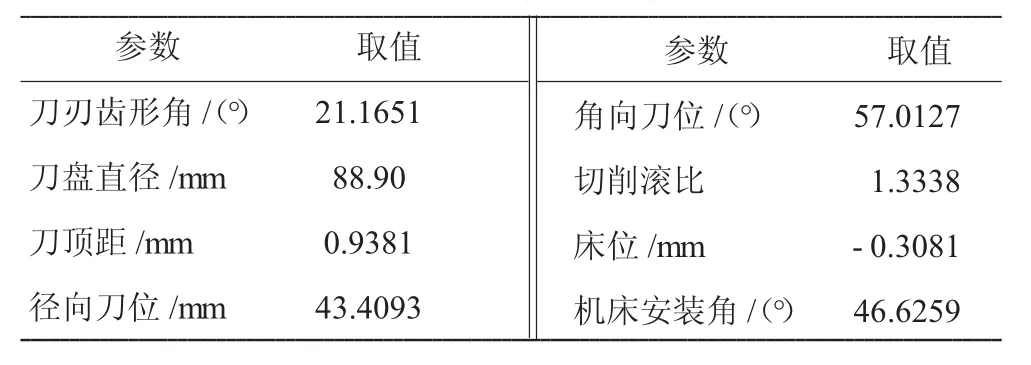
表2 大轮加工参数

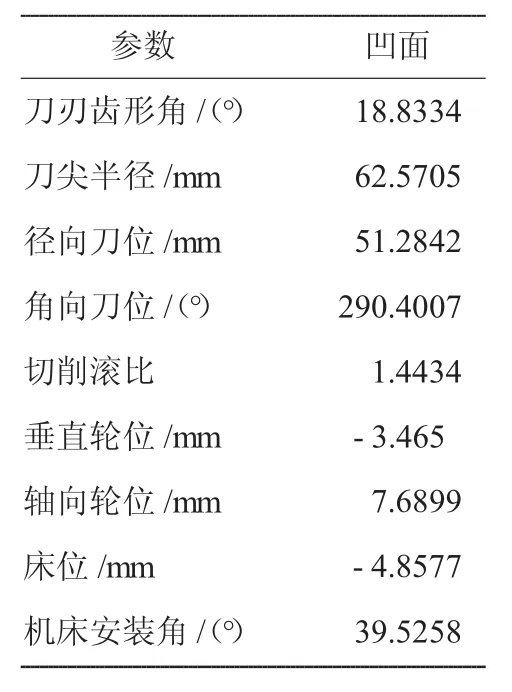
表4 小轮凹面加工参数

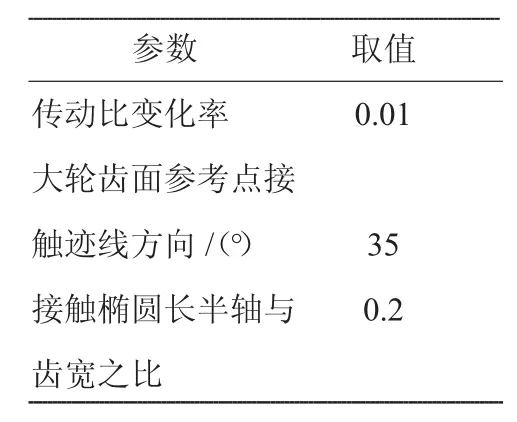
表3 局部综合参数

从图8中传动误差曲线幅值相对变动量的情况可见，传动误差曲线对小轮安装距误差最为敏感，所以在实际弧齿锥齿轮的安装调整中要严格控制小轮的安装距误差。对其余安装误差的敏感性由强到弱的顺序为大轮安装距误差、轴交角误差和偏置距误差。因弧齿锥齿轮齿面无法用数学表达式描述，所以本文的结论未必能够适用于所有的弧齿锥齿轮。但采用本文方法所开发的软件，可以分析具体弧齿锥齿轮传动误差曲线对安装误差变动的敏感性，从而为工程实际提供参考。

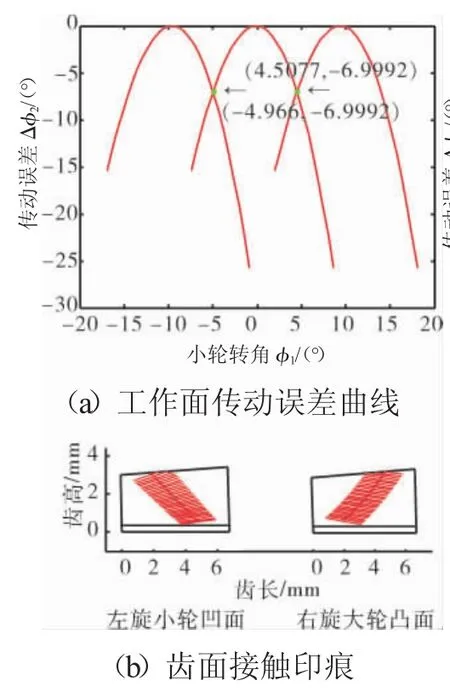
图5 ΔJ=0.003 mm时的传动误差曲线和齿面接触印痕

图6 ΔV=0.003 mm时的传动误差曲线和齿面接触印痕

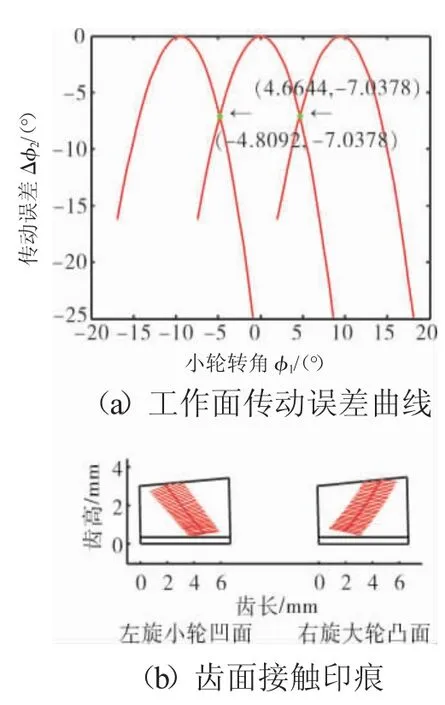
图7 Δ∑=0.0035°时的传动误差曲线和齿面接触印痕

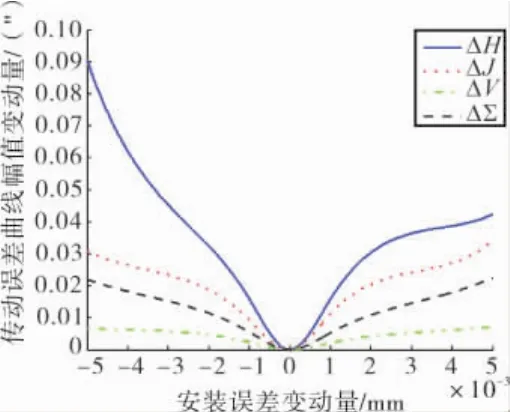
图8 安装误差在±0.005 mm内的传动误差曲线幅值变化

5 结束语

本文提出了航空弧齿锥齿轮传动误差曲线对安装误差的敏感性分析的思路和方法。以某型航空发动机附件传动系统中的1对弧齿锥齿轮副为例，进行了传动误差曲线对安装误差的敏感性分析。结果表明：传动误差曲线对小轮安装距误差最为敏感，对大轮安装距误差、轴交角误差和偏置距误差的敏感性由强到弱。

采用本文提出的方法及开发的软件，可以得到安装误差与弧齿锥齿轮传动误差曲线之间的定量关系，为预判各项安装误差对弧齿锥齿轮的振动和噪声的影响程度提供参考。

[1]方宗德，刘涛，邓效忠.基于传动误差设计的弧齿锥齿轮啮合分析[J].航空学报，2002，23（3）：226-230.

[2]曹雪梅，周彦伟，邓效忠，等.弧齿锥齿轮的传动误差、重合度和噪声的关系[J].机械传动，2003，27（2）：43-45.

[3]Vilmos S.The influence of misalignments on mesh performances ofhypoid gears[J].Mechanism and Machine Theory，1998，33：1277-1291.

[4]Vilmos S.Influence of tooth errors and misalignments on tooth contact in spiral bevel gears[J].Mechanism and Machine Theory，2008，43：1253-1267.

[5]刘光磊，樊红卫，谷霁红，等.航空弧齿锥齿轮低噪声低安装误差敏感性设计[J].航空发动机，2010，36（2）：43-45.

[6]张艳，黄乾贵.安装误差对正交弧齿锥齿轮副接触区影响的分析[J].阜新矿业学院学报，1992，11（4）：79-84.

[7]唐进元，卢延峰，周超.有误差的螺旋锥齿轮传动接触分析[J].2008，44（7）：16-23.

[8]吴训成，毛世民，吴序堂.点接触齿面的安装误差敏感性研究[J].2000，11（6）：700-703.

[9]徐灏.机械设计手册：第4卷[S].2版.北京：机械工业出版社，2000：183-197.

[10]Litvin F L，Zhang Yi.Local synthesis and tooth contact analysisofface-milledspiralbevelgears[R]．NASA-TR-90-C-028.

[11]Litvin F L.Gear geometry and applied theory[M].New Jersey：PTR Prentice Hall，1994：233-240.

Effect of Installation Error on Transmission Error Curve for Aero Spiral Bevel Gears

LIU Guang-lei1,ZHANG Rui-ting1,ZHAO Ning1,JIANG Ping2
（1.School of Mechatronic Engineering,Northwestern Polytechnical University,Xi'an

710072,China；2.AVIC Aviation Powerplant Research Institute,Zhuzhou Hunan 412002,China）

Transmission error curve was an important index for evaluating the dynamic characteristics and meshing performance which were influenced by installation errors instinctively.The sensitivity of transmission error curve to different types of installation errors was analyzed.Manufacture parameters were designed according to local synthesis,and the tooth surfaces of spiral bevel gears were formed.Transmission error curves and tooth contact patterns were obtained by tooth contact analysis(TCA)under installation errors. Variation and sensitivity of transmission error curve to installation errors were analyzed quantitatively under different installation error conditions.A pair of spiral bevel gear on aero accessory drive system was used for analyzing the sensitivity of transmission error curve to installationerrors.Theresultsshowthattransmissionerrorcurveismoresensitivetopinionaxisinstallationerror.

spiral bevel gears;installation error;tooth contact analysis(TCA);transmission errors;sensitivity analysis

2011-10-20