球面收敛调节片喷管RCS数值模拟研究

崔金辉，杨青真，陈立海

（西北工业大学动力与能源学院，西安 710072）

球面收敛调节片喷管RCS数值模拟研究

崔金辉，杨青真，陈立海

（西北工业大学动力与能源学院，西安 710072）

崔金辉（1987），男，在读硕士研究生，研究方向为航空发动机总体设计。

结合物理光学迭代法（IPO）和等效棱边电磁流法（EEC），自主开发了电大尺寸腔体电磁散射特性计算程序，并通过对某试验模型雷达散射截面积（RCS）进行计算，完成了程序的可靠性验证。利用该程序对带有电磁信号遮挡板且采用3种不同尾缘修形技术的球面收敛调节片矢量喷管（SCFN）进行了RCS数值模拟研究。结果表明：随着入射方位角的增大，喷管的RCS整体上有减小的趋势；喷管尾缘的修形只有在雷达波以较大方位角入射时对减小RCS效果明显；电磁信号遮挡板的存在很大程度上减弱了喷管的电磁信号特征。

球面收敛调节片矢量喷管；修形技术；雷达散射截面积；物理光学迭代法；等效棱边电磁流法；航空发动机

0 引言

作为大尺寸复杂腔体结构的典型代表，航空发动机尾喷管是飞行器的强散射回波源之一，对飞行器整机雷达散射截面发挥着重要作用。因此，开展尾喷管电磁抑制措施的研究对改善飞行器总体的电磁隐身性能具有重要意义。对喷管出口进行适当的修形可以减弱雷达绕射回波，降低雷达散射截面积，提高喷管的电磁隐身性能[1]。球面收敛调节片矢量喷管是1种多功能2元矢量喷管，可以提供俯仰、偏航、反向等全方位的矢量推力，并且目标特征信号低，有很好的隐身特性，是惟一列入综合高性能涡轮发动机技术（IHPTET）计划的多功能推力矢量喷管[2-7]。目前，国内外对该喷管技术的研究也仅仅局限在气动和红外隐身方面[8-12]，有关电磁隐身技术研究方面的文献还很少见。

本文通过对采用3种不同喷口尾缘修形技术来抑制电磁散射强度的喷管模型，进行电磁散射特性数值模拟研究，并对采用不同修形技术的电磁抑制效果进行了对比分析。

1 物理模型

3种SCFN喷管分为3段，即进口过渡段、球面收敛段和矩形扩张段。其中，进口过渡段和球面收敛段的尺寸与形状完全一致，而对矩形扩张段尾缘采用不同的修形技术[13]，喷管的3维外形如图1所示。图中标明了入射临界角的大小，入射临界角即电磁波能够入射到喷管内部的最大方位角。基本模型将下侧扩张调节片的直边尾缘以平行于喷管轴线的方向向下游延伸762 mm形成遮挡板，斜切口模型是在基本模型的基础上将出口尾缘做30°斜切，锯齿形模型也是在基本模型的基础上将出口尾缘向两侧分别做45°斜切，其他几何参数见表1。

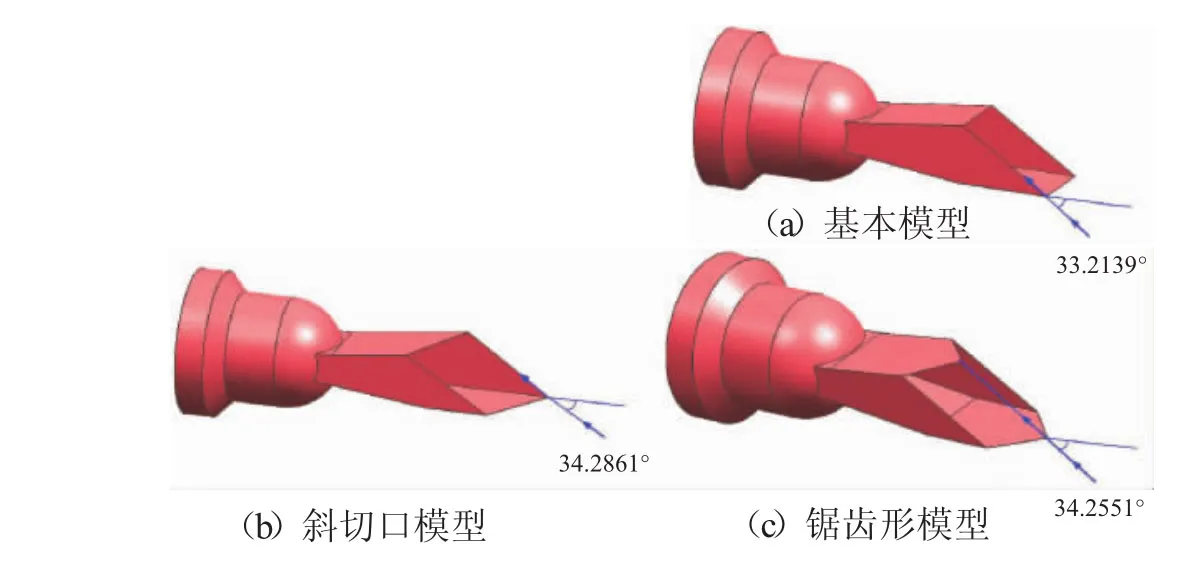
图13 种喷管的3维外形

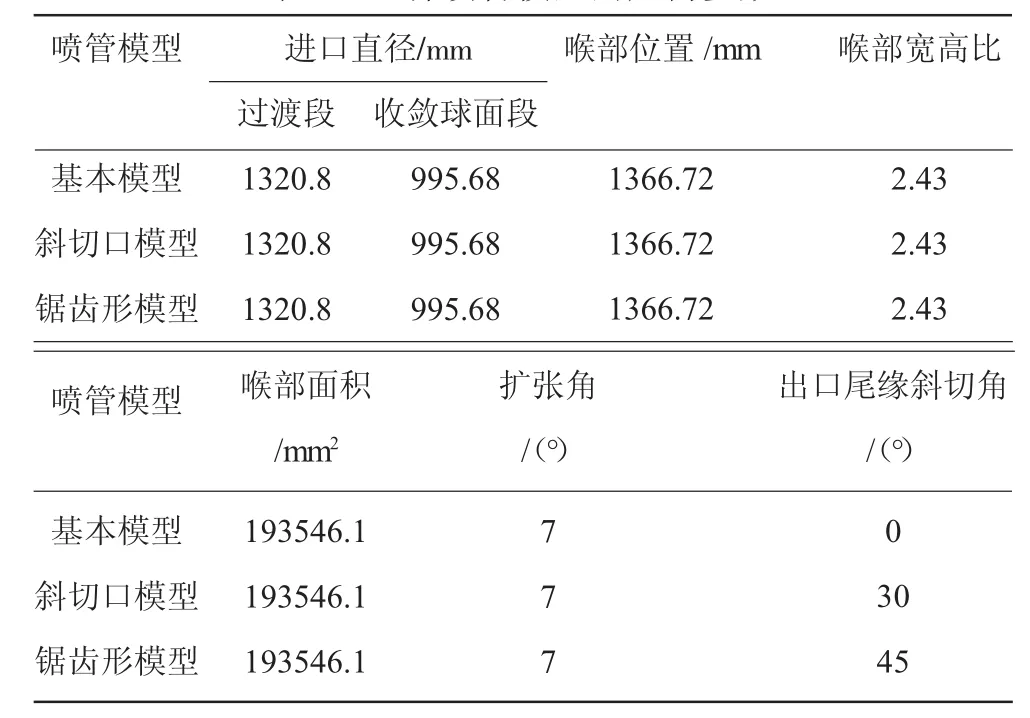
表13 种喷管模型的几何参数

2 计算方法

2.1 物理光学迭代法

F.Obelleiro等人提出的物理光学迭代（IPO）方法是分析电大尺寸腔体散射特性的1种行之有效的高频近似方法[14-15]，是在物理光学电流的基础上考虑多次散射的1种迭代方法，用光学电流与修正电流叠加来逼近导体目标表面的实际电流，进而求解其电磁散射。

由于目标和雷达之间的距离很远，因此入射电磁波可以当作平面波处理。电磁波入射到单端开口腔体中，如图2所示。在图中，Es和Ei分别为散射电场矢量和入射电场矢量初始电流J0（rc）可以通过物理光学法得到

式中：J（0r）c为初始电流矢量；n为指向腔内的法向单位矢量；rc为腔体内壁面Sc上任一点的位置矢量；表示入射磁场矢量。

图2 开口腔体

腔体内壁面上的真实电流Jn（rc）可以通过磁场积分方程（MFIE）的迭代求解得到

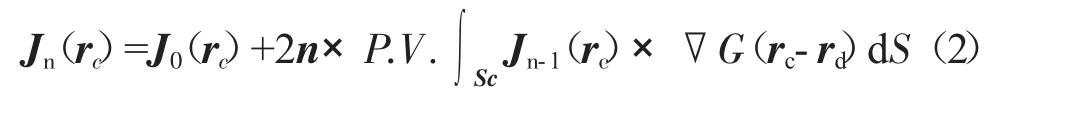
式中：Jn（rc）为真实电流矢量；下标n为迭代次数；P.V.为内壁面Sc区域内的主值积分；▽G为自由空间格林函数的梯度。

基于面元之间的照射关系，可以通过以上方程的迭代计算模拟电磁波的多次反射。

为了加快计算的迭代收敛速度，在IPO方法迭代过程中采用前后向算法，并引入欠松弛因子w（0＜w≤1）[15]。根据经验，一般不太复杂的腔体取w=0.8～0.9，较复杂的腔体取w=0.6～0.7[16]，在本文取w=0.8。

2.2 等效棱边电磁流法

等效棱边电磁流法(EEC)[17-18]是求解边缘绕射比较有效和常用的方法，可以较为准确地计算喷管出口棱边绕射场RCS值，采用EEC可以计算单站任意方向上的绕射场而不会出现奇异性。EEC是假设在环绕表面奇异性(边缘回路)的各点处存在线电流矢量I和线磁流矢量M，当以远场辐射积分的形式对其求和来表示绕射场时，得到1个有限的结果。

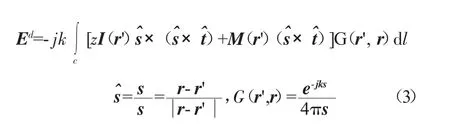
式中：Ed表示绕射电场矢量；j为虚数单位；k为入射电磁波的波数；z为媒质的阻抗；r'，r分别为观察点和边缘C上任一点的位置矢量；dl为沿着边缘C的弧长l的增量为沿着C的单位矢量，s分别为从边缘C上某点到观察点之间的单位矢量和距离；G（r',r）为3维格林函数；I（r'）=I（r'），M（r'）=M（r'）分别为等效电磁流矢量和磁流矢量。I（r'）和M（r'）分别为r'处的电流和磁流的大小；上标k为自由空间波矢。

在用EEC求解边缘绕射场时，等效电磁流I（r'）、M（r'）的计算就可近似转化为对2维尖劈渐近端点的计算，如图3所示。

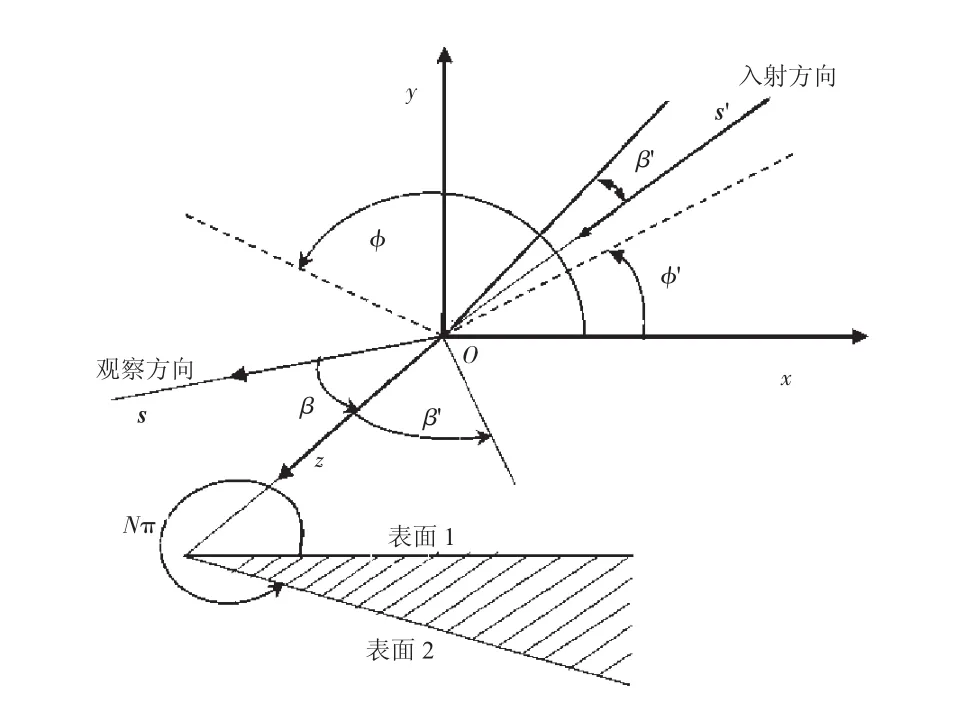
图3 尖劈散射

在图3中：虚线是入射方向和观察方向在xOy平面内的投影；O为原点；x轴垂直于边缘并位于上侧劈面上；y轴为劈面的外法向；z轴沿着边缘并切于点O，形成右手坐标系ˆ和分别为观察方向和入射方向矢量；边缘C和ˆ'之间的夹角分别为β和β'；上劈面与'和所决定的入射平面之间的夹角为φ'；上劈面与和所决定的平面之间的夹角为φ；在线电流I和线磁流M中，对后续计算有用的是边缘绕射场的分量If和Mf[19]。

3 程序可靠性验证

为了验证程序的可靠性，对文献[20]中提供的单端开口圆柱腔体模型进行了RCS数值模拟计算。圆柱腔体沿x轴放置，沿正x方向开口。计算时采用的入射波频率f=10 GHz，即波长λ=0.03 m，腔体长度L=10λ，直径D=6λ。水平极化和垂直极化方式下计算值与文献参考值对比如图4、5所示，RCS（θθ）和RCS（φφ）分别表示2种极化时的数值模拟结果。纵坐标中的RCS（θθ）和RCS（φφ）分别表示水平极化方向的垂直极化方向的RCS值，分贝（dB）为RCS的单位，横坐标θ（°）表示入射方位角的大小。

利用本文程序计算所得到的结果（图4、5）与文献[20]中提供的数据非常吻合，因此，文中使用的程序有较高的可靠性和计算精度。

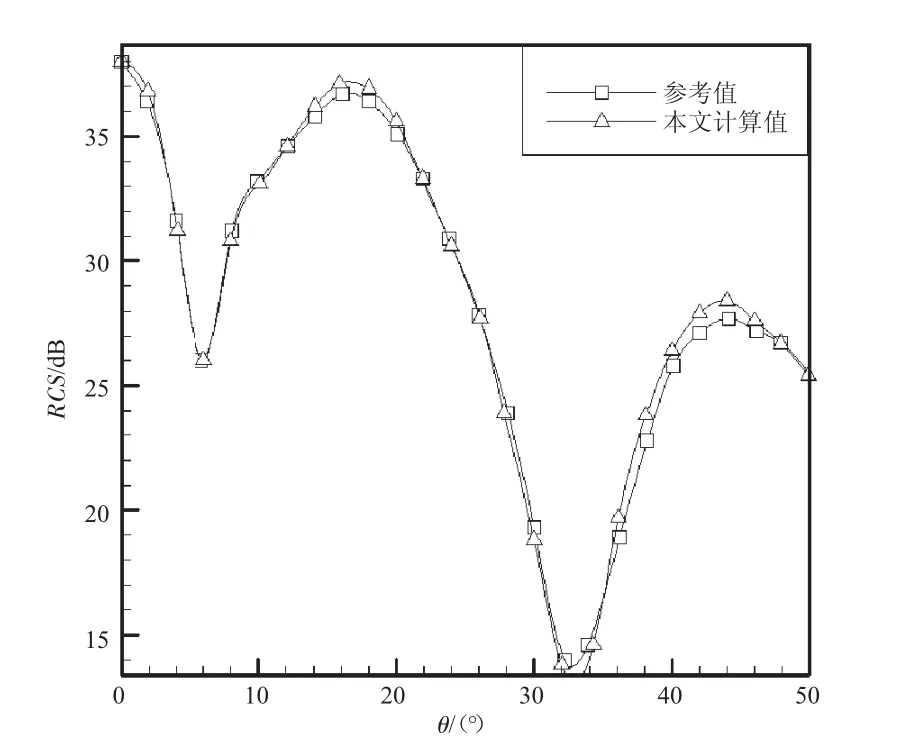
图4 水平极化时结果对比

图5 垂直极化时结果对比

4 计算结果与分析

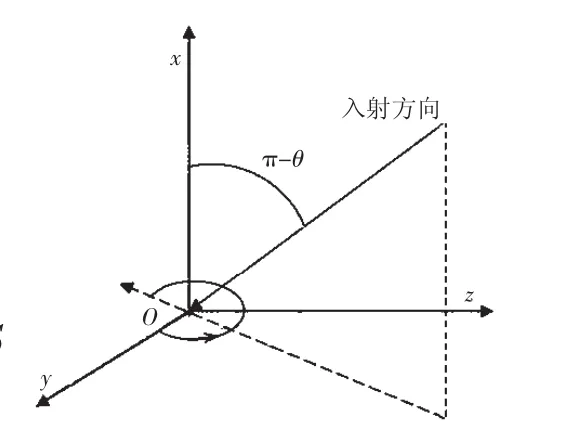
图6 入射方向定义

本文结合IPO法和EEC法，对基本模型、斜切口模型和锯齿形模型等3种喷管模型分别进行RCS数值模拟计算，入射方向的定义如图6所示。

在图中，θ为入射方向和x轴正向的夹角，φ为y轴正向到入射方向在yOz面上的投影之间的夹角。喷管沿x轴正向放置，θ=0°～40°，φ=0°。

水平和垂直极化方式下基本模型、斜切口模型和锯齿形模型3种喷管的RCS随入射方位角的变化如图7、8所示。

从图7、8中可见：

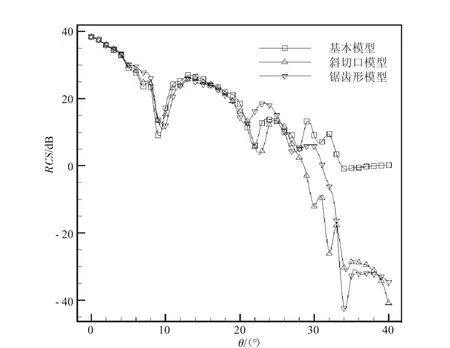
图7 水平极化下的RCS分布曲线

图8 垂直极化下的RCS分布曲线

（1）在所计算的角度范围内，随着入射方位角θ的增大，3种喷管的RCS整体上都有减小的趋势，其中，θ=0°时，RCS值同时达到最大。这是因为，本文在建模时，将喷管的进口端简化为1个平面，从喷管后方以0°入射到喷管内部的电磁波与喷管进口平面正好呈90°，即垂直照射在喷管进口端平面上，大部分波会直接反射回去，形成了很强的回波源，因此感应电流很大，导致在0°方向上RCS值达到最大。

（2）3种喷管的RCS值在0°方向上达到最大的同时，其最大值也基本相等。在水平极化时，喷管在0°方向上的RCS都约为38.3 dB；在垂直极化时，RCS都约为32.0 dB。这是因为，喷管的喉部面积相同，导致了能够从0°方向入射到进口端的电磁波数量也基本相同（虽然喷管的扩张壁面以及遮挡板也会反射一部分波，但是相对较少），因此，产生的感应电流大小也基本相等，所以在0°方向的RCS值基本相同。

（3）在水平极化方位角为0°～28°，和在垂直极化方位角为0°～26°时，3种喷管的RCS值基本相等，只是在某些角度上有很小的差别。这就说明对喷管尾缘的修形在此角度范围内起不到降低RCS的作用。而在水平极化方位角为28°～40°和垂直极化方位角为26°～40°时，3种喷管的RCS则出现明显分化，斜切口模型和锯齿形喷管的RCS明显减小，基本模型的RCS逐渐大于其他2种喷管的，并且随着入射角的增大，其差值也越来越大。说明对喷管尾缘的修形在此角度范围内起到了降低RCS的作用。因此，从上述分析可知，对喷管尾缘所做的斜切口以及锯齿形等修形方式在雷达波以大角度入射时对减小RCS效果明显，而在雷达波以小角度入射时效果则不明显。

（4）在方位角较大（如基本模型的θ≥34°和斜切口模型与锯齿形模型的θ≥35°）时，3种喷管的RCS曲线突然变得较为平缓，其中，基本模型表现得尤为明显。这是因为遮挡板的存在使得以较大方位角入射的电磁波照射不到喷管腔体的内部，基本、斜切口和锯齿形模型的入射临界角分别为33.2139°、34.2861°和34.2551°，如果入射方位角超过入射临界角，则入射电磁波就不能射入喷管腔体的内部，因此，喷管的RCS完全取决于各自喷管所带遮挡板的边缘绕射场的RCS，边缘绕射场的RCS主要取决于各自尾缘形状，由于喷管各自的遮挡板尾缘形状是固定不变的，因此在此角度范围内的RCS曲线各自保持平缓变化，变化梯度较小。但是，由于3种喷管各自遮挡板的出口边缘修形不同，导致了其边缘绕射场的RCS明显不同，基本模型喷管的RCS要明显大于其他2种喷管的，即修形后的喷管比未修形的喷管有着更好的电磁隐身性能。进一步说明对喷管出口尾缘的修形起到了降低RCS的作用，同时也解释了关于修形在电磁波以较大方位角入射时能够减小RCS的原因。

5 结论

（1）本文结合物理光学迭代法和等效棱边电磁流法开发的电磁散射特性计算程序具有较高的精度和可靠性。

（2）随着入射方位角的增大，3种喷管的RCS整体上都有减小的趋势。入射方位角为0°时，3种喷管的RCS值同时达到最大，其最大值也基本相等。

（3）对喷管尾缘采用的斜切口及锯齿形等修形方式，只有在雷达波以较大方位角入射时对减小RCS效果明显，在小角度入射时效果不明显。

（4）电磁信号遮挡板可以阻挡以较大方位角入射的电磁波，在很大程度上减弱了喷管的电磁信号特征。参考文献：

[1]Arnon S,Rotman S R,Kopeika N S.Bandwidth maximization for satellite laser communication[J].IEEE Trans.on Aerospace and Electronic Systems,1999,35（2）：675-682.

[2]梁春华，靳宝林，李雨桐.球面收敛调节片推力矢量喷管的发展[J].航空发动机，2002（3）：55-58.

[3]方昌德.航空发动机的发展前景[J].航空发动机，2004，30（1）：1-5.

[4]Berrier B L,Taylor J G.Internal performance of two nozzles utilizing gimbal concepts for thrust vectoring[R].NASATP-2991.

[5]TaylorJG.Internalperformanceofahybrid axisymmetric/nonaxisymmetric convergent-divergent nozzle[R]. NASA-TM-4230.

[6]Wing David J.Static thrust and vectoring performance of a sphericalconvergentflapnozzlewithanonrectangular divergent duct[R].NASA-TP-1998-206912.

[7]赵景芸，金捷.推力矢量技术的研究与发展[J].燃气涡轮试验与研究，1999，12（1）：51-54.

[8]王宏亮，张靖周，单勇.球形收敛调节片喷管静态内性能数值研究[J].推进技术，2008，29（4）：443-447.

[9]张靖周，谢志荣，郑礼宝.球面收敛二元扩张矢量喷管热射流特征的实验研究[J].燃气涡轮试验与研究，2004，17（3）：6-9.

[10]宋洁，王强.复杂形式球型收敛调节片喷管内流场计算及分析[J].航空动力学报，2007，22（8）：1325-1329.

[11]赵一鄂，余少志.复杂几何形状喷管内外三维流场的数值模拟[J].推进技术，2000，21（3）：30-33.

[12]王宏亮，张靖周，单勇.球型收敛调节片喷管红外特性数值研究[J].航空学报，2009，30（9）：1576-1582.

[13]Milton L,Taylor J G,Mark C F.Static internal performance of a two-dimensional convergent-divergent nozzle with external shelf[R].NASA-TM-4719.

[14]Fernando O B,Jose L R,Burkholder R J.An iterative physical optics approach for analyzing the electromagnetic scattering by large open-ended cavities[J].IEEE Transaction Antennas Propagat,1995,43（4）：356-361.

[15]Burkholder R J,Tomas L.Forward-backward iterative physicalopticsalgorithmforcomputingtheRCSof open-ended cavities[J].IEEE Transaction Antennas Propagat, 2005,53（5）：793-799.

[16]闫玉波，葛德彪，聂小春，等.应用改进迭代物理光学方法分析电大尺寸开口腔体散射[J].微波学报，2001，17（1）：35-39.

[17]Michaeli A.Elimination of infinities in equivalent edge currents,Part I：Fringe current components[J].IEEE TransactiononAntennasPropagation,1986,34（7）：912-918.

[18]Michaeli A.Equivalent edge currents for arbitrary aspects of observation[J].IEEETransactiononAntennasand Propagation,1984,32（3）：252-258.

[19]杨涛.飞行器动力系统腔体RCS数值模拟研究[D].西安：西北工业大学，2011.

[20]顾长青，舒永泽，徐金平.物理光学迭代法的子域连接法[J].电子学报，2001，29（3）：420-422.

Numerical Simulation of RCS for Spherical Convergent Flap Nozzle

CUI Jin-hui,YANG Qing-zhen,CHEN Li-hai
（School of Power and Energy,Northwestern Polytechnical University,Xi'an 710072,China）

Combining Iterative Physical Optic(IPO)and Equivalent Edge Currents (EEC),a code for calculating the electromagnetic scattering characteristics of electrically large cavities was developed.The reliability of the code was validated through calculating Radar Cross Section(RCS)of an experiment model. Based on the code,RCS of Spherical Convergent Flap Nozzles(SCFN)with the electromagnetic signal shade and three different trailing edges shaping techniques was simulated.The results show that the RCS of the three nozzles has a decreasing tendency on the whole with the increase of the azimuth angles.The effect of trailing edges shaping technique on RCS is obvious only when the electromagnetic wave incidents at large azimuth angles.The electromagnetic signature characteristics of the nozzle is weaken largely by the external shelf weakens.

Spherical Convergent Flap Nozzle;shaping technique;Radar Cross Section;Iterative Physical Optic;Equivalent Edge Currents;aeroengine

2011-10-17