(h-m)-凸函数的一些不等式

黄 洁，徐 璇，张宇槐，杨 瑜

(浙江外国语学院科学技术学院，浙江杭州310012)

(h-m)-凸函数的一些不等式

黄 洁，徐 璇，张宇槐，杨 瑜*

(浙江外国语学院科学技术学院，浙江杭州310012)

研究了(h-m)-凸函数的一些不等式，利用分析的方法，获得了(h-m)-凸函数不等式的4个结论，推广了相应文献中的结果.

(h-m)-凸函数;不等式;超相乘函数

1 引言

凸函数在各种不等式中起着重要的作用，近年来引起了不少学者的关注，参见文献［1-3］.最近，文献［4］给出了h-凸函数的定义并研究了h-凸函数的一些性质和不等式.文献［5］在文献［4］的基础上，进一步研究了h-凸函数的一些不等式.而文献［6］给出了(h-m)-凸函数的定义.受文献［4-6］的启发，本文研究(h-m)-凸函数的一些不等式，推广了文献［4］和［5］的相应结果.

2 预备知识

令I和J是R上的区间，为证明本文的主要结果，我们需要如下的一些定义和引理，定义1-3参见文献［4-6］.

定义1 设函数h:J→R是非负的且h≠0，f:I→R是非负的且对任意的x，y∈I和α∈(0，1)，都有

则称f:I→R是h-凸函数.反之，称f:I→R是h-凹函数.

定义2 函数h:J⊆R→R是非负的.当f为非负且对任意的x，y∈ 0，[ ]b(b＞0)，m∈ 0，[ ]1和α∈(0，1)，都有

则称f:［0，b］→R是(h-m)-凸函数.反之，称f:［0，b］→R是(h-m)-凹函数.

定义3 函数h:J→R，若对任意的x，y∈J，有h(xy)≥h(x)h(y)成立，则称h:J→R是超相乘函数.反之，称h:J→R是非超相乘函数.

引理1 假设h:J→R是非负的超相乘函数，f:I→R是(h-m)-凸函数且m∈(0，1］，令x1，x2，x3∈I且x1＜x2＜x3，则

当h是非负的非超相乘函数且满足f:I→R是(h-m)-凹函数时，不等号反向.

证明 f是(h-m)-凸函数，令x1，x2，x3∈I且x1＜x2＜x3，则

又因为h为非负的超相乘函数，故

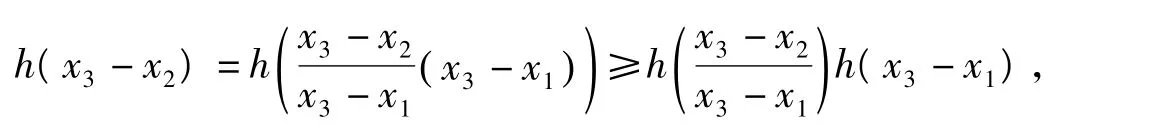
同理得

令h(x3-x1)＞0，由于f为(h-m)-凸函数，不妨令(1)式中的

则

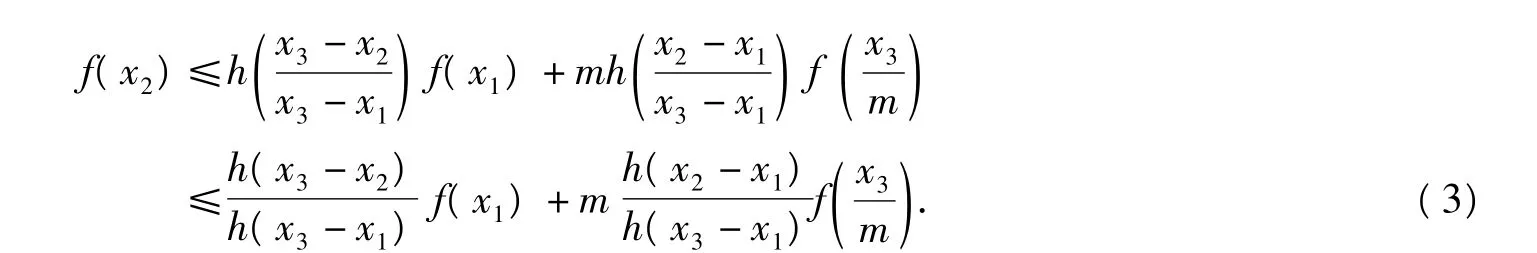
故(1)式化为两边同乘以h(x3-x1)即得(2)式.

3 主要结果和证明

下面，我们给出本文的主要结果.

定理1 ω1，…，ωn是正实数(n≥2)，当h是非负的超相乘函数且满足f是(h-m)-凸函数，m∈ [0 ，1]，x1，…，xn∈I，则

证明 因为f是(h-m)-凸函数，当n=2时，有

故(4)式成立.

假设当n=k-1时，(4)式成立，即

因此，当n=k时，

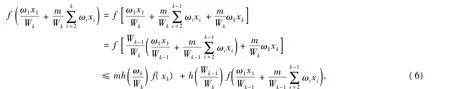
将(5)式代入(6)式得

又因为h是非负的超相乘函数，所以由定义3知(7)式可化为

故当n=k时，(4)式成立.

定理得证.

注1 当m=1，即f是h-凸函数，定理1即文献［4］中的定理19.

推论1 当h是非负的超相乘函数且满足f是(h-m)-凸函数时，x1，…，xn∈I，m∈［0，1］，则

定理2 假设w1，…，wn是正实数，(m0，M)⊆I，h:(0，∞)→R为非负的超相乘函数，并且f是(hm)-凸函数，对于任意的x1，…，xn∈(m0，M)，m∈(0，1］，则

当h是非负的非超相乘函数且f是(h-m)-凹函数时，不等号反向.

证明 根据引理1，在式(3)中取x3=M，x2=xi和x1=m0得

注2 当m=1时，即f是h-凸函数，定理2即为文献［4］中的定理21.

定理3 设h:J⊆R→R是非负的超相乘函数，若对于任意的x1，x2，…，xn∈［0，b］(b＞0)，m∈(0，1］，f:［0，b］→R是(h-m)-凸函数，则

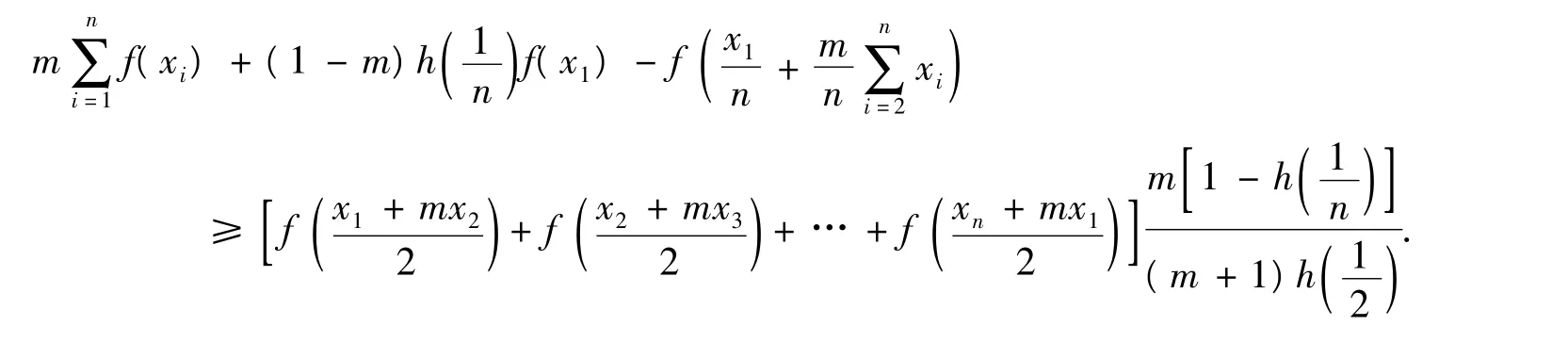
证明 因为f:［0，b］→R是(h-m)-凸函数，则

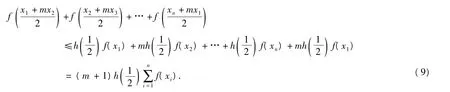
而

由推论1知，(10)式可化为

将(11)式代入(9)式得

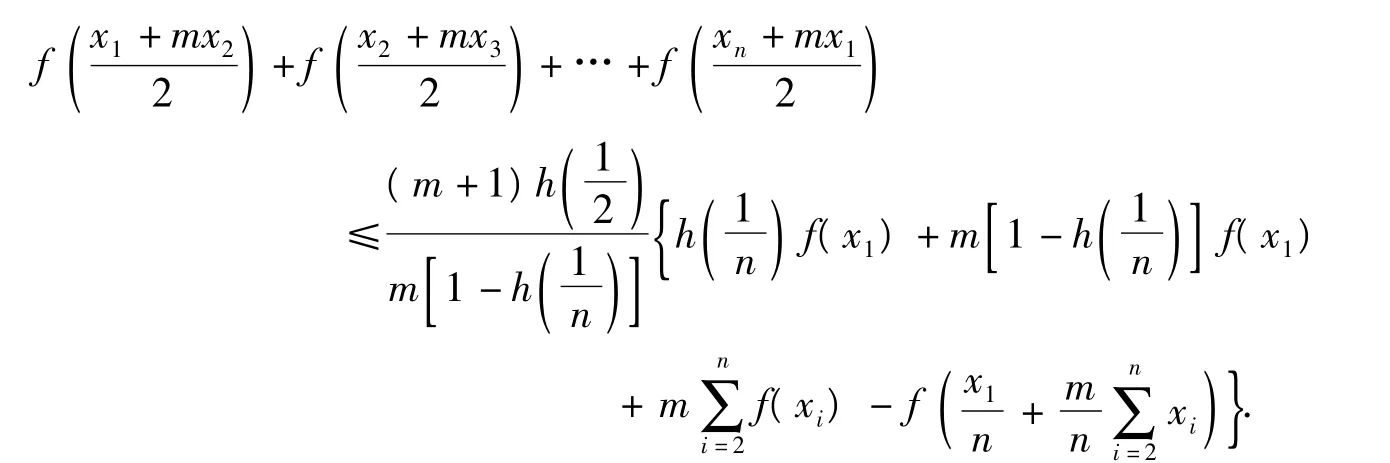
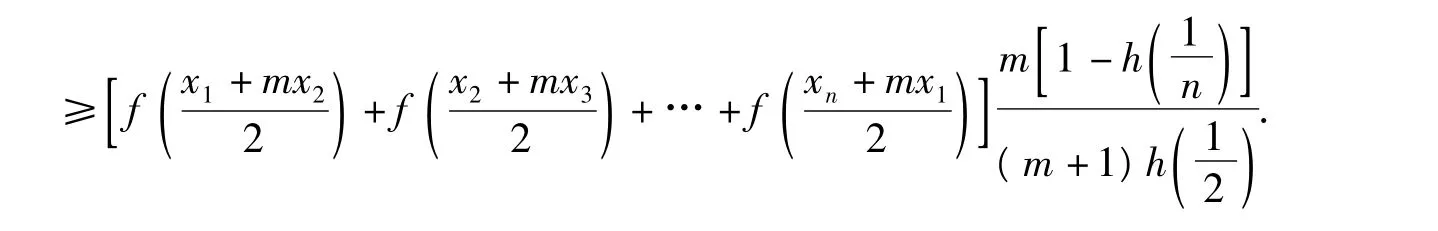
定理得证.

注3 当m=1，即f是h-凸函数，定理3即为文献［5］中的定理11.

则

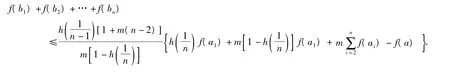
证明 因为f:［0，b］→R是(h-m)-凸函数，由推论1得

由(11)式得

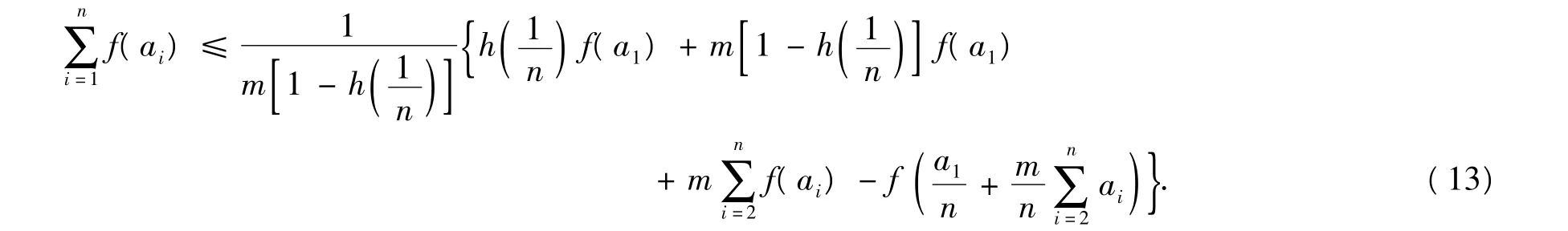
将(13)式代入(12)式得

定理得证.

注4 当m=1，即f是h-凸函数，定理4即为文献［5］中的定理12.

［1］Gill P M，Pearce C E M，Pecˇaric＇J.Hadamardıs inequality for r-convex functions［J］.J Math Anal Appl，1997，215(2): 461-470.

［2］Dragomir S S.On some new inequalities of Hermite-Hadamard type for m-convex functions［J］.Tamkang J Math，2002，33 (1):45-55.

［3］Bessenyei M，Páles Z.Hermite-Hadamard inequalities for generalized convex functions［J］.Aequationes Math，2005，69 (1-2):32-40.

［4］Varošanec S.On h-convexity［J］.J Math Anal Appl，2007，326(1):303-311.

［5］Latif M A.On some inequalities for h-convex functions［J］.Int J Math Anal，2010，4(30):1473-1482.

［6］Özdemir M E，Akdemir A O，Set E.On(h-m)-convexity and Hadamard-type inequalities［J/OL］.Math CA，2011.［2012-03-12］.http://arxiv.org/pdf/1103.6163v1.

Some Inequalities For(h-m)-Convex Functions

HUANG Jie，XU Xuan，ZHANG Yuhuai，YANG Yu
(School of Science and Technology，Zhejiang International Studies University，Hangzhou 310012，China)

This paper studies some inequalities for(h-m)-convex functions.By applying the method of analysis，four conclusions on the inequalities of(h-m)-convex functions are obtained.And the results extend to some related results in the relevant literature.

(h-m)-convex functions;inequality;supermultiplicative function

O178.1

A

2095-2074(2012)03-0080-05

2012-04-15

黄洁(1990-)，女，浙江绍兴人，浙江外国语学院科学技术学院数学系数学与应用数学专业2010级本科生;徐璇(1994-)，女，浙江台州人，浙江外国语学院科学技术学院数学系数学与应用数学专业2010级本科生;张宇槐(1992-)，男，浙江绍兴人，浙江外国语学院科学技术学院数学系数学与应用数学专业2010级本科生.

*通讯作者:杨瑜(1981-)，男，浙江安吉人，浙江外国语学院科学技术学院数学系副教授，理学博士.