二维依坐标(h-m)-凸函数的Hermite-Hadamard型不等式

张晓霞，王 杰，阮建苗

(浙江外国语学院科学技术学院，浙江杭州310012)

2008年Alomari等［11］考虑了f(x，y)为二维依坐标s-凸函数的情形，2009年Latif等［12］1653考虑了f (x，y)为二维依坐标h-凸函数的情形，即有

命题4 设f:Δ= a，[ ]b× c，[ ]d⊂0，[ )∞ × 0，[ )∞→R是Δ上的二维依坐标h-凸函数，且f∈L2(Δ)，h∈L1(［0，1］)，那么有

同理，令gx(y)=f(x，y)，则∀x∈ a，[ ]b，gx:c，[ ]d→R是 c，[ ]d上的(h-m)-凸函数，则有

二维依坐标(h-m)-凸函数的Hermite-Hadamard型不等式

张晓霞，王 杰，阮建苗*

(浙江外国语学院科学技术学院，浙江杭州310012)

建立了二维依坐标(h-m)-凸函数的Hermite-Hadamard型不等式，推广了二维依坐标凸函数、二维依坐标s-凸函数(第二种意义下)、二维依坐标m-凸函数与二维依坐标h-凸函数情形下的Hermite-Hadamard型不等式.

Hermite-Hadamard型不等式;凸函数;(h-m)-凸函数

1 引言及主要结果

1985年Toader①提出了m-凸函数的概念，2007年Varosanec［1］提出了h-凸函数的概念.h-凸函数是凸函数、s-凸函数、Godunova-Levin函数以及P-函数等函数类的推广，我们熟知这些函数类在数学的各个分支中有大量的应用，因此h-凸函数引起众多学者的兴趣与关注(见文献［2-4］等).2011年Ozdemir等［5］3进一步推广了h-凸函数与m-凸函数的概念，提出了(h-m)-凸函数的概念，即

定义1 设m∈(0，1］，函数h:［0，1］→(0，∞)，区间I⊂R，若函数f:I→R满足条件

其中x，y∈I，α∈ 0，[ ]1，则称f为I上的(h-m)-凸函数.

命题1［6］设f:R→R是一个凸函数，则对于任意的a，b∈R且a＜b，有

1999年Dragomir等［7］考虑了f为s-凸函数的情形，2002年Dragomir［8］又考虑了f为m-凸函数的情形，2008年Sarikay等［9］考虑了f为h-凸函数的情形，2011年Ozdemir等［5］4-6进一步考虑了f为(hm)-凸函数的情形，即有

命题2 设f是[ a，b]⊂[0 ，∞)上的(h-m)-凸函数，且f∈L1(［a，b］)，则有

与

与此同时，Hermite-Hadamard型不等式的高维推广也引起了广泛关注.2001年Dragomir［10］778考虑了二维依坐标凸函数情形下的Hermite-Hadamard型不等式，即有:

命题3 设f:Δ= a，[ ]b× c，[ ]d⊂0，[ )∞ × 0，[ )∞→R是Δ上的二维依坐标凸函数，那么有

2008年Alomari等［11］考虑了f(x，y)为二维依坐标s-凸函数的情形，2009年Latif等［12］1653考虑了f (x，y)为二维依坐标h-凸函数的情形，即有

命题4 设f:Δ= a，[ ]b× c，[ ]d⊂0，[ )∞ × 0，[ )∞→R是Δ上的二维依坐标h-凸函数，且f∈L2(Δ)，h∈L1(［0，1］)，那么有

2011年Ozdemir等［13］225考虑了f(x，y)为二维依坐标m-凸函数的情形，即有

命题5 设f:Δ= a，[ ]b× c，[ ]d⊂0，[ )∞ × 0，[ )∞→R是Δ上的二维依坐标m-凸函数，且m∈(0，1］，那么有

其中

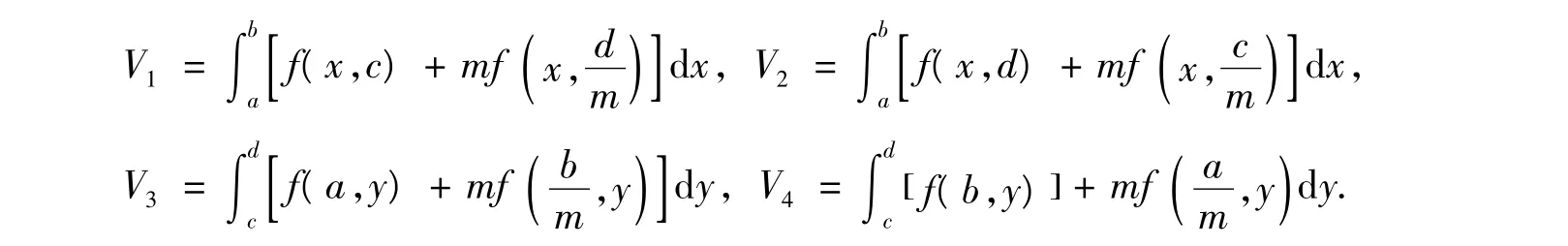
受上述文献的启发，本文的主要目的是建立二维依坐标(h-m)-凸函数的Hermite-Hadamard型不等式.

2009年Latif等［12］1651把h-凸函数的概念推广到二维空间，提出了二维h-凸函数与二维依坐标h-凸函数的概念，它们分别是二维凸函数、二维s-凸函数与二维依坐标凸函数、二维依坐标s-凸函数等概念的推广(详见文献［10］777，［14］).2011年Ozdemir等［13］222-223提出了二维m-凸函数与二维依坐标m-凸函数的概念.类似地，我们在本文中引进二维(h-m)-凸函数与二维依坐标(h-m)-凸函数的概念.

定义2 设函数f:Δ= a，[ ]b × c，[ ]d⊂0，[ )∞ × 0，[ )∞→R，函数h:0，[ ]1→0，[ )∞，且若∀α∈［0，1］，(x，y)，(z，w)∈Δ，有

其中m∈(0，1］，则称函数f是Δ上的二维(h-m)-凸函数.

定义3 设m∈(0，1］，函数f与h如定义2所述.若∀(x，y)∈Δ，单变量映射fy:［a，b］→R，fy(u)=f(u，y)和fx:［c，d］→R，fx(v)=f(x，v)都是(h-m)-凸函数，则称函数f是Δ上的二维依坐标(h-m)-凸函数.这等价于∀t，s∈［0，1］，(x，u)，(x，w)，(y，u)，(y，w)∈Δ，有

注1 容易证明，若f是Δ上的二维(h-m)-凸函数，则f必是Δ上的二维依坐标(h-m)-凸函数，且由文献［12］知，上述结论反之不真;

注2 若m=1，则二维依坐标(h-1)-凸函数即为二维依坐标h-凸函数;特别地，若h(α)∈{ α，αs}，则二维依坐标(h-1)-凸函数分别为二维依坐标凸函数与二维依坐标s-凸函数(在第二种意义下).若h(α)=α，则二维依坐标(α-m)-凸函数即为二维依坐标m-凸函数.

根据注1与注2，本文仅考虑f为二维依坐标(h-m)-凸函数的情形.我们的结论有:

定理1 设函数f:Δ= a，[ ]b× c，[ ]d⊂0，[ )∞ × 0，[ )∞→R是Δ上的二维依坐标(h-m)-凸函数，且若f∈L2(Δ)，h∈L1(［0，1］)，那么有

其中Vi(i=1，2，3，4)如命题5中所定义.

注3 特别地，若h(t)=t，则(1.7)式即为(1.6)式.

定理2 设函数f:Δ= a，[ ]b× c，[ ]d⊂0，[ )∞ × 0，[ )∞→R是Δ上的二维依坐标(h-m)-凸函数，f∈L2(Δ)，那么有

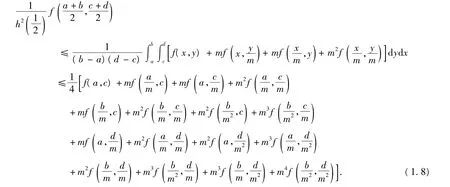
注4 若m=1，(1.8)式中的第一个不等式即(1.5)中的第一个不等式，而第二个不等式即为

特别地，若进一步有h(t)=t，则(1.8)式即为(1.4)式.

2 定理的证明

2.1 定理1的证明

证明 令gy(x)=f(x，y).因为f是Δ上的二维依坐标(h-m)-凸函数，则∀y∈ [ c，d]，gy: [ a，b]→R是 [ a，b]上的(h-m)-凸函数，由(1.2)式得

即

对(2.1)式两边同除以(d-c)，并关于y在 c，[ ]d上积分，得

同理，令gx(y)=f(x，y)，则∀x∈ a，[ ]b，gx:c，[ ]d→R是 c，[ ]d上的(h-m)-凸函数，则有

由(2.2)式与(2.3)式知，命题成立，即定理1得证.

2.2 定理2的证明

证明 令gy(x)=f(x，y).因为f是Δ上的二维依坐标(h-m)-凸函数，则∀y∈ [ c，d]，gy: [ a，b]→R是 [ a，b]上的(h-m)-凸函数，则由(1.3)式得

即

对(2.4)式两边同除以(d-c)，并对y在 c，[ ]d上积分，得

同理，令gx(y)=f(x，y)，则∀x∈ a，[ ]b，gx:c，[ ]d→R是 c，[ ]d上的(h-m)-凸函数，则有

同理，有

则由(2.7)与(2.8)式，得

同理可得

则把(2.10)、(2.11)式，以及(2.5)、(2.6)式中的第一个不等式代入(2.9)式，即得定理2的第一个不等式.

下面证明定理2的第二个不等式.类似地，对(2.6)式中的第二个不等式做估计，得

则由(2.12)式与(2.6)式中的第二个不等式，得

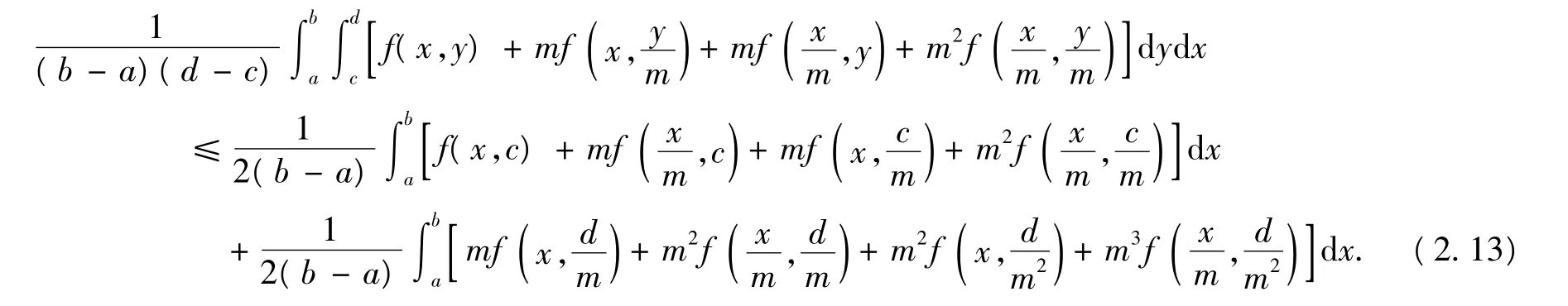
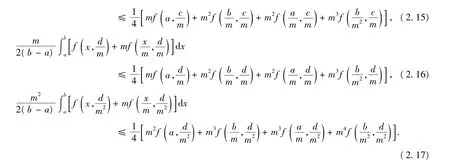
把(2.14)～(2.17)式代入(2.13)式即得定理2的第二个不等式.综上所述，命题得证.

注释:

①Toader G.Some generalization of the convexity.Proc Colloq Approx Opt.Cluj-Napoca［Romania］:University of Cluj-Napoca，Dept.of Mathematics，1985:329-338.

［1］Varosanec S.On h-convexity［J］.J Math Anal Appl，2007，326(1):303-311.

［2］Latif M A.On some inequalities for h-convex functions［J］.Int J of Math.Analy，2010，4(30):1473-1482.

［3］Burai P，Hazy A.On approximately h-convex functions［J］.J of Convex Analy，2011，18(2):447-454.

［4］Hazy A.Bernstein-Doetsch type results for h-convex functions［J］.Math Ineq Appl，2011，14(3):499-508.

［5］Özdemir M E，Akdemir A O，Set E.On(h-m)-convexity and Hadamard-type inequalities［J/OL］.Math CA，2011.［2011-12-15］.http://arxiv.org/pdf/1103.6163v1.

［6］Dragomir S S，Pearce C E M.Quasi-convex functions and Hadamard’s inequality［J］.Bull Austral Math Soc，1998，57 (3):377-385.

［7］Dragomir S S，Fitzpatrick S.The Hadamard’s inequality for s-convex functions in the second sense［J］.Demonstratio Math，1999，32(4):687-696.

［8］Dragomir S S.On some new inequalities of Hermite-Hadamard type for m-convex functions［J］.Tamkang J of Math，2002，33(1):45-55.

［9］Sarikaya M Z，Saglam A，Yildrim H.On some Hadamard-type inequalities for h-convex functions［J］.J Math Ineq，2008，2(3):335-341.

［10］Dragomir S S.On Hadamard’s inequality for convex functions on the co-ordinates in a rectangle from the plane［J］.Taiwanese J Math，2001，5(4).

［11］Alomari M，Darus M.The hadamard’s inequality for s-convex function of 2-variables on the co-ordinates［J］.Int J Math Anal，2008，2(13):629-638.

［12］Latif M A，Alomari M.On Hadamard-type inequalities for h-convex function on the co-ordinates［J］.Int J of Math Anal，2009，3(33).

［13］Özdemir M E，Set E，Sarikaya M Z.Some new hadamard type inequalities for co-ordinated m-convex and(α-m)-convex functions［J］.Hacettepe J Math and Statistics，2011，40(2).

［14］Alomari M，Darus M.Co-ordinates s-convex function in the first sense with some Hadamard-type inequalities［J］.Int J Contemp Math Sci，2008，3(30):1557-1567.

On Hermite-Hadamard Type Inequalities for(h-m)-Convex Functions on the Bi-dimensional Co-ordinates

ZHANG Xiaoxia，WANG Jie，RUAN Jianmiao
(School of Science and Technology，Zhejiang International Studies University，Hangzhou 310012，China)

The Hermite-Hadamard type inequalities for(h-m)-convex functions on the bi-dimensional co-ordinates is established in this paper，which are generalizations of the Hermite-Hadamard type inequalities for concex functions，s-convex fucntions(in the second sence)，m-convex functions and h-convex functions on the bi-dimensional co-ordinates.

Hermite-Hadamard type inequalities;convex functions;(h-m)-convex functions

O174

A

2095-2074(2012)03-0085-06

2012-03-20

国家自然科学基金项目(11101372)

张晓霞(1990-)，女，浙江金华人，浙江外国语学院科学技术学院数学系数学与应用数学专业2008级本科生;王杰(1989-)，男，浙江宁波人，浙江外国语学院科学技术学院数学系数学与应用数学专业2009级本科生.

*通讯作者:阮建苗(1979-)，男，浙江象山人，浙江外国语学院科学技术学院数学系讲师，理学博士.